如何实现功能需求的独立性：设计领域中的基本公理

在设计领域存在以下两个基本公理：

1.独立公理：保持功能需求（FR_S）的独立性

这意味着：理想情况下，每一个特定设计参数的改变应只影响一项功能，然而，实际上这是难以做到的，会出现许多耦合情况。然而了解这一公理，可以帮助人们识别耦合，并实施解耦设计。

至于FR_S究竟系独立或相关，全视所选的DP_S而定。但公理化设计所希望的是独立。如非独立，则有一套应对方式。独立公理阐明了功能要求与设计参数之间的关系。当有两个或两个以上的功能要求时，设计方案必须满足每一个功能要求，而且不影响其他的功能要求。这就要求选择设计参数时，既要满足功能要求，又要保持功能要求的相互独立。分析功能要求与对应的设计参数之间的关系，可以判断功能要求之间是否相互独立。在这里，应区别功能独立与物理部件独立，要求功能独立而并不是要求物理部件独立。换句话说，一个物理部件可能满足多个功能需求。还应指出，违反独立公理的设计，是不可能改进的。满足独立公理的设计不必进行传统意义上的优化。这时，最优化通常意味着在竞争的FRs中进行选择。

图3-3 易拉饮料罐

【案例3-1】易拉饮料罐设计

如图3-3所示易拉饮料罐，其功能是装一定容量的碳酸饮料。它需要满足多少FR_S？它有多少DP_S？有多少物理部件？

解：据铝制罐厂的专家说，易拉罐有12个FR_S，如承受轴向和径向的压力；抗从一定高度摔下的中等冲击；允许彼此在顶上摞起来；易拉开；用最少的铝；在表明上可印刷等。

为满足独立公理，必须至少有12个DP_S（有关定理见后续说明），如：罐体的厚度；罐底的曲率；罐头顶部和底部直径的减小（减少材料）；开片的波浪形（增加刚度）；开片的形状（易于摸到开片）等。但是，是否需要12个物理部件来对应满足12个DP_S呢？显然，可以将这些功能集成起来，实际上用三个部件即：罐体、盖子和开片。

设计区域的映射关系也可用下列设计方程来表达：

{FR}=（A）{DP} （3-1）

{DP}=（B）{P_V} （3-2）

式中 {FR}——设计目标（功能要求）的特征向量；

（A）——用以表征产品设计的设计矩阵；

{DP}——设计参数的特征向量；

（B）——用以表征过程设计的设计矩阵；

{P_V}——过程参数的特征向量。

按式（3-1），对于有三个FR_S和DP_S的设计，其设计矩阵为

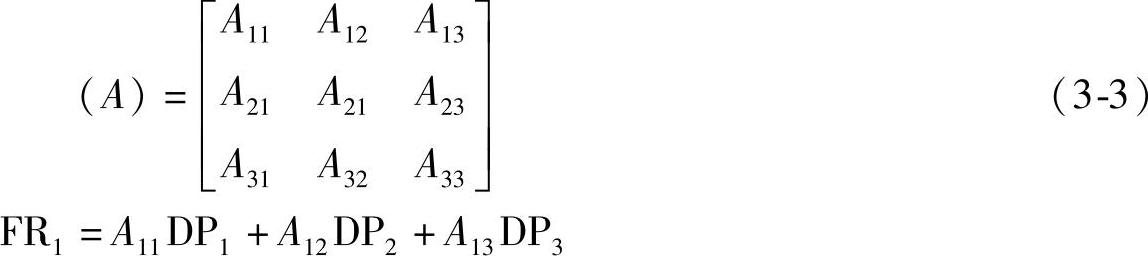
由此可得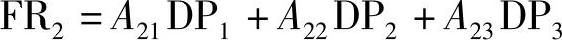

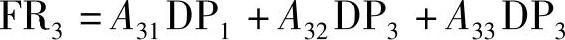
一般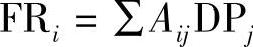

对于线性设计，A_ij是常数。对于非线性设计，A_ij是DP_S的函数。设计矩阵有两个特殊情况：对角线矩阵和三角形矩阵。在对角线矩阵中，除i=j外所有A_ij=0，，即

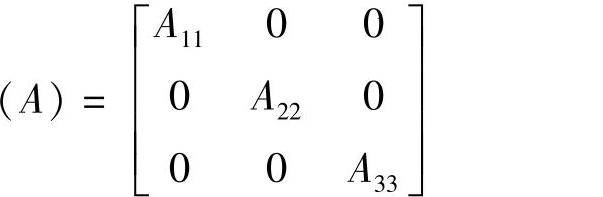
当（A）是对角线矩阵时，每一个FR可以用一个DP来满足，因而属于无耦合设计，是最理想的。

在三角形矩阵中，有两种情况：上或下三角形元素等于零，即

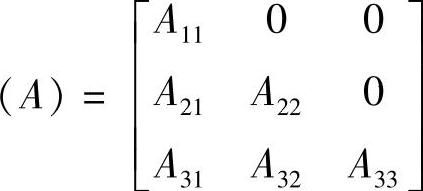
此为上三角形元素等于零。当（A）是三角形矩阵时，则可通过适当的顺序确定DP_S来保证FR_S独立性，从而实现解耦设计。这种情况可称为准耦合设计。

其他矩阵形式属于耦合设计，不满足独立公理。由此，为了满足独立公理，设计矩阵必须是对角线形或三角形的。

（1）理想设计 可以证明，当DPs的数目等于FRs的数目而且FRs始终保持彼此独立时，不会发生耦合设计，就是一个理想设计。(www.xing528.com)

（2）冗余设计 同样可以证明，当DPs的数目大于FPs的数目时，是一个冗余设计或者是一个耦合设计。

（3）耦合设计 同样可以证明，当DPs的数目小于FPs的数目时，总是得到一个耦合设计。

对于出现耦合设计的任何情况，都需要进行解耦设计。根据独立公理还可以证明，无耦合设计始终优于耦合设计。因此，必然存在一个无耦合设计或解耦设计，具有一个比耦合设计更小的信息含量。

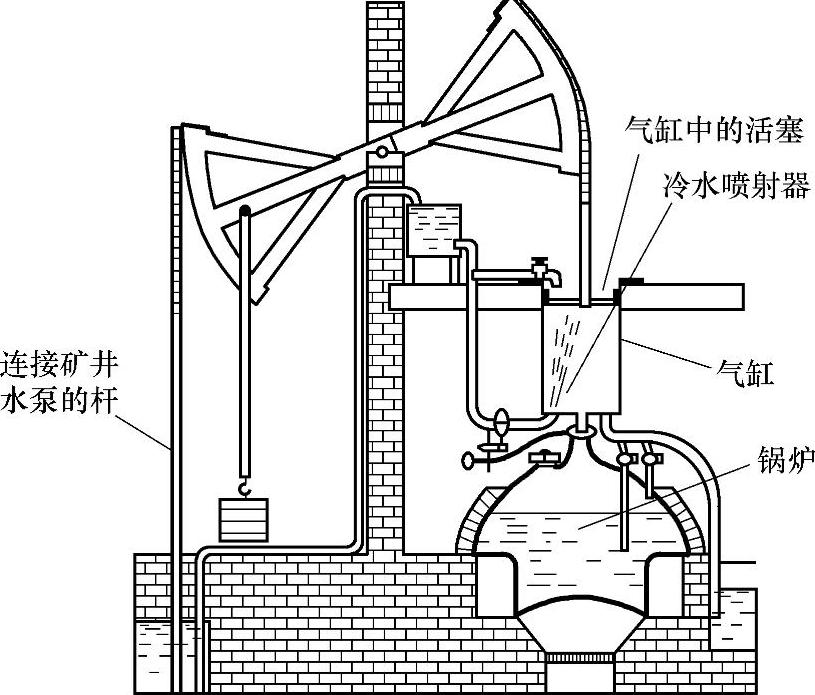
图3-4 牛顿蒸汽机简图

【案例3-2】蒸汽机的解耦设计

图3-4所示为牛顿蒸汽机简图，其工作原理为：蒸汽喷射到气缸里推动活塞向上运动，然后靠向气缸里喷射冷水时蒸汽冷凝，产生真空将活塞向下拉，从而形成往复运动，由活塞驱动连接矿井水泵的连杆把水从矿井里抽出去。由于锅炉、阀和蒸汽都会影响到蒸汽冷凝和活塞运动，且冷水喷雾会影响到活塞向上运动，蒸汽必须加热气缸，而冷水要冷却气缸和活塞。因此，这是一个不满足独立公理的耦合设计。后来，瓦特采用了分离的冷凝器，使之变为无耦合，又将单冲程改为二冲程，提高了效率。

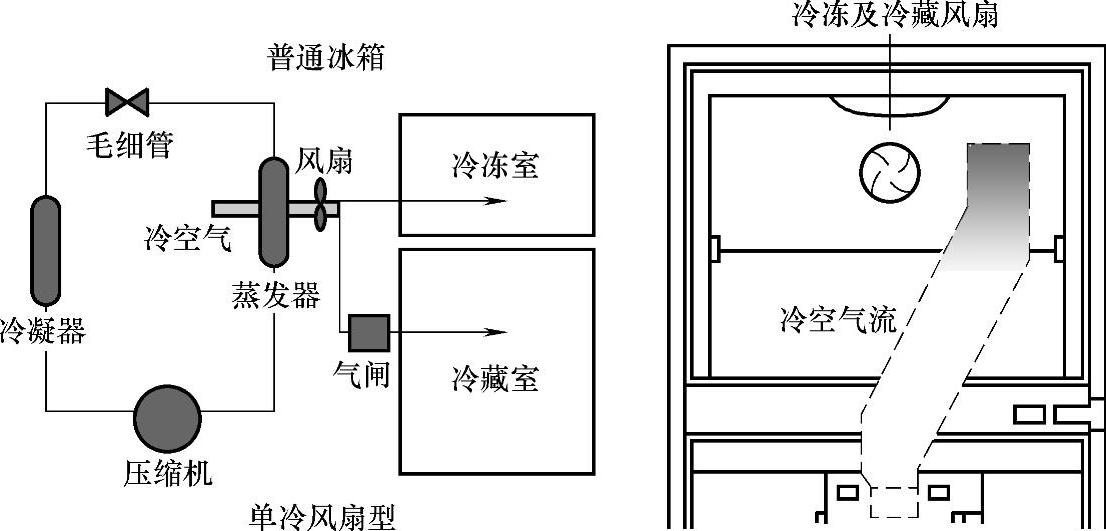
图3-5 普通冰箱

【案例3-3】冰箱设计

在图3-5和图3-6上列示了两种不同的冰箱设计方案。众所周知，冰箱分有冷冻和冷藏两个功能需求。前一个方案，冷冻和冷藏共享一个风扇。因此，冷藏区的温度不能相对冷冻区独立控制。这是一个耦合设计。后一个改进方案，采用了两个风扇，当冷藏区的温度高于设定值时，只需要增加的风扇工作即可，即使在压缩机停止工作期间冷凝器也可冷却进入冷藏区的空气。可以看出，这是一个满足独立公理的更好的设计。

2.信息公理：力求设计信息含量最少

该公理的核心是：最简单的设计，成功的可能性最大，是最好的选择。

一个给定F_i的信息含量I_i是由满足F_i的概率P_i定义的，即

如果在有m个FR_S的情况下，整个系统的信息含量就将上式中I_i换成I_sys即可。

当所有的FR_S不都是独立时，如出现耦合设计的情况下，P_m则等于满足所有的FR_S的条件概率的连乘积。

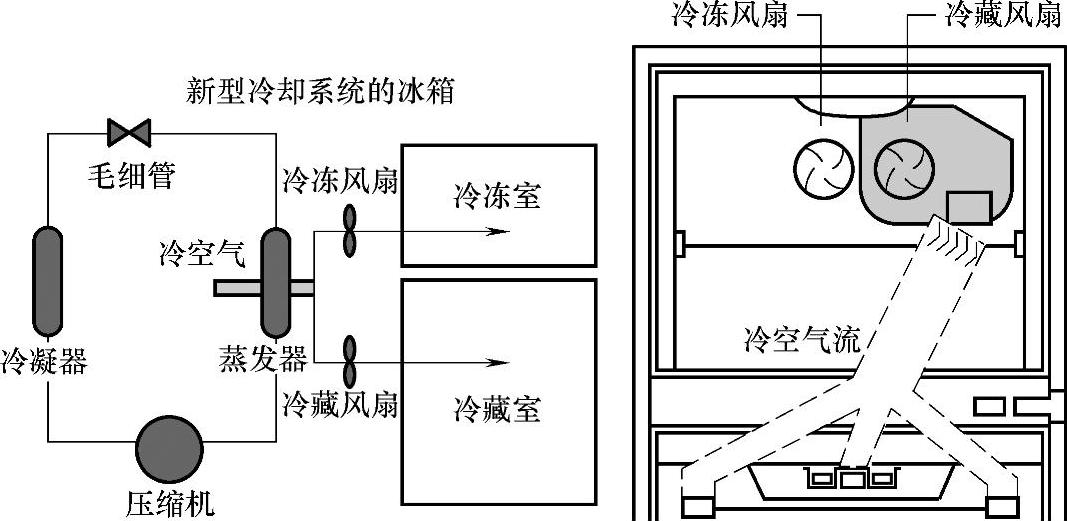
图3-6 新型冰箱

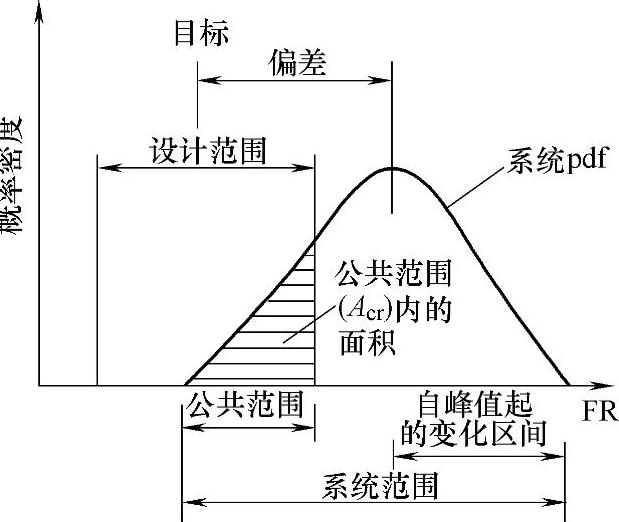
图3-7 功能需求的设计范围、系统范围和相应的概率密度函数

信息公理说的是，具有最小I的设计是最佳设计。因为这时为达到设计目标只需要最小的信息量。当所有的概率都为1.0时，信息量为零。反之，当概率之中的一个或几个等于零时，所需信息量就是无穷大。也就是说，如果概率很小，就必须提供更多的信息来满足功能需求FR_S。当成功概率低的时候，设计被称为复杂的；即满足FR_S所需的信息含量高。这种情况发生在一个产品的FR_S（或一个过程的DP_S）的公差小、精度要求高的时候。当部件数目增加时，某些零件不符合规定需要的可能性也就增加，故也可能出现这种情况。在一定意义上可以说，信息含量是复杂性的定量度量，因为复杂系统可能需要更多信息来实现系统功能。如果信息含量低，物理上的庞大的系统不一定复杂。反之，如果信息含量高，小系统也可能复杂。因此，复杂性与FR_S的设计范围紧密相关，设计范围越小，满足FR_S就越困难。成功概率可以由计算得到。图3-7提供了FR的设计范围、可以满足FR的系统范围和相应的概率密度函数（pdf）。设计范围和系统范围重叠的部分，就是能满足FR的区域，称为公共范围。其内的面积，就是设计成功的概率。

在所指定的FR上（带有公差范围），其对应的DP会有一定的概率可以满足这个FR。当达到这个带有一定公差范围FR的概率越高时，表示越有可能满足用户要求。因此，它是受到偏爱的，这符合信息公理。

信息公理表明在所有满足独立性公理的设计中，信息含量最少的设计是最佳设计，它是对设计方案进行评价的重要原则。根据信息公理的要求，在设计中应尽量简化设计工作，减少设计中各种因素的影响，以减少设计中产生功能耦合的可能性。由此可见，这两个公理是判断设计优劣的有力工具。

【案例3-4】定长切杆

问：若将杆A切到长度为（1+0.000001）m和杆B切到（1+0.1）m，哪一个成功的概率较高？如杆长从1m增加到30m，成功概率又将如何变化？

解：这取决于所用的切割设备。但对于有经验的工程师来说，切到高精度的会比较难，即切杆B比切杆A的成功概率高。

图3-8为手锯切杆的设计范围和系统pdf，系统范围取决于设计目标及其偏差，杆B的偏差较大，可使系统范围完全在设计范围内，因此，其成功概率为1。而杆A的切割精度要求极高，是手锯无法达到的，其成功概率为零。若杆长增加到30m则超出系统范围，其成功概率也为零。

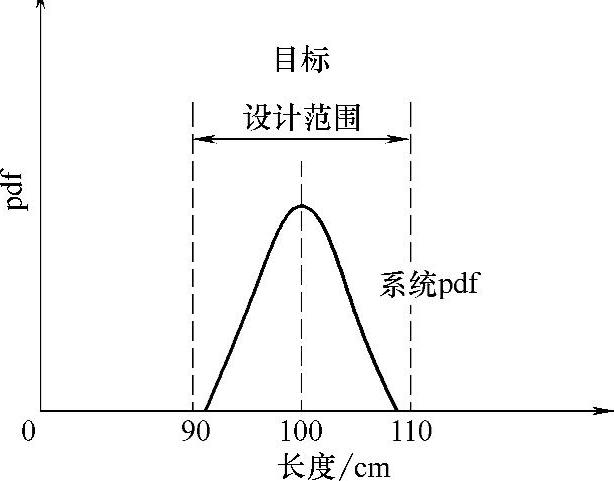
图3-8 手锯切杆的设计范围和系统pdf