电迁移理论解释液态镓薄膜的断裂现象

液态镓薄膜中观测到的断裂现象可以用电迁移理论来解释。众所周知，电迁移现象不仅会导致固态电路的失效［6］，还会在微流道中引起液态金属“流”［11］。考虑到液态金属的电磁性质与固态金属类似，首先假设电迁移现象也会引起液态金属电路的失效。

在电迁移过程中，离子受到如图2.5所示两个方向相反的力的作用［12，13］：

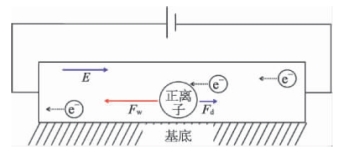
图2.5　电迁移示意［9］

（1）导电电子与离子实之间交换动量所引起的电子风力，Fw=ZweE，Zw是电迁移过程中与电子风力相关的有效化学价，e是元电荷，E是电场［13-17］。

（2）外加电场的直接静电力，Fd=ZdeE，Zd是电迁移过程中与静电力相关的有效化学价［18］。因而，离子实所受到的合力是上述两个力的总和，即Fem=Fw+Fd=Z*eE=Z*eρj，Z*=Zw+Zd是合力的有效化学价，j是电流密度，ρ是电阻率［19，20］。

除合力Fem之外，液态金属中的离子实还受到其他力的作用［18-20］。所有这些力都会对液态金属中的离子实流J产生贡献。因此，液态金属中的离子实的运动将服从如下修正的连续性方程［21-23］：

n是离子实密度，离子实质量流密度J=Jem+Jn+JT+Jp。J中各项的意义如下：

Jem=，是由电流密度j诱导的离子实质量流密度，D=μkT是扩散系数（液体的Einstein关系），μ是离子迁移率，k是Boltzmann常数，T是绝对温度；

Jn=-D▽n，是由离子密度梯度▽n诱导的离子实质量流密度；

JT=-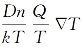，是由温度梯度▽T诱导的离子实质量流密度（Q是热扩散的热量）；

Jp=，是由压力梯度▽p诱导的离子实质量流密度（Ω是原子体积）。

方程（2.1）显示，如果流入一个区域的流密度大于流出该区域的离子流密度∂n/∂t＞0，那么▽·J＜0，于是材料就会在这个区域内堆积起来。但是，如果流入一个区域的离子流密度小于流出该区域的离子流密度∂n/∂t＜0，那么▽·J＞0，于是这个区域内就会形成空穴，这会引起电路的失效。只有当▽·J=0（或者∂n/∂t=0）时，电路才不会发生失效。这可以用来解释图2.2和图2.3中的实验结果。(www.xing528.com)

液态金属薄膜的断裂现象还有可能是由另一种现象引起的，即温度梯度。但是之前的测量已表明：保持薄膜两端为室温，而将薄膜中部的温度增至375℃时，薄膜并没有发生变化和断裂。这就排除了液态金属薄膜由温度梯度引起断裂的可能性。因而在下面的讨论过程中，将集中讨论电迁移的作用，忽略掉其他因素的影响，即假设Jem≠0，JT≈Jp≈Jn≈0。

此外，Ma等［9，10］还用另一种测量方法证明了液态金属薄膜的断裂现象是由电流j（或电子风力Fw）诱导的，而不是由外加电场E（或者直接静电力Fd）诱导的。具体来说，对样品施加一个电场E（或电压U），但保持电路为开路状态以保证电路中没有电流流过（即j=0）。结果显示，即使将电压升高到一个更高的值，也不会发生断裂现象。这可以用方程（2.1）来解释：如果j=0，那么▽·Je=0，从而有∂n/∂t=0。因而，离子实密度是一个常数，所以没有电迁移现象发生。

图2.4中的EDS能谱结果显示紧贴基片的残留物为氧化物，它们留在原处没有发生移动。这说明在基片上吸附的几个原子层中的电子风力Fw很小［11］。该现象可以这样来解释：由于镓及其合金需要利用氧化物来促进其与硅（或者玻璃）等基片之间的润湿能力［24，25］，所以液态金属薄膜与基片之间的薄层主要是氧化物Ga2O3；在电迁移过程中，上面的液态镓会被电子流推走，但下面的氧化物中没有电流流过，所以这一层氧化物不会受到电子风力Fw的作用，因而氧化物留在原处没有发生位移。

由于液态金属薄膜具有流动性，所以它比固态金属薄膜更容易受到电迁移现象的损害。这意味着电迁移现象可能会对打印电子电路、3D电子技术，以及其他相关微电子技术中使用的薄膜的可靠性产生很大影响，因而必须在这方面开展广泛而深入研究。

最后需要提及，除方程（2.1）以外，液态镓还应该服从如下两个修正的流体力学方程［9，10］：

（1）运动方程：参考一般形式的运动方程（Cauchy动量方程），并考虑合力Fem=Z*eρj的作用，容易得到如下描述液态金属包含电迁移效应的Navier-Stokes方程，

这里，v是流体的速度，p是液态金属内部的压强，η是第一黏滞系数，ζ是第二黏滞系数（或体黏滞系数）。

（2）能量方程：考虑能量守恒定律，可得到如下描述液态金属的能量方程，

其中，ε是单位质量内能，Ι是单位张量，τ是黏性应力，即

▽·（κ▽T）是从区域流出的热量，κ是热导。ρj2=E·j是电迁移过程中释放出的焦耳热（增加的热量）。

对上述方程的详细分析已超出了本书的研究范围，此处不再继续。