带隙型光子晶体光纤的特点与应用

带隙型光子晶体光纤是指由光子晶体阵列形成包层、中心缺陷形成纤芯，纤芯折射率低于包层的光纤。在带隙型光子晶体光纤中，光子晶体结构在一定波长范围内完全禁止光通过，即存在光子带隙。处于带隙的光场将被束缚在光纤中心向前传播，无法向四周扩散。低折射率纤芯使得传统全反射导光机制不再适用，而代以平面外带隙导光机制。带隙型光子晶体光纤完整波导特性可用有限元法求解式（3－3）获得。其中光子带隙特征可通过平面波展开法对包层光子晶体结构进行分析。

平面波展开法［72］是将模场以平面波的形式展开，将介电常数展开成傅里叶级数的形式，获得本征方程，求得光子晶体的能带结构。选择H作为分析对象，满足［72］

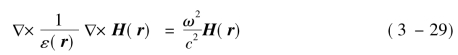
式中，ε（r）为光子晶体具有周期结构的介电常数分布。根据布洛赫理论，将H（r）表示为与光子晶体具有相同周期函数的平面波调制形式：

其中，表示波矢为k的磁场分量平面波两个正交偏振方向的单位矢量，满足形成右手螺旋系，满足=0；h（k，λ）表示的振幅。令f（r）=则f（r）也是周期函数，有

式中，G为光子晶体结构的倒格矢。

将式（3－30）和式（3－31）代入式（3－29）并化简，可获得本征方程：

不同光子晶体结构的f（G）具有不同形式，代入式（3－32）可以求解出不同能带结构，获得相应的带隙特征。Birks等［73］指出，利用石英玻璃和空气的折射率差，在含有面外波矢的情形下，就能够形成光子带隙结构，从理论上确认了光子带隙光纤的可行性。在光子带隙导光机制下，仿照阶跃光纤模式数目计算公式，可得到光子带隙光纤传输模式数目计算公式［74］：

式中，βL和βH分别为传输波长处对应的能带下限和上限。当NPBG＞1时，光子带隙光纤至少有一个传输模式。

带隙型光子晶体光纤中，空芯光纤是最具代表性结构的光纤。空芯光纤是指利用中心空气孔作为通道实现光传输的光纤。这种光纤理论上能够完全避免材料吸收损耗，实现无损传输。基于空气导光的独特优势，空芯光纤在高功率光纤激光器、高速信息传输、非线性光学和高灵敏传感器等领域展现出广阔的应用前景。目前已实现的空芯光纤主要包括空芯光子带隙光纤、Kagome光纤、布拉格光纤、负曲率光纤和Dirac光纤。此外，带隙型光子晶体光纤的最新研究热点之一是拓扑光纤。拓扑光纤革命性地实现光纤中光的单向传输和抗散射效应，有望进一步拓宽光纤的应用领域。

1.空芯光子带隙光纤

1991年，Russell［75］首次提出了空芯光子带隙光纤的概念。Birks等［73］在1995年建立了带隙导光机制，从理论上确认了光子带隙光纤的可行性。Knight等［76］在1998年成功拉制出光子带隙光纤，但该光纤纤芯仍是玻璃材料。1999年，Cregan等［74］成功拉制出第一根空芯光子带隙光纤，如图3－13a所示，实现了光场在空气中传输。

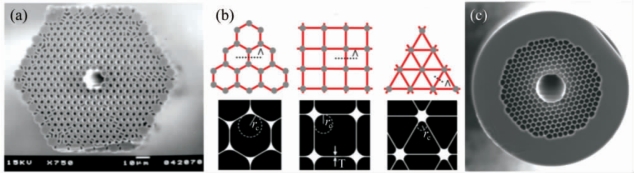
图3－13　空芯光子带隙光纤

（a）第一根空芯光子带隙光纤截面［74］；（b）孔洞三角形阵列、孔洞四方阵列和高折射率圆柱三角形阵列［82］；（c）19芯光子带隙光纤截面［84］

增加带隙宽度能够有效增加光子带隙光纤的传输带宽，相比于蜂窝结构，包层气孔为三角形阵列结构的光子晶体（见图3－13b），更容易实现光场在空气芯中传输［77］。Mortensen和Nielsen［78］指出，在包层气孔为三角形阵列的空芯光纤中，带隙宽度与空气填充因子f的平方成正比。Birks等［79］建立了光子晶体的紧束缚模型，解释了光子带隙光纤中带隙的形成机制。他们将能带近似为高折射率圆柱之间的超模，并参照布洛赫定理给出了束缚和反束缚情形下的边界条件，计算出能带的上下限。该模型解释了高空气填充因子和高折射率相对差能够增加带隙宽度的原理。Light等［80］设计包层气孔为三角形阵列结构的光子带隙光纤，在d/Λ=0.99时实现了相对带隙宽度W为33%。Poletti和Richardson［81］指出，包层气孔为四方阵列的光子带隙光纤，相比于三角形阵列结构，相对带隙宽度W提升为44%。Poletti［82］基于光子晶体中紧束缚模型指出，与高折射率圆柱相邻的圆柱数目越少，不同圆柱的耦合作用越弱，形成的能带越窄，带隙越宽。因此，他们设计了三角形阵列（高折射率圆柱）光子带隙光纤，在d/Λ=0.995时实现了相对带隙宽度W为66%。

传输损耗是空芯光纤的另一个重要参数。由于空气瑞利散射损耗仅为7×10－4 dB/km，是玻璃中瑞利散射损耗的1/200，因此空芯光纤是实现超低损耗光波导的重要候选方案。受限于制备工艺，第一根空芯光子带隙光纤［74］的传输损耗处于dB/cm的数量级。Smith等［83］改进了制备工艺，采用堆积热拉法制备了空芯光子带隙光纤（Λ=4.7μm，f=0.94，D=12.7μm），在1550 nm的损耗仅13 dB/km。他们还指出传输损耗的进一步降低受限于纤芯模式与包层模式的耦合效应。在光子带隙光纤中，包层中存在大量的表面模式。表面模的光场分布主要集中于包层的孔壁结构上，容易受到孔壁结构变形、不均匀和粗糙度等的影响，具有较大泄漏损耗。由于制备工艺和热张力作用，难以实现完美的孔壁结构。因此，需要降低基模能量在孔壁结构处的占比，改善空芯光子带隙光纤的传输损耗。增大纤芯直径能将更多的基模能量汇聚纤芯。Mangan等［84］通过扩大纤芯的缺陷孔，从移除中心7个原胞增加至移除中心19个原胞，如图3－13c所示，实现了1550 nm损耗为1.7 dB/km。另一方面，Correa课题组［85］通过直接移除中心7个原胞，去掉了填充中心大气孔的毛细孔，使与纤芯接触的孔壁结构的厚度只有包层中其它孔壁结构的一半，有效降低了基模能量在孔壁结构处的占比，实现了7芯光子带隙光纤最小传输损耗。

2.Kagome光纤

Kagome光纤指包层为Kagome光子晶体结构的空芯光纤。Kagome源于日语竹篮编制结构。这种光纤的纤芯是空气孔，包层为多层六芒星周期结构，气孔之间具有较薄的孔壁。2002年，Benabid等［86］率先制备出Kagome光纤，如图3－14a所示，并将其用于氢气受激拉曼实验。2006年，Couny等［87］指出，Kagome光纤相比于空芯光子带隙光纤，具有传输损耗小的优点。由于传输带宽大，Kagome光纤可选用较大气孔间隔（Λ约为普通空芯光子带隙光纤气孔间隔的6倍），从而降低制备难度。

图3－14　Kagome光纤(www.xing528.com)

（a）第一根Kagome光纤截面［86］；（b）内摆线形Kagome光纤截面［91］

Kagome光纤不具备完整的光子带隙结构，其导光机制与光子带隙光纤不同。学者还在研究其导光机制，目前尚无定论，主流的观点是低包层态密度理论。光子态密度是指光子晶体在特定频率下支持的模式数目。Hedley等［88］指出，Kagome光纤的传输通带与Kagome光子晶体的低光子态区重合，相对于Kagome光纤，其纤芯模式径向相位变化缓慢，而包层模式径向相位快速振荡。因此，尽管在相同频率下同时存在纤芯模式与包层模式，但两者横向波矢严重失配，无法发生耦合作用［89］。

受限于制备工艺，第一根Kagome光纤［86］在3501700 nm波长范围内损耗为3 dB/m。Wang等［90］指出，将Kagome光纤的纤芯由圆形变换为内摆线形，能够有效减小基模与包层模式的重叠程度，光纤损耗减至0.18 dB/m，工作波长为8501750 nm。Debord等［91］指出，增加内摆线形孔壁的曲率，如图3－14b所示，能够有效降低损耗，并在1064 nm制备出损耗为17 dB/km的Kagome光纤。Wheeler等［92］在此基础上，制备了1550 nm最低损耗为13.9 dB/km的Kagome光纤。

3.布拉格光纤

布拉格光纤由百微米量级空芯纤芯和径向方向呈高、低折射率周期性变化的一维光子晶体包层组成。早在1978年，Yeh等［93］就提出布拉格光纤的概念，并基于传输矩阵法进行相应理论分析。1998年，Fink等［94］制备了布拉格光纤，并指出该光纤在一定波长范围内可将任意入射方向和任意偏振方向光波约束在空气纤芯中，实现低损耗传输。2002年，Temelkuran等［95］利用As2Se3和聚醚砜（polyethersulfone，PES）高分子材料制备径向周期性结构的布拉格光纤，如图3－15所示，在7.510.6μm波长范围内实现低于1dB/m的损耗。该损耗值远小于包层材料的本征吸收值（As2Se3：约7 dB/m；PES高分子材料：约100000 dB/m）。Vienne等［96］利用石英玻璃，制备了近红外波段布拉格光纤。该光纤包层为四层气孔阵列，环状壁和环状排布的气孔形成了径向周期结构，工作波长为7501700 nm，在1400 nm的损耗为1.5 dB/m。为了进一步降低光纤损耗和拓宽传输带宽，Husakou和Herrmann［97］采用遗传算法，不同材料采用不同厚度，将低损耗传输窗口拓宽为5921383 nm，损耗将低至dB/m的数量级。Hu等［98］指出，包层中相邻两层材料的厚度比对传输窗口具有重要影响。他们通过厚度随半径增加而增加的复合准周期包层结构将传输窗口拓宽两倍，实现TE01模式在8101700 nm范围内损耗小于100 dB/m。Shang等［99，100］通过将径向单周期内双层结构替换成三层夹心结构，在35μm范围内实现HE11模式小于0.01 dB/m低损耗传输。另一方面，Ozturk等［101］通过在轴向方向上引入锥形结构，对不同周期常数的传输窗口取交集，实现了10.512.5μm窄带传输。

图3－15　布拉格光纤［95］

（a）布拉格光纤截面；（b）包层的布拉格周期结构

4.负曲率光纤

负曲率光纤指纤芯轮廓为负曲率结构的光纤，通常由中心缺陷气孔和环绕纤芯的单层微管构成。受低损耗内摆线形Kagome光纤启发，Pryamikov等［102］在2011年首次提出并制备出负曲率石英玻璃光纤，如图3－16a所示。负曲率光纤具有低损耗、低弯曲损耗、宽传输窗口和结构简单等优势。Yu和Knight［103］将纤芯周围的圆柱微管替换成“冰淇淋”状微管，并减小管壁厚度，实现8004500 nm内低损耗传输，最低损耗值为24.4 dB/km@2400 nm。Kolyadin等［104］指出圆柱微管之间接触点将会导致谐振，增加损耗。他们通过在圆柱微管之间引入间隙，如图3－16b所示，实现了2.57.9μm激光传输，传输损耗约为50 dB/km@3.39μm。Belardi和Knight［105］进一步移除接触点来降低光纤的弯曲损耗，在3.35μm实现了0.25 dB/r的弯曲损耗，弯曲半径为2.5 cm。Poletti［106］提出在包层圆柱微管中进行复合设计，如在圆柱微管中嵌套一个更小直径的微管，能进一步降低光纤损耗。Hasan等［107］在圆柱微管中嵌套一个椭圆柱管，实现9001800 nm低损耗传输和更小的弯曲损耗。Gao等［108］将单个圆柱微管替换成两个圆柱串联的微管结构，如图3－16c所示，在1550 nm实现了2 dB/km的最低传输损耗和1 dB/r的弯曲损耗，弯曲半径为10 cm。

图3－16　负曲率光纤

（a）负曲率光纤截面［102］；（b）无接触点的负曲率光纤截面［104］；（c）无接触点的复合结构负曲率光纤截面［108］

5.Dirac光纤

Dirac光纤是指利用包层光子晶体能带中Dirac点，而不是带隙，进行光场传输的光纤。Dirac点是能带结构中具有线性能量－波矢关系的交汇点，如图3－17b所示。2015年，Xie等［109］首次提出Dirac光纤，并指出Dirac光纤模式在横截面上具有独特的电磁场幂律衰减形式，实现光场与包层材料的长程相互作用。通过优化二维三角晶格光子晶体结构，增大Kz分量，使Dirac频率在第一布里渊区内只存在单个模场分布，避免纤芯模式与包层其它光子晶体模式发生耦合。Xie等［109］指出空芯三角晶格光纤中Dirac点需要高折射率差才能实现。Yang等［110］提出增大填充因子能够放宽Dirac点形成条件，并通过改进蜂窝晶格结构，如图3－17c所示，制备出石英玻璃Dirac光纤。

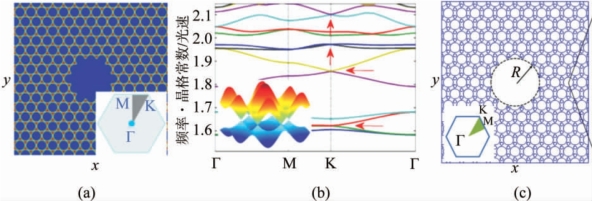
图3－17　Dirac光纤

（a）Dirac光纤截面［109］；（b）光纤能带中的Dirac锥结构［109］；（c）改进蜂窝晶格结构的Dirac光纤截面［110］

6.拓扑光纤

拓扑光纤，即具备拓扑结构和拓扑效应的光纤。在晶体中，拓扑学主要研究能带结构中不受局部缺陷影响的整体特性。2018年，Lu等［111］首次在理论上提出单向传输的拓扑光纤，通过螺旋调制三维外尔拓扑光子晶体使其在纤芯处形成轴向线缺陷结构，利用沿着线缺陷单向传输的拓扑态作为光纤模式。如图3－18a所示，拓扑光纤模式能够绕过纤芯中心的金属小球，无反射地往前传输。Pilozzi等［112］基于一维拓扑链结构理论设计了环形结构的拓扑光纤，如图3－18b所示。该光纤具有低折射率材料与高折射率材料依次间隔排列的多个同心环结构，不同环厚度满足Aubry－Andre－Harper（AAH）模型调制条件。

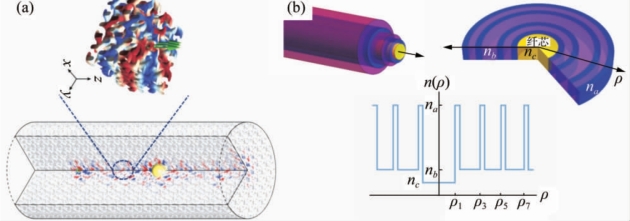
图3－18　拓扑光纤

（a）单向传输的拓扑光纤示意图［111］；（b）AAH调制的拓扑光纤［112］

目前，拓扑光纤在制备上还存在一些基础问题有待解决，包括简化拓扑光纤结构以兼容于现有光纤制备技术，利用低折射率材料实现拓扑带隙等。