环形结构光纤：稳定传输OAM模式的新趋势

在芯层与包层之间引入一层更高折射率的环层结构，将光波束缚在环形区域内，这种结构光纤称为环形结构光纤，其横截面结构如图3－8所示。其中a1是环层的内半径，a2是环层的外半径。

环形结构光纤最初于20世纪70年代被提出［39］。假设环形结构光纤具有阶跃折射率分布，从光纤传导模式动量守恒出发，可得［40］：

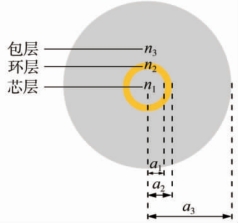
图3－8　环形结构光纤

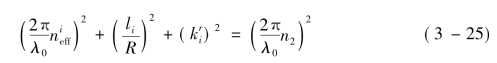
式中，为第i阶传导模式的有效折射率；R为环层的平均半径［R=（a1+a2）/2］。式（3－25）等号右侧代表模式总动量，左侧分别代表第i阶传导模式的纵向、角向和径向动量。其中模式的径向动量与环层厚度w有关（w=a2－a1）。合理控制w值，可使环形结构光纤只支持径向一阶模式，此时所有传导模式可以看成具有相同径向动量；但该径向动量的大小仍然受w影响，相对较大的w可使所有的径向一阶模式具有较小的径向动量。因而在径向一阶模式限制之下，相对较大w可使所有传导模式的neff更加接近环层最高折射率n2。

径向一阶模式限制下，环形结构光纤中相邻模式之间有效折射率差（Δneff）为

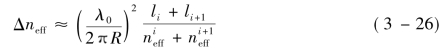
式中，分别表示li阶和li+1阶模式的有效折射率。由式（3－26）可知：环形结构光纤中相邻模式之间Δneff随着角向阶数的增加而增大，其耦合随之降低。另外，假设相对折射率差Δ21=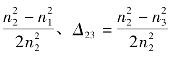不变的情况下，R增加会导致环形结构光纤支持的传导模式增加，从而降低模之间的Δneff。

环形结构光纤的环层平均半径R、环层厚度w以及环层和包层相对折射率差对传输特性具有重要影响，这也决定了其主要的应用场景。目前已报道的环形结构光纤可分为两类：(www.xing528.com)

第一类为轨道角动量（orbital angular momentum，OAM）光纤。环形结构光纤的径向限制使其可稳定传输OAM模式，因此被称为OAM光纤。由一阶微扰理论，光纤径向较大的折射率梯度可引起近似简并的EH、HE本征模式分离，增大Δneff。由此，同一模式中自旋－轨道旋转方向一致以及相反的OAM模式进一步分离，保持低串扰。由于EH、HE本征模式之间的分离，OAM光纤通信系统无法使用现有LP模式复用系统，只能重新构建OAM模式兼容的编码和解码模块，并采用多进多出（multiple－input multiple－output，MIMO）均衡模块完成通信过程。

目前，针对此类OAM光纤的设计主要从改变环层径向折射率分布和增大环层与包层折射率差两方面入手。前者代表性工作是加拿大Laval大学的Ung等［41，42］提出具有反抛物线渐变折射率分布的环形结构光纤，如图3－9a所示。此类环形结构光纤在保证近似径向一阶折射率分布的同时，可在环层与包层界面处实现最大的折射率差，从而实现OAM模式的进一步分离。后者代表性工作是美国波士顿大学Gregg等［43］提出的空心环形结构光纤，如图3－9b所示，较大空气芯层和环层折射率差不仅有助于分离OAM模式，还可以支持更多OAM传导模式。

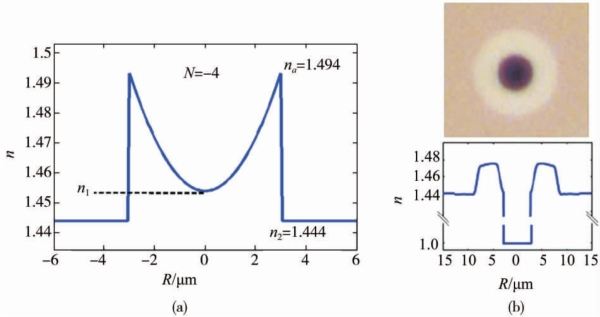
图3－9　OAM环形结构光纤设计

（a）反抛物线渐变折射率分布的环形结构光纤［41］；（b）空心环形结构光纤［43］

第二类为增加模式简并度的环形结构光纤。与OAM光纤设计理念相反，此类光纤主要通过降低径向折射率梯度来增加模式的简并度，使它们之间达到强耦合状态，以降低模式时延；同时拉大模式间的Δneff，以减小模间串扰。此类设计主要应用于几十千米量级的传输系统，既可用于基于相干检测的模分复用系统中，也可用于直接检测的模组复用系统中，且LP和OAM模式在此类系统中具有类似的传输性能。如前所述，由于环形结构光纤限制径向高阶模式，各高阶模组具有固定的模式数，因此在相干模分复用系统（mode division multiplexing，MDM）中，仅采用复杂度较低的4×4 MIMO即可实现环形结构光纤高阶组内模式均衡；同时模组复用系统也避免了接收端复杂度随模组阶数升高而增加的问题，因而具有较高的高阶模式拓展性。

目前，此类光纤最具代表性研究工作之一的是中山大学Zhang等［44］提出的渐变折射率环形结构光纤。他们通过对环层进行折射率渐变设计，降低光纤径向折射率变化梯度，使光纤可以在较高Δ21和Δ23时，实现模式的低时延。此类光纤最高可支持5阶OAM模式。但由于Δ21和Δ23较大，该光纤具有较大损耗，约为0.75 dB/km。另外，英国南安普顿大学Jung等［45］提出具有较低Δ21和Δ23的阶跃折射率环形结构光纤，如图3－10所示，该光纤支持的传导模式数目减少，但更易于制备，并且损耗大大降低（不超过0.32 dB/km）。

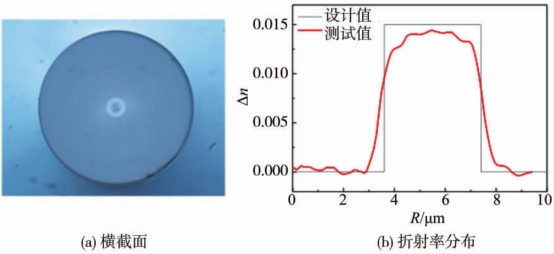
图3－10　阶跃折射率分布的环形结构光纤［45］