光纤的模式特征及相关参数详解

上节光纤中的传输光场：

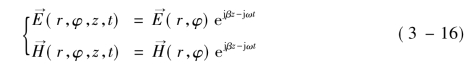
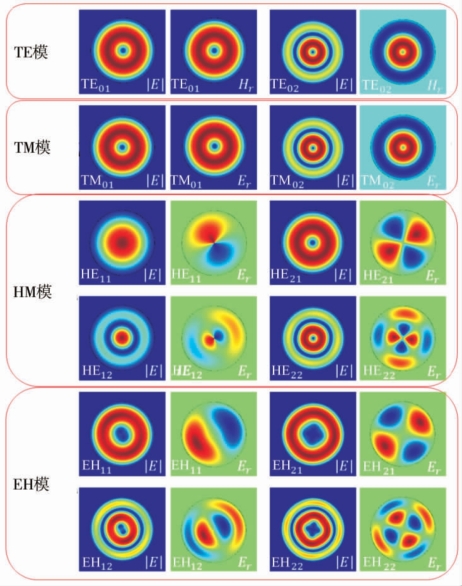
式中，为电磁场的横向分布。电磁场的六个分量均在横截面具有横向分布，并且这些分量之间必须满足式（3－4）。一组具有特定分布的电磁场，称为一个横模。横模的六个分量将以相同速度向前传播，传播常数为β。通过求解该横模的特征方程可以获得β的值。光纤中存在多个不同分布的横模，主要分为四类：横电模（TE）、横磁模（TM）、磁电模（HE）和电磁模（EH）［1，2］。对于TE模，Ez=Er=Hφ=0；对于TM模，Hz=Hr=Eφ=0；对于HE模和EH模，六个电磁场分量均为非零，也称为混合模式。光纤中模式可通过角向分布（下角标υ）和径向分布（下角标m）组合而成。υ的物理意义是任一非零电磁场分量，绕圆周一圈，获得的场强极大值数目。由式（3－14）和式（3－15），对于TE模和TM模，υ=0。m的物理意义是任一非零电磁场分量，从纤芯沿径向方向至无穷远处，获得的场强极值数目。图3－1中给出了光纤中一些横模的模场分布。

在光纤中，纤芯模式的β需要满足［1，2］：n2 k0≤β≤n1 k0。若β≤n2 k0，则模式在包层中传输，称为泄漏模。β=n2k0为临界状态，此时，W=0及U=Vc，Vc称为归一化截止频率。在光纤中，随着频率的增加，纤芯传播模式会逐渐转变为包层中泄漏模。定义模式转化的临界频率为截止频率νc，有νc=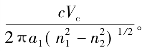可以证明，光纤中基模HE11的截止频率为νc=0，即基模不会被截止，总会在纤芯中传播。光纤中二阶模式的截止频率为νc=2.405。因此，若νc＜2.405，纤芯中只有基模可以传输，称为单模工作条件。基于单模工作条件，可以得到单模半径a1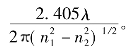＜根据纤芯模式的β，定义模式等效折射率neff=β/k0，能够为光纤与器件设计提供参考。

(www.xing528.com)

图3－1　光纤中各类横模的模场分布

由式（3－12）式（3－15），光纤中模式一般为混合偏振模式，并且横截面不同位置处光场偏振方向不同。特殊地，对于基模HE11，可得到线偏振态的偶模（Ex≠0，Ey=0）或线偏振态的奇模（Ex=0，Ey≠0）。因此，光纤中基模可以是线偏振态。对于TE模式（Er=0，Eφ≠0）和TM模式（Er≠0，Eφ=0），分别为角向偏振模式和径向偏振模式。在自由空间中，通过叠加两个偏振光束并控制相应的时延，可实现任意偏振态，包括不同角度的线偏振光、左/右旋椭圆偏振光和左/右旋圆偏振光。光纤中光场偏振态也可以通过光场叠加实现。例如，通过基模偶模和奇模的线性组合，可以在光纤中获得不同角度的线偏振光、左/右旋椭圆偏振光和左/右旋圆偏振光；HEν+1，m模和EHν－1，m模的线性组合，可得到水平和垂直方向上线偏振光；TE模式和TM模式的叠加态，或任一高阶光束偶模和奇模的叠加态，可实现左/右旋椭圆偏振光和左/右旋圆偏振光。左/右旋椭圆偏振光在光纤横截面不同位置处光场的椭偏率和旋角可以不同，但光场的旋转方向一致。

光纤中，若两个模式满足同一本征方程，并且具有相同的色散特性和截止频率，则两个模式简并。光纤中任意模式的奇模和偶模即为正交简并模式。特殊地，若光纤满足弱波导近似［1，2］，即则可以对特征方程（3－9）进行化简，获得三组简并模式。第一种，HE1m的偶模和奇模；第二种，TE0m模、HE2m的偶模和奇模、TM0m模；第三种，HEν+1，m的偶模和奇模、EHν－1，m的偶模和奇模。简并态模式具有相同的传播常数，因此光场可以任意叠加。更进一步地，TE0m模、HE2m的偶模和奇模以及TM0m模的任意两个模式（HEν+1，m的偶模和EHν－1，m的奇模，或者HEν+1，m的奇模和EHν－1，m的偶模）特定比例的叠加态，可以实现线偏振的模场分布。因此，把弱波导模式也称为线偏振模式（linearly polarized mode，LP），表示为LP0m、LP1m和LPlm模式，光斑模式为花瓣状。其中，l为角向模式阶数，物理意义是绕圆一周，模式光强极值数目的一半；m的物理意义是从纤芯沿径向方向至无穷远处，模式光强的极值数目。

通过调控光纤结构，可以改变传播常数。定义模式振幅最大点的传播速度为模式的群速度，其中η为纤芯中的能量占比值。群速度决定了该模式能量的传播速度。对于两根并排光纤波导，若存在两个β相近并分别位于两个并排光纤中的任意模式，则这两个模式将以近似相等的速度往前传播，模式之间的作用时间将被充分地延长。在微扰（制备缺陷或环境扰动引起）作用下，该两个模式能够进行能量交换，即产生耦合现象。对于同一根光纤，若不同模式的β不同，将导致色散现象。具体地，光纤中色散可以分为材料色散、波导色散、偏振模色散和模间色散四种。材料色散是由于材料折射率随波长而发生变化，使得不同波长的光波传输速度不同而导致的色散。波导色散由波导结构所决定，计算公式为Dw（λ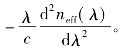）=偏振模色散是由光纤制备过程的缺陷、外部扰动（例如应力等）或者设计的特殊结构导致的圆双折射效应，使得左旋光和右旋光的传播速度不同。模间色散，是由不同阶模式传输速度不同引起的。

光纤中非线性效应对模式也存在影响，能量守恒决定了参与非线性作用模式的频率，而动量守恒则决定了模式的阶数和传播常数。动量守恒即相位匹配条件，要求参与非线性作用的模式波矢之间满足等式关系。而光纤中模式波矢，其横向分量由模式阶数决定，纵向分量由模式传播常数决定。因此，相位匹配条件实际上就是模式阶数和传播常数匹配的过程。光纤中不同模式的非线性系数不同，计算公式为γ=。其中，γ2为材料的非线性系数，ω为角频率，c为真空中的光速，Aeff为模式等效面积，定义为Aeff=