熔池流场与热场的数值计算

焊接过程中，液态熔池的表面是自由表面。作用于熔池表面的力有电弧压力、表面张力、熔池重力等。在GMAW焊接时，还有熔滴的冲击力。在各种力的共同作用下，熔池表面产生三维变形，尤其是工件熔透之后，焊接熔池的正面和背面都产生明显的变形。熔池表面的凹凸变形影响到了电弧的行为，改变了熔池内的传热条件，熔池的三维形状随之要发生变化，从而影响到焊接的质量和效率。因此，熔池流场和热场的数值计算首先要考虑熔池自由表面的变形与界面追踪。目前，熔池自由界面的追踪方法有坐标变换法和VOF法等。

1.TIG焊熔池的自由表面变形

熔池上表面的形状用z＝φ（x，y）表示。在图2-20所示的坐标系下，φ（x，y）应满足方程：

2y）φxx－2φxφyφxy＋（1＋φ2

式中p_a——电弧压力（Pa）；

ρ——液态金属的密度（kg／m³）；

g——重力加速度（m／s²）；

γ——表面张力系数（N／m）；

C₁——待定常数（Pa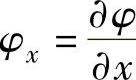）。，φ，，，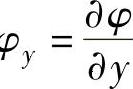

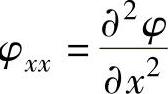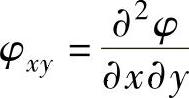
在工件上表面熔池以外的位置，φ（x，y）＝0。在不填充焊丝的情况下，由于变形前后熔池金属的总体积不变，因此熔池上表面的形状函数φ（x，y）满足以下约束条件：

式中Ω₁——工件上表面的熔池区。

图2-20 TIG焊熔池表面变形示意图

a）未熔透 b）全熔透

如图2-20b所示，当工件熔透以后，熔池的上、下表面将同时产生变形。设熔池的上、下表面形状方程分别为：z＝φ（x，y）、z＝ψ（x，y），其表面变形的坐标原点分别位于工件上、下表面。熔透后熔池上表面形状方程满足以下方程：

熔透后熔池下表面形状满足以下方程：

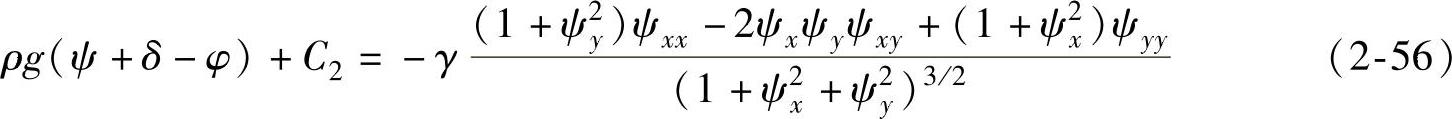
式中δ——工件的厚度；

C₂——待定常数。

同样遵循变形前后熔池内金属总体积不变的原则，以上两式必须满足以下约束条件：

其中，Ω₁、Ω₂分别为熔池区的上、下表面。如果点（x，y）在熔池区以外，则有φ（x，y）＝0，ψ（x，y）＝0。

电弧压力可表示为

式中r——任一点到电弧中心的距离（m），；

μ_m——真空磁导率（H／m）；

I——焊接电流（A）；

σ_j——电流分布参数（m）；

v₀——焊接速度（m／s）；

t——时间（s）。

2.贴体坐标系下控制方程组的形式

在焊接过程中，当熔池的表面要发生变形时，由于熔池的运动，工件上计算区域的形状随着电弧的运动而不断变化。控制方程组式（2-48）～式（2-52）是在直角坐标下推导出来的。有限差分法非常适合于规则的平面边界。但是熔池的自由表面产生变形后，熔池上、下表面的平面边界不再存在，形成三维空间曲面。如果此时仍然在直角坐标下处理该空间曲面，就会产生一个能量边界条件非常复杂的锯齿形边界，很难进行计算和处理。

为了更好地反映焊接过程中出现的熔池表面变形，并且更好地处理熔池的上、下曲面边界，使得各坐标和所计算工件的边界一一对应，采用了适合于熔池表面变形的贴体坐标系，如图2-21所示。贴体坐标系（x∗，y∗，z∗）和原直角坐标系（x，y，z）的转换关系是

x∗＝x（2-59）(www.xing528.com)

y∗＝y（2-60）

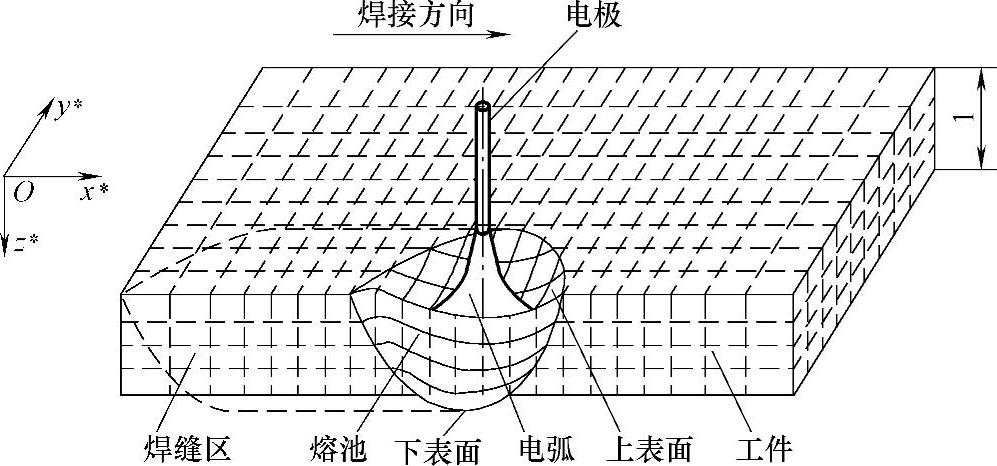
图2-21 贴体坐标系下的网格系统示意图

显然，在熔池的上表面z＝φ处，z∗＝0；而在熔池的下表面z＝δ＋ψ处，z∗＝1。通过该代数变换，不仅将直角坐标系下不规则的物理空间转变为非正交贴体坐标系下规则的计算空间，使坐标轴与计算区域的边界相一致，而且使得模拟的过程更加符合实际。

3.贴体坐标系下控制方程组的定解条件

（1）能量边界条件 在图2-21中，焊接工件的上表面受到电弧的加热，并将热量传递到工件内部去。同时也以对流、辐射和蒸发的方式把部分热量传递给周围的介质。在工件的其他表面也存在着辐射传热。同直角坐标系中的能量边界条件相比较，贴体坐标系中的热能边界条件只在工件的上下表面发生变化。

焊接电弧把热能传给工件是通过工件上一定的作用面积进行的。一般用高斯函数来描述电弧作用于平面工件的热流密度分布。但是，根据高斯电弧热流分布计算出的熔池上表面形状的后拖不足，呈扁圆状。为了克服这一不足，可采用双椭圆型热流密度分布函数。

关于工件上表面散热损失的对流热流密度、辐射热流密度和蒸发热流密度，其表达式分别为

q_c＝α_c（T－T_f）（2-62）

q_r＝σ_sε（T⁴－T_f⁴）（2-63）

q_e＝W_qL_q（2-64）

式中α_c——工件与环境的换热系数［W／（m²·K）］；

σ_s——Stefan-Boltzmann常数［W／（m²·K⁴）］；

ε——表面辐射系数；

L_q——液_-气相变潜热（J／kg）；

T_f——环境温度（K）；

W_q——蒸发率［kg／（m²·s）］。

蒸发热损失只存在于熔池区，与温度有关。对于钢：

因此，贴体坐标系下工件上表面热流密度的净输入为

对称面（y＝0）为绝热边界条件：

在剩下的所有其他表面上，只在平面的法向方向存在着q_c、q_r和q_e的热流损失。故

q＝－q_c－q_r－q_e（2-68）

（2）动量边界条件 熔透熔池形成以后，在熔池的上下表面，表面张力梯度和表面流体的黏性剪切力相平衡。由于贴体坐标系主要是在z轴方向与直角坐标系不同，因此，在计算空间中熔池上下表面的动量边界条件发生变化。在熔池的自由表面上，动量边界条件为

式中，γ——表面张力（N／m）；

∂γ／∂T——表面张力温度系数［N／（m·K）］。

熔池的对称面xOz两侧的物质交换为零，因此在对称面上：

在熔池的其他边界上，U、V和W均为零。

动量守恒方程式（2-49）～式（2-51）中的F_x、F_y和F_z是体积力，电弧焊熔池中的体积力包括电磁力和因温度变化而引起的浮力。

（3）初始条件 在t＝0时刻，

T＝T₀，U＝V＝W＝0（2-71）