焊接熔池的流体流动与传热的数学模型描述

按照是否与时间相关，焊接熔池流体流动和传热问题有瞬态和稳态两种。前者与时间有关，考察熔池流场和热场随时间的变化；后者与时间无关，只关心熔池流场和热场在最后稳定阶段的情况。稳态问题因为只与空间有关，相对比较简单，瞬态问题与空间和时间都相关，因此相对复杂。下面以TIG焊的瞬态热过程为研究对象，对焊接熔池内的流体流动和传热瞬态过程进行数值分析。

图2-19是运动电弧作用下TIG焊焊接过程的示意图。为了描述瞬态熔池的动态行为，需要对不同时刻焊接熔池中的传热和流体流动过程进行数值模拟。焊接过程开始后，电弧将热量传至工件，工件温度迅速升高，局部熔化形成熔池。在电弧热输入的作用下，熔池迅速长大。熔池的上表面在各种力的作用下产生变形；当工件熔透后，熔池的下表面发生下塌变形。熔池内的液体金属在多种力的作用下产生剧烈的流动，传热以对流为主；在熔池外部的固体区域，传热以热传导方式为主。随着电弧的运动，电弧下方工件上的温度分布趋于恒定，熔池形状相对于钨极稳定并不再长大，在宏观上达到准稳态，并以与电弧相同的运动速度沿焊接方向移动。这是一个三维瞬态的流体流动和传热问题。

图2-19 直角坐标系下的TIG焊焊接过程示意图

为了简化计算，在三维瞬态模型的建立过程中做出以下假设：

1）熔池中的液态金属为粘性不可压缩流体，其流动为层流。

2）只在动量方程的重力项中考虑密度的变化，遵循Boussinesq假设。

3）除了材料的比热容、热导率、粘度以及表面张力系数与温度有关以外，其他的热物理性能参数（如密度、换热系数等）均与温度无关。

尽管有文献指出熔池内流体的流动具有紊流特性，但为了计算方便起见，绝大多数研究者仍然采用层流的假设，并已证明不会引起大的误差。

在如图2-19所示的直角坐标系中，坐标系固定在工件上不动。描写焊接过程中各个物理量服从守恒原理的控制方程组包括连续性方程、能量守恒方程和动量守恒方程。它们的标准形式如下：

能量守恒方程为

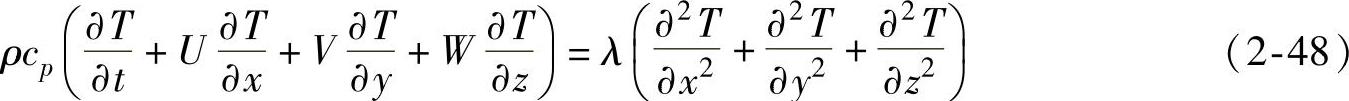
动量守恒方程为x方向：

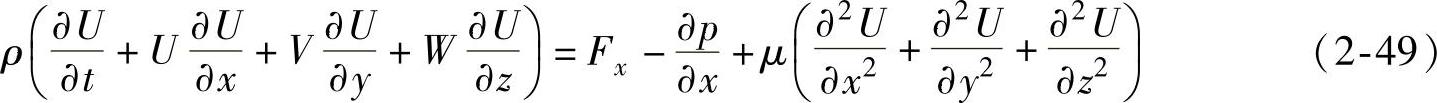
y方向：(www.xing528.com)

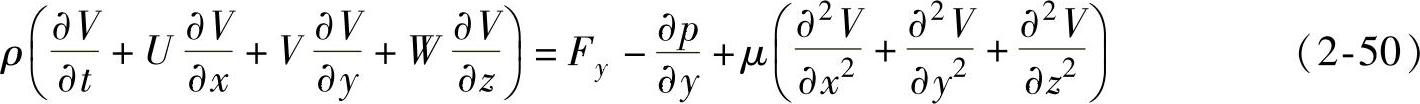
z方向：

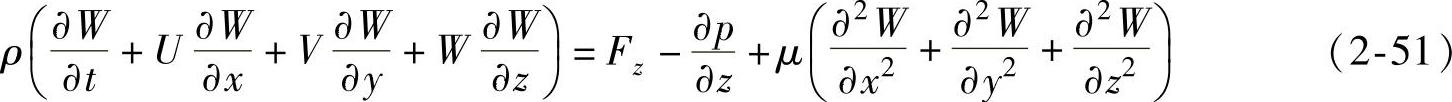
连续性方程为

式中T——温度（T），

U、V和W——流体速度在x、y、z方向上的分量（m／s）；

p——流体内的压力（Pa）；

t——时间（s）；

ρ——金属的密度（kg／m³）；

c_p——比定压热容（J／kg·K）；

λ——热导率系数［W／m·K）］；

μ——液态金属的动力粘度系数［kg／（m·s）］；F_x、F_y、Fz——体积力在x、y、z方向上的分量（N）。

在上述控制方程中，连续性方程和动量方程的求解区域是液态熔池区。由于固体区域流体速度为零，能量方程在固体区域将退化成纯粹的热传导方程。因此，能量方程的求解区域包含熔池与熔池以外的整个工件。