焊接热过程计算的解析法分析与优化

采用解析法研究焊接热过程的工作很早就开始了，H·H·雷卡林在D·罗森塞尔研究工作的基础上对焊接传热问题进行了较为系统的研究，建立了焊接热过程计算的经典理论——解析法。雷卡林首先对焊接热过程做了一些假设和简化，提出了以下观点：

1）焊接过程中材料的热物理性能参数不随温度变化。

2）被焊材料被视为固体，加热过程中无相变，不考虑焊接熔池中流体的流动。

3）焊接工件的几何尺寸无限大。按照工件几何尺寸的大小，将其分为半无限体、无限大板和无限长杆。半无限体的焊接是三维传热问题；无限大板的焊接属二维传热问题，温度只沿板平面分布，板厚度方向上无热传导；无限长杆问题被视为一维传热，在杆的横截面上热流密度为零。

4）对于厚大工件的表面堆焊，热源被视为点热源，全部集中在工件表面电弧加热斑点的中心。对于薄板对接焊，电弧被视为线热源，施加在沿板厚方向的直线微元上。而模拟焊条（焊丝）或杆件摩擦加热时，可视为面热源，即认为热源均匀地作用于杆的横截面上。

因此，雷卡林公式将全部焊接热过程的计算归纳为以下三大类问题：

1）厚大焊件焊接，采用点热源。

2）薄板焊接，采用线热源。

3）细棒焊接，采用面热源。

1.准稳态焊接温度场

正常焊接条件下，焊接热源都是以一定速度沿焊缝移动的。因此，相应的焊接温度场也是运动的。由电弧或其他集中热源产生的运动温度场，在加热开始时温度升高的范围会逐渐扩大，而达到一定的极限尺寸后，不再随时间变化，只随热源移动。即热源周围的温度分布相对于热源变为恒定，这种状态称为准稳定状态（准稳态）。当功率不变的焊接热源在焊件上做匀速运动时，所产生的相对于移动热源的焊接温度场就是准稳态温度场，其状态不随时间的变化而变化。以下主要讨论准稳态焊接温度场。

2.厚大焊件焊接时的温度场

厚大焊件连续焊接时，温度场的计算公式为

式中T₀——焊接的初始温度（K）；

q——电弧有效热功率（W）；

λ——热导率［W／（m·K）］；

v——焊接速度（m／s）；

a——热扩散率（m²／s）；

R——焊件上某点到热源中心的距离，R²＝x²＋y²＋z²（m）；x、y、z——该点在动坐标系的坐标值，热源沿x方向移动。

关于移动热源轴线上（x轴）各点的温度分布，按以下两种情况讨论：

1）在热源后方各点，R＝－x，x＜0，则由式（2-41）得

即在x轴上的热源后方各点的温度与焊接速度无关。

2）在热源前方各点，R＝＋x，x＞0，由式（2-41）得

可见，焊接速度v越大，热源前方温度的下降就越急剧，温度梯度就越大。在极大的焊接速度情况下，其热传播几乎全部在横向。

图2-8描述了x轴上的热源前后方各点的温度分布。厚大焊件上点状移动热源的温度场如图2-9所示。

3.薄板焊接时的温度场

薄板连续焊接时，温度场计算公式为

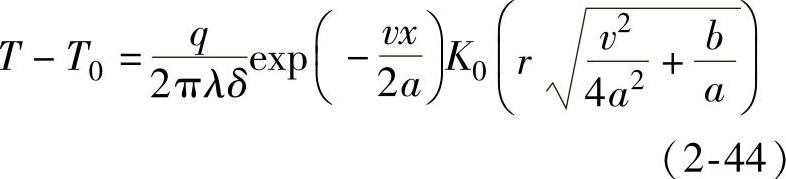
式中δ——板厚（m）；

r——焊件上某点到热源中心的距离

（m），r²＝x²＋y²；

x、y——动坐标系的坐标值，热源沿x

方向运动；

b——薄板的散热系数，b＝2α／ρc_pδ

（1／s），α为表面换热系数，

ρc_p为容积热容。

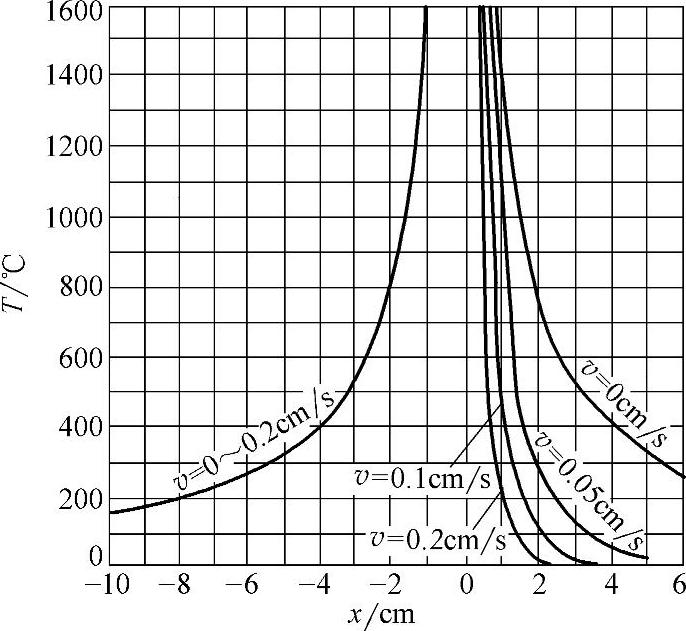
图2-8 厚大焊件x轴上热源前后各点的温度分布

［q＝4200W，λ＝0.42W／（cm·℃），α＝0.1cm²／s］

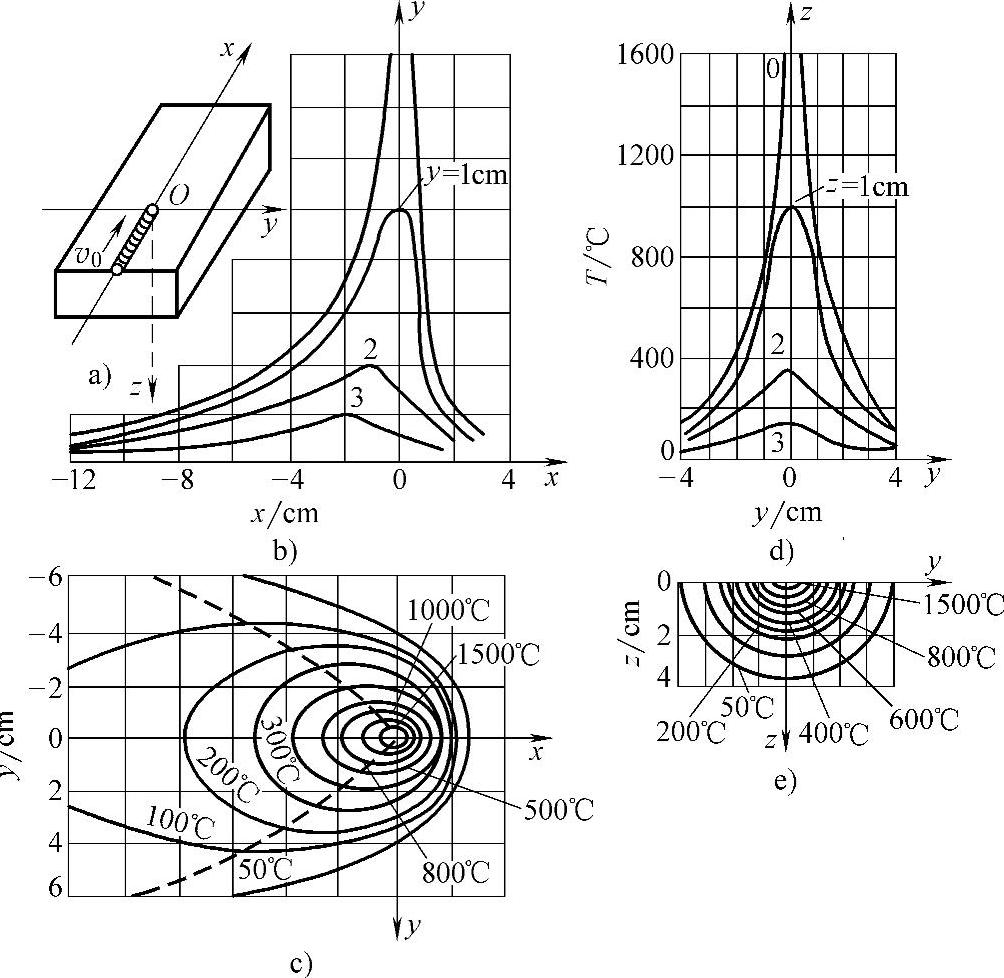
图2-9 厚大焊件上点状移动热源的温度场(www.xing528.com)

a）坐标示意图b）xOy面上沿x轴的温度分布c）xOy面上的等温线

d）yOz面上沿y轴的温度分布e）yOz面上的等温线［q＝4200W，v＝0.1cm／s，λ＝0.42W／（cm·℃），α＝0.1cm²／s］

其他参数见式（2-41）。

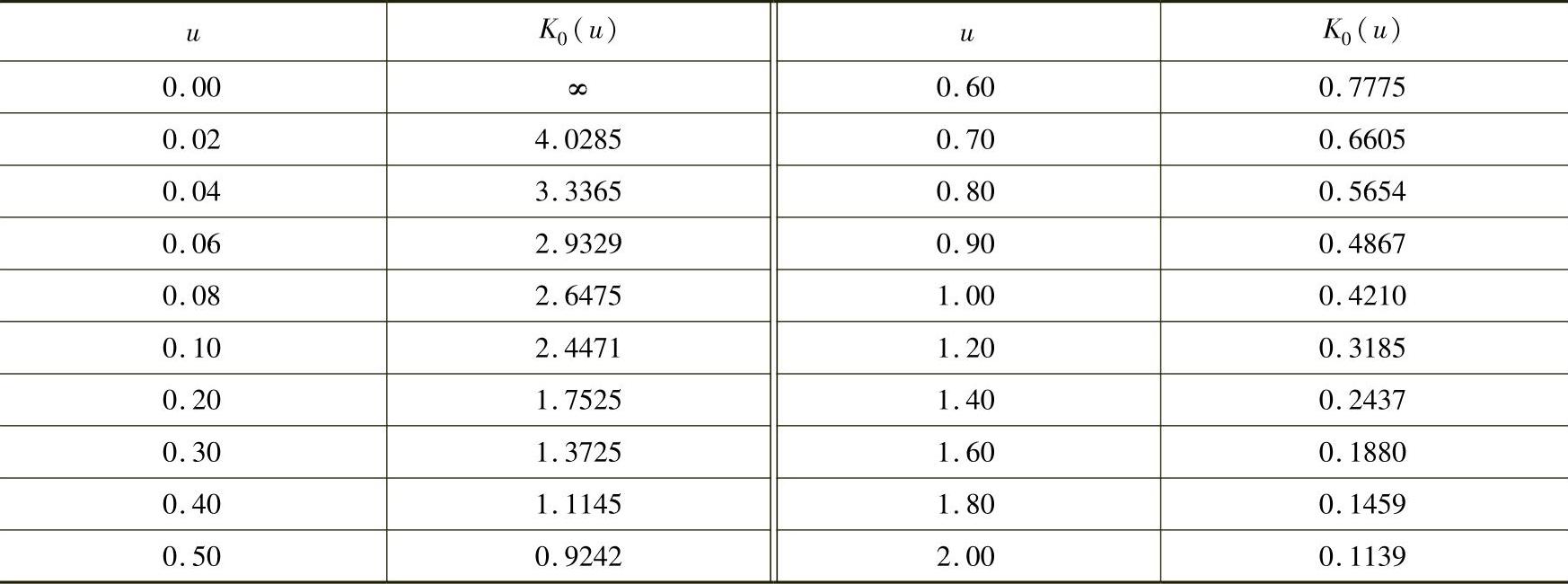
其中函数K₀是第二类虚自变量零阶贝塞尔函数，其表达式为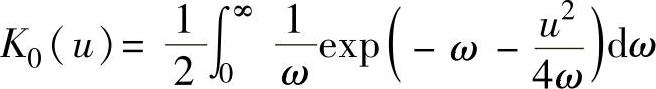，其中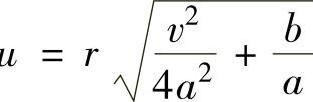，，ω是积分变量（定积分运算后ω消失）。函数K₀（u）的数值可查表。表2-5列出了一些常用范围内的K₀（u）的数值。

表2-5第二类虚自变量零阶贝塞尔函数

x轴上的温度分布并不对称于热源中心，而是在热源前方温度梯度大，后方温度梯度小，如图2-10所示。由图2-10可以看出，x轴上热源后方的温度分布与焊接速度有关，这一点与厚大焊件焊接时不同。另外，薄板焊接还考虑了表面换热的影响。图2-11所示为薄板焊接时的温度场。

4.细棒焊接时的温度场

有效热功率为q的热源，均匀作用在细棒的断面上，并以恒速v移动，达到准稳态时的温度计算公式为

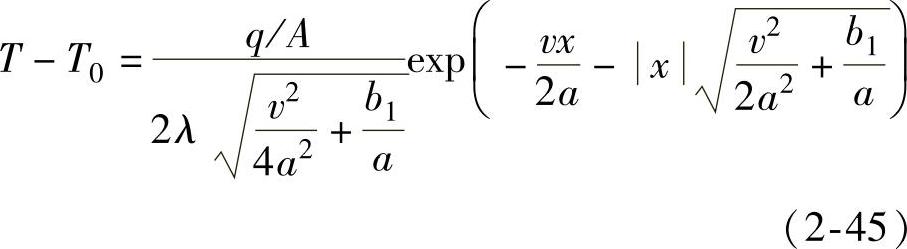
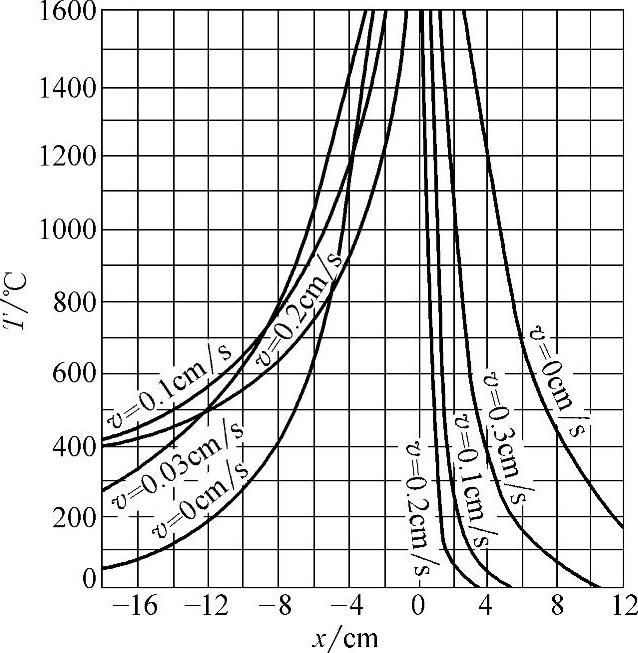
图2-10 薄板焊接时x轴上各点的温度分布

［q＝4200W，λ＝0.42W／（cm·℃），

α＝0.1cm²／s，b＝28×10^－41／s，δ＝1cm］

式中A——细棒的横截面积（m²）；

b₁——细棒表面散热系数（1／s），b₁＝αL／ρc_pA，L为细棒的周长；

x——动坐标系的坐标值，热源沿x轴运动。

其他参数见式（2-41）。

5.中厚板焊接时的温度场

以上所讨论的厚大焊件、薄板和细棒焊接时的温度场计算，都是根据半无限体、无限大板和无限长杆的假设条件而推导出来的。实际上在焊接工作中常遇到的是中厚焊件，即既不能忽略板的下表面对传热过程的影响，又不能认为温度沿板厚均匀分布。中厚焊件的传热过程，不同于厚大焊件，也不同于薄板，其传热过程有自己的特点。中厚焊件焊接时的温度场如图2-12所示。由图2-12可以看出，中厚焊件上表面传热情况与厚大焊件相似，而下表面的传热情况与薄板相似。

中厚焊件温度场的计算可以根据镜面像热源排列叠加法，也可以通过引入厚度修正系数后直接利用厚大焊件或薄板焊接时的计算公式。

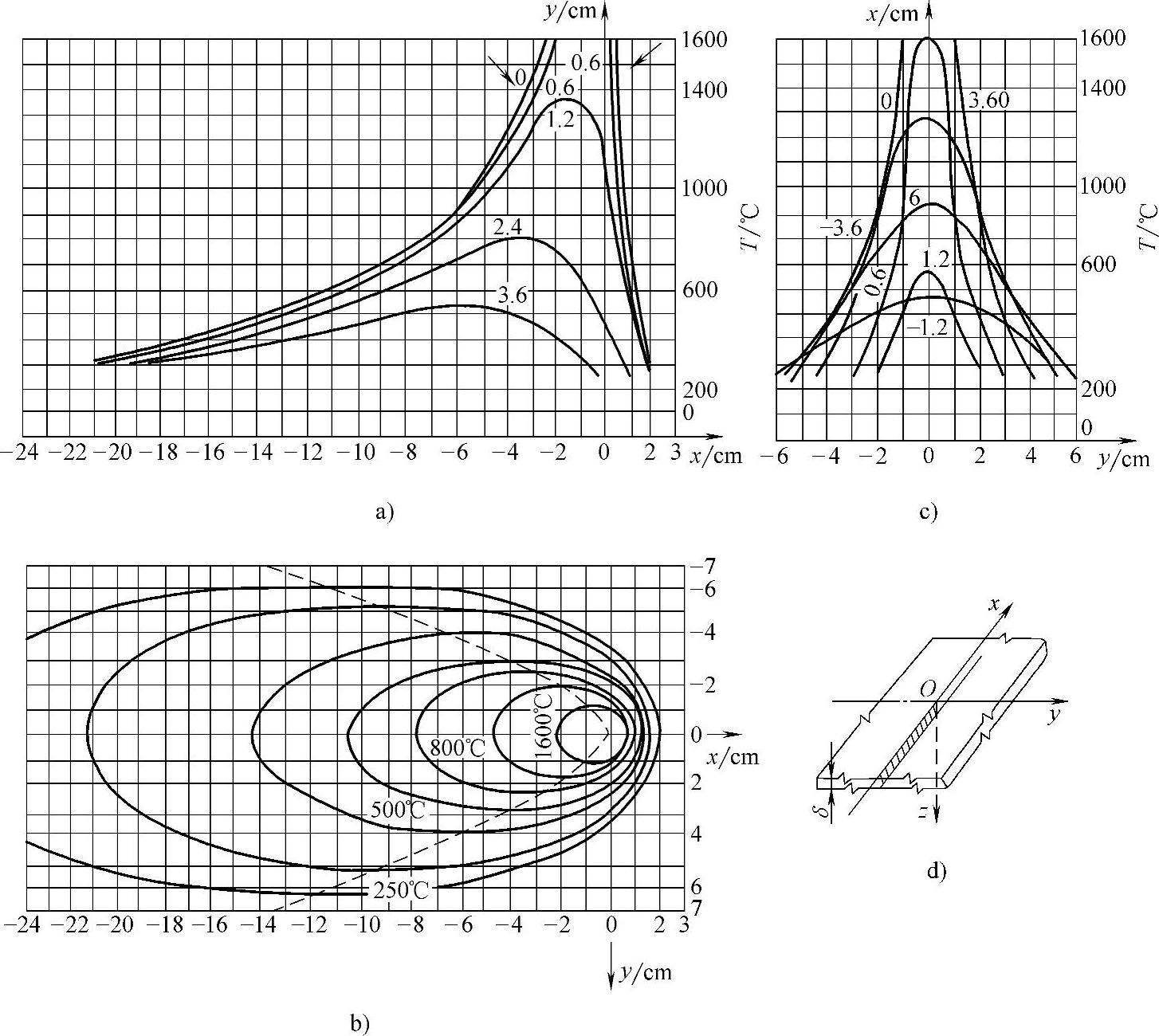
图2-11 薄板焊接时的温度场

a）xOy面上平行于x轴的温度分布b）xOy面上的等温线c）xOy面上平行于y轴的温度分布

d）坐标示意图［q＝4200W、v＝0.1cm／s、λ＝0.42W／（cm·℃）、α＝0.1cm²／s、

b＝28×10^－41／s、δ＝1cm］

6.大功率高速移动热源的温度场

在大功率高速移动热源焊接过程中，热输入功率q和焊接速度v的数值很高。定义单位长度焊缝上输入的热量q／v为热输入，其单位是J／m。若保持热输入不变，则焊接参数q和v必须成比例地增加或减少。在焊接速度v很高的时候，热传播主要在垂直于热源运动的方向上进行，沿热源运动方向上的传热很小，可忽略不计。对于厚大焊件或薄板可以将其划分为大量的垂直于热源运动方向的平面薄层，当热源通过这一薄层时，输入的热量仅在此薄层内扩散，与相邻薄层的状态无关，这种方法有助于大大提高计算速度。如图2-13所示，作用于厚大焊件高速运动大功率点热源温度的计算公式为

式中r₀——点A到热源的距离（m），r²₀＝x²₀＋y²₀；

t——热源到达点A所在截面时的传热时间（s）。

可见温度升高值正比于热输入q／v。

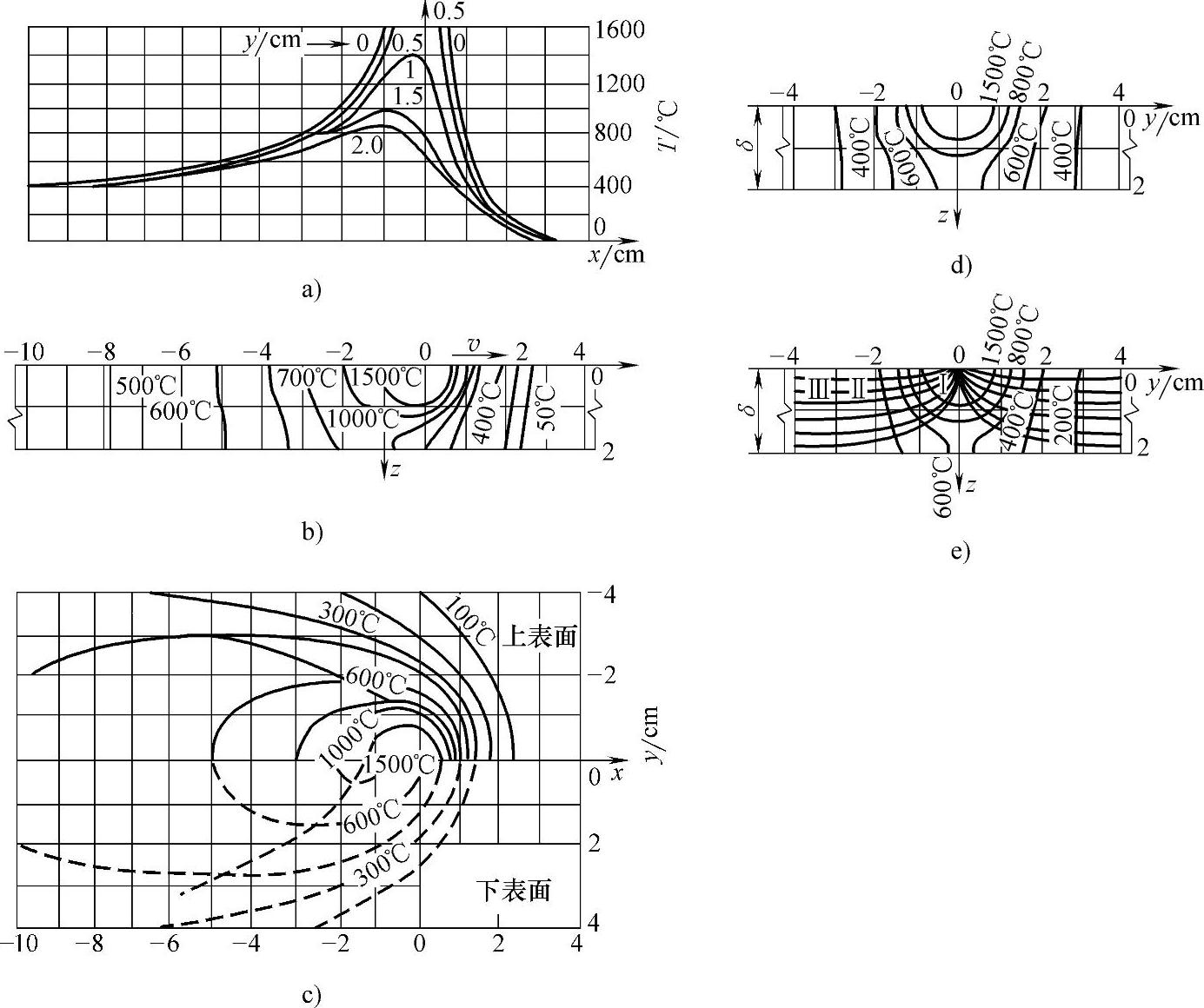
图2-12 中厚焊件焊接时的温度场

a）中厚件上表面不同y值时x方向上的温度分布曲线b）xOz平面上的等温线c）中厚焊件的上、下表面温度场d）yOz平面，x＝0时的温度分布e）yOz平面，x＝0时的热流分布（Ⅰ区相当于厚大焊件，Ⅲ区相当于薄板，Ⅱ区为无定型传热区）［q＝4200W，v＝0.1cm／s，λ＝0.42W／（cm·℃），α＝0.1cm²／s，b＝28×10^－41／s，δ＝1cm］

如图2-14所示，作用于薄板上的高速移动大功率线热源温度计算公式为

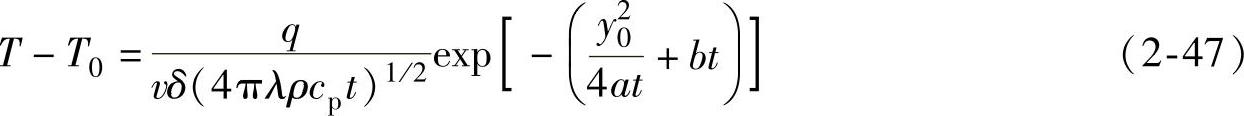
式中y₀——距热源运行轴线的垂直距离（m）。

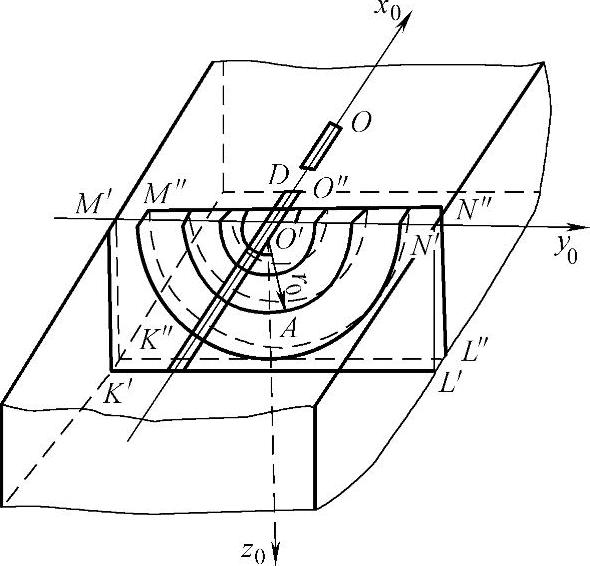
图2-13 厚大焊件上高速热源的传热模型

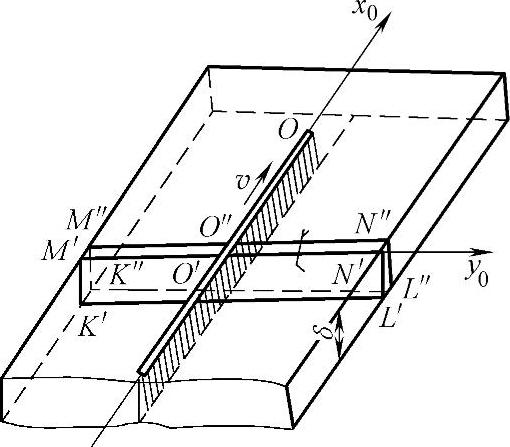
图2-14 高速热源作用在薄板上的传热模型

式（2-46）和式（2-47）也可用于一般焊接速度下的传热过程计算。焊接速度越大，计算结果就越准确。对于一般低碳钢的焊接，焊接速度大于36m／h就可应用。但应该指出的是，式（2-46）和式（2-47）只能用于热源作用点的后方毗邻焊缝的区域，而距焊缝较远的点和热源作用的前方区域均不适用。