支持向量机的原理及应用

3.3.1.1　结构风险最小化原理

针对经验风险最小化原则的缺陷，统计学习理论提出了修正结构风险最小化原则。结构风险最小化就是综合考虑经验风险和置信范围，使期望风险最小化。统计学习理论通过可变VC 维的方法达到结构风险最小化。设有函数集S=｛f（x，α），α∈Λ｝，把其分解的子函数集为

其中，每个子集的VC维满足的条件

h1≤h2≤，…，≤hk≤…

在各子集中求解经验风险最小化函数，并且在不同子集之间考虑经验风险和置信范围的影响，使期望风险达到最小，从而得出一个具有推广能力的中间子集S＊，其原理如图3-10所示。

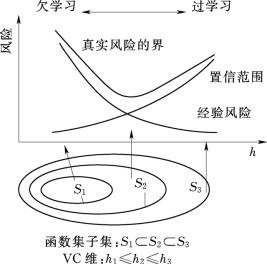
图3-10　结构风险最小化原理图

在统计学习理论中，机器学习的目的是在较小的经验风险和置信范围的情况下获得最小的期望风险，支持向量机就是在此背景下产生的新的理论方法。

3.3.1.2　最优判别超平面

与支持向量机密切相关的一个方面是最优判别超平面。假设数据如下：S=｛（x1，y1 ），…，（xl，yl）｝，xi∈Rn 称为输入空间或输入特征空间，y∈｛-1，1｝是样本的类标记，分类的目的就是寻找一个分割超平面将正负两类样本完全分开。

设｛ω·x+b=0，ω∈Rn，b∈R｝是所有能够对S 完全正确分类 （经验风险为0）的超平面的集合。完全正确分类的意义是：任意一个由法向量ω 和常数b 确定的分类超平面H＊，它对样本集S 的分类结果为

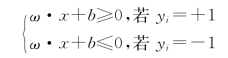
此时，观测样本（xi，yi）∈S 到超平面H ＊ 的距离为di=yi（ω·xi+b）。设d+ =min｛di｜yi=+1｝和d-=min｛di｜yi=-1｝分别为S 中的正负类样本距离H＊ 的最小距离，并由此确定两个与H＊ 平行的超平面H1 和H2 的位置，方程分别为H1：ω·x+b=d+ 和H2：ω·x+b=-d-。分析可知，H1 和H2 分别与正负两类样本相切，它们之间的区域不会出现S 中的观测样本。并且，位于H1 和H2 正中间，与它们平行的超平面H：ω·x+b=（d+-d-）／2能够等距离地分开两类观测样本，因而具有比H＊ 更优的分类性质，如图3-11所示。

将ω 和b 进行归一化，即：= 得到超平面H、H1 和H2 的归一化形式为

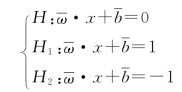
把超平面H1 和H2 之间的距离称为H 的 “分类间隔Δ”，并将H1和H2 称为H 的“间隔超平面” 或者“间隔边界”。容易计算，Δ=2／=d++d-。

所谓的 “最大间隔分类超平面” 就是在正确分类所有学习样本 ［即满足约束条件）≥1］的前提下，使得分类间隔Δ 取最大值的超平面，例如图3-11中的H。

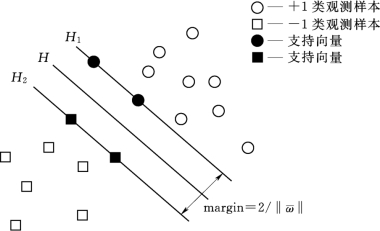
图3-11　最优判别超平面

3.3.1.3　线性样本分类

为了求解线性可分问题的最大间隔超平面，需要在满足约束）≥1的前提下最大化间隔Δ，等价于

这是一个典型的线性约束的凸二次规划问题，它唯一确定了最大间隔分类超平面。它的Lagrange函数为

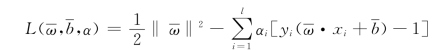
其中，αi≥0是每个样本对应的Lagrange乘子。将函数，b求其极小值，由极值条件）=0和）=0得到

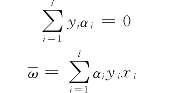
将以上两式带入Lagrange函数并考虑Wolfe对偶性质，得到优化问题的对偶问题为

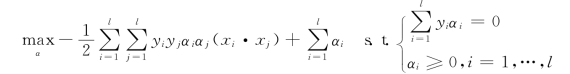
可见，对偶问题仍然是线性约束的凸二次优化，存在唯一的最优解α＊。

根据约束优化问题的Karush-Kuhn-Tucker （KKT）条件，优化上式取最优解α＊ 时应满足的条件为(www.xing528.com)

从图3-11中可以看出，由于只有少部分观测样本xi 满足）=1，它们对应的Lagrange乘子α＊ ＞0，而剩余的样本满足α＊ ＜0。我们称解α＊ 的这种性质为 “稀疏性”。

把α＊ ＞0的观测样本称为 “支持向量”，它们位于间隔边界H1 或H2 上。结合以上推导过程可知， 均由支持向量决定。因此，最大间隔超平面=0完全由支持向量决定，而与剩余的观测样本无关。这时可以得到如下的最优决策函数或者分类器

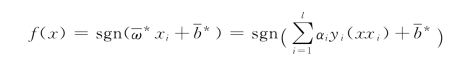
3.3.1.4　非线性样本分类

线性情况下的支持向量机，可以通过寻找一个线性的超平面来达到对数据进行分类的目的。不过，由于是线性方法，所以对非线性的数据就没有办法处理了。例如图3-12的两类数据，分别分布为两个圆圈的形状，不论是任何高级的分类器，只要它是线性的，就没法处理，因为这样的数据本身就是线性不可分的。

由于两类数据实质上是用两个半径不同的圆圈加上少量的噪声得到的，所以，一个理想的分界应该是一个 “圆圈” 而不是一条线（超平面）。如果用x1 和x2 来表示这个二维平面的两个坐标的话，其表述形式为

如果要构造另外一个五维的空间，其中五个坐标的值分别为z1=x1，z2=，z3=x2，z4=z5=x1x2，那么显然，上面的方程在新的坐标系下可写成

图3-12　线性不可分数据

新的坐标Z 是一个超平面的方程，也就是说，如果做一个映射φ：R2→R5，将X 按照上面的规则映射为Z，那么在新的空间中原来的数据将变成线性可分的，从而可使用之前推导的线性分类算法进行处理。这正是支持向量机处理非线性问题的基本思想。

以上算法也存在以下问题：①对一个二维空间做映射，选择的新空间是原始空间的所有一阶和二阶的组合，得到了五个维度；②如果原始空间是三维，会得到十九维的新空间，这个数目呈爆炸性增长，给空间映射的计算带来非常大的困难，而且遇到无穷维的情况，根本无从计算。支持向量机使用核函数解决以上问题。常用的核函数如下：

（1）多项式核

K（x，x′）=［（x·x′）+c］d

核函数为多项式的阶数d，且通常有c=0或c=1。当d=1和c=0时，实际得到的是线性核函数K（x，x′）=x·x′。

（2）径向基核

K（x，x′）=exp（-‖x·x′‖2／2σ2）

对于常见的模式识别问题，径向基核都具有优异的泛化性能。

（3）傅里叶核

一维傅里叶核为

其中核参数0＜q＜1。

总结一下：对于非线性的情况，支持向量机的处理方法是选择一个核函数，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。由于核函数的特点，使非线性扩展在计算量上增加较少，极为难得。

3.3.1.5　支持向量机的优点

相比于神经网络等传统的学习方法，采用结构风险最小化原则的支持向量机具有许多优异的性质，概括地说，它的优点主要如下：

（1）作为一种通用的学习机器，支持向量机是统计学习理论用于解决实际问题的具体实现。它在本质上是求解一个凸二次规划，从理论上说，能够获得全局最优解，从而有效地克服了神经网络等方法无法避免的局部极值问题。

（2）专门针对有限样本情况下的学习问题，采用结构风险最小化原则同时对经验风险和学习机的复杂度进行控制，有效地避免过学习现象的产生，能够获得比传统学习方法更优良的泛化能力。

（3）核函数的引入，可以将实际问题通过非线性映射到高维空间，并构造线性学习机器来实现原问题的求解。特殊性质的核函数能保证学习机器具有更好的泛化能力。同时，利用核函数巧妙地避免了高维的内积运算，使得算法的复杂度与样本维数无关，有效地避免了“维数灾难”。