静电喷涂中电压与气压的关系

粉末自喷枪口飞出后，主要受到气流推力、静电引力、重力和集尘气流的作用。这里不考虑后面两个因素的影响，主要研究气流推力与静电引力对粉末吸附到工件表面的影响。

1.粉末的动能

先推算喷枪气流推力与粉末速度和动能之间的关系。假设整个喷涂工艺处于理想状态，如图3-61所示。

1）粉末进入吸粉管时v₀=0，粉末于喷枪出口处的速度为v。

2）粉末在吸粉管和喷枪中运动的距离是S₁，并假设各处截面相同，且粉末不受阻力。

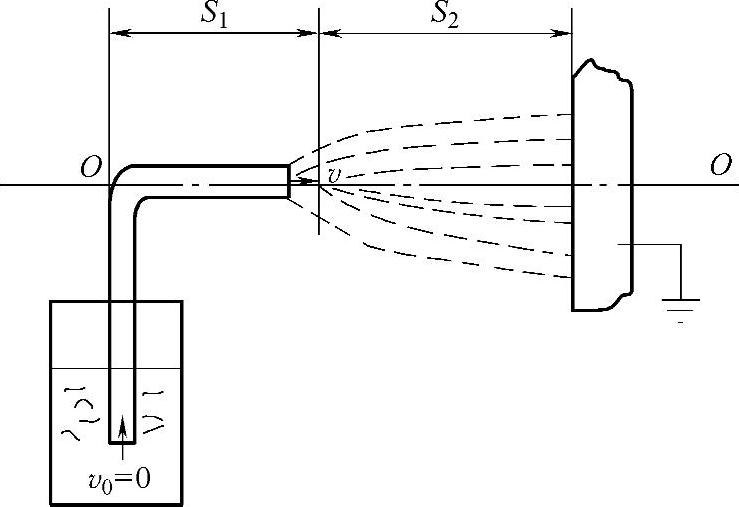
图3-61 粉末静电喷涂

3）粉末从喷枪口运动到工件表面这段距离为S₂，粉末在这段距离中会产生扩散效应。这里先研究沿O—O中心线运动的粉末流，即暂不考虑扩散效应。

4）不考虑重力和集尘气流的影响。

①计算当气流推力F₂=nF₁时，喷枪出口处粉流速度的变化V₂/V₁。

S₁=a₁t²₁=a₂t²₂

由于a₂=na₁

则由上式可得t₂=t₁/n

由于v₁=a₁t₁，v₂=a₁t₁n

喷枪口速度化为v₂=v₁n式中，F为粉末气流推力；t为粉末运行时间；S₁为粉末在粉管中运行距离；a为加速度、v为粉末到达粉枪口的速度；n为倍数。

②求粉末颗粒速度变化后的动能变化u₂/u₁。

u₂/u₁=v²₂/v²₁=n式中，u为粉末到达喷枪出口时具有的动能。

上面的关系式表明，当气流推力增大n倍时（F₂=nF₁），粉末颗粒到达枪口时的动能也增大n倍。

2.粉末流速与扩散效应的关系

现在考虑粉末离开枪口后产生的扩散效应对粉末动能的影响，如图3-60所示，由于气流推力部分消耗于扩散效应，所以沿O—O轴向的推力F₁′=K₁F₁，F₂′=K₂F₂=nK₂F₁（K₁和K₂都是小于1的常数）。(www.xing528.com)

因此扩散状态下粉末向工件运动的加速度a′=Ka。

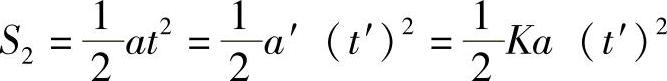
所示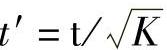

由以上各公式可求得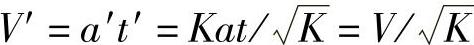

即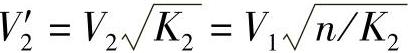

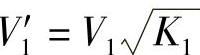
则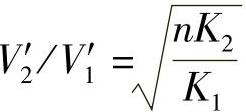

扩散效应导致粉末动能变化关系式如下：

u₂/u₁=nK₂/K₁

已知伯努利方程式：p+ρu₂+ρgh=常数，该方程式适用于粉末静电喷涂中粉末气流的运动状态，式中，p为压强，u为流速，ρ为质量密度，h为流体水平高度，排除Δ（ρgh）的变化因素，则可知当粉体流速增大时，粉流所受扩散静压推力将减少，即其在空间中的扩散效应将减弱。因此，可以说粉末气流速度变大时其K值也将变化，K₂将接近K₁值，即当v₂>v₁时，K₂将接近K₁，K₂/K₁≈1。由此可知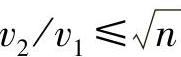：，u2/u₁≤n。

上面分析说明粉末在到达工件表面时具有的动能与其所用的喷涂气压近似呈正比关系。因此，在喷涂工艺中采用较高的喷涂气压就要求工件对带电粉末有更大的静电吸附力。静电场使带电粉末获得的电势能必须大于其动能，才能使粉末受到束缚而被吸附到工件表面上。在实际施工中粉末最终能否被吸附到工件表面还受到粉末粒径大小、集尘抽风力大小和流向、工件形状和表面状态等因素的影响。

3.粉末的电位能

现在要弄清楚粉末在静电场中怎样增加其带电量和获得更大的静电势能。根据”电晕放电”原理，如果电压低于电晕电压值时，空气中将不能产生“电子雪崩”效应，形成空间游离电子区域。粉末通过该空间时不可能获得自由电荷，也将失去静电吸附的特性。因此，电压越高粉末带电性越强。但是有人曾做过这样的实验，在工频整流电压为800V时，接地工件上虽然吸附的粉末很少，但粉末仍表现出微弱的静电吸附特性。这种矛盾现象还表现在绝缘材料也能较好地静电吸附粉末；电晕放电理论核心论点之一的自限效应实际上不存在；接地的辅助上电极对粉末静电吸附的影响比电晕电极要大得多。对于实践中出现的矛盾现象，用离子型静电吸附观点很难解释清楚。依照高分子粉末在静电场中发生电偶极化物理效应的静电吸附观点，当前静电涂装用的环氧、聚酯粉末都是带有极性基团的高分子电介质材料。这些高分子的极性基团在静电场中吸收能量后，会产生弹性联系的电偶极化行为。分子结构中的空间电荷位置发生变化，形成正负两个电荷中心。这种电荷是一种不同于自由电荷的束缚电荷，但它们一样表现出静电吸引的特征。根据理论分析可知，这种极化程度（用分子极化率α表示）同电晕电压无直接关系，而与静电场强度E值密切相关。

从图3-62的α-E曲线得知当E=100kV/cm时，α值达到饱和值。根据喷涂经验得知，当E=3kV/cm时，工件吸附粉末情况已经良好。因此在静电喷涂施工过程中运用这种理念可以认为粉末的带电量同电场强度E呈正比关系，即粉末的带电量Q=RE（R为常数）。可以求电荷在静电场中任一点a的电位能。设a与b为很接近的两点，相距ΔL，故在ab段上的场强E可看做恒量（b点为接地工件表面任一点），因为工件接地W_b=0，则W_a-W_b=EΔLQ，如图3-63所示。式中，Q为粉粒荷电量，E为电场强度，W为电位能。只有当W_a≥U_a时，a点处运动的带电粉末才无法脱开工件对它的束缚。当a点的W_a1≥U_a1时，即使粉末处于极端运动也将被电场能束缚住。当U_a2=nU_a1时，也要求达到上述状态，则E₂/E₁应是多少呢？计算如下：

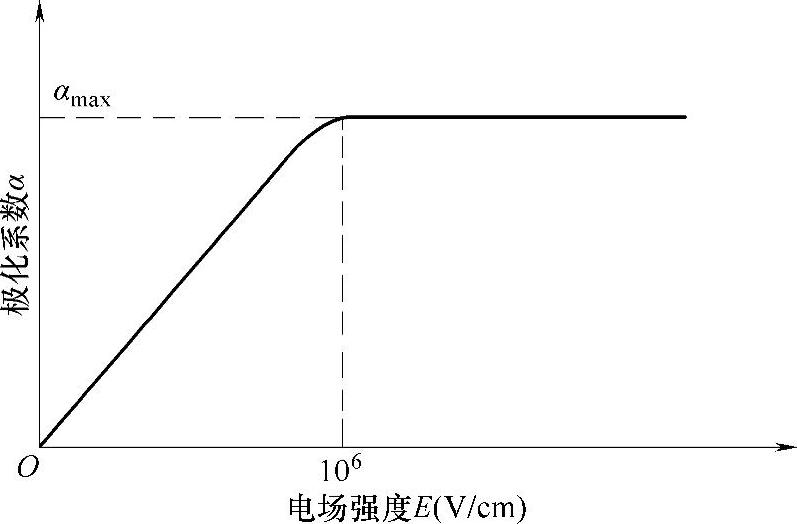
图3-62O α-E曲线图

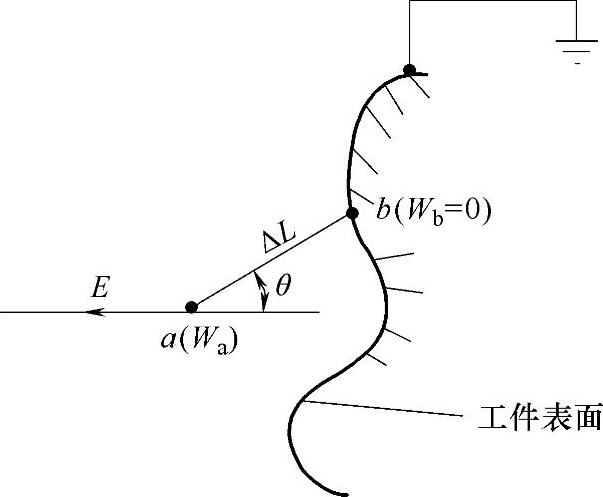
图3-63 粉末在a点的电位能

U_a1=W_a1=RE²₁ΔLOU_a2=W_a2=RE²₂ΔL则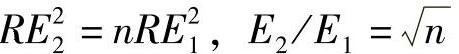（倍）