证明引理5-2的附录优化

引理5-2　如图5-1（b）所示，假设Nh和Nd可以根据系统设计需要而变化，并且满足约束Nh＋Nd＝Nsum，那么，图5-1（b）所示通信系统最大可达安全自由度为

其中，。

（1）当Nsum≤Nep－Ns时，对于任意天线对（Nh，Hd），可达安全自由度均为0；

（2）当Nsum≤Ns－Nep时，最大可达自由安全度在Nh＝0，Nd＝Nsum时取得；

（3）当Nsum＞｜Ns－Nep｜时，最大可达自由安全度在Nh＝，Nd＝Nsum－时取得，其中，

证明：可以验证，当Nsum≤Ns－Nep时，最大可达安全自由度等于Nsum，这与式（H-1）中的结果一致；当Nsum≤Nep－Ns时，最大可达自由度等于0，这同样与式（H-1）中的结果一致。因此，在下文中，我们只需要讨论在Nsum＞｜Ns－Nep｜时，最大可达自由度是否与式（H-1）中的结果一致，此时

根据文献[98]中的式（36），四节点抗窃听信道最大可达自由度为

其中，

接下来，我们就分两种情况进行讨论，即Ns≤Nep及Ns＞Nep。针对每个子情况，我们构造出Nh的一个特殊值，记作，且满足g（）＝ds，p。其后我们证明对于Nh≠，不等式g（Nh）≤ds，p总是成立。通过这样的构造办法可知函数g（Nh）在Nh＝时取得最大值。

A.当Ns≤Nep时

此时根据定义，有成立。

令，同时，令

其中，i≜Nsum－，i∈{0，1，2}。

A1.当δ≥Ns时

此时，Nsum≥Ns成立，同时，式（H-1）可以作如下简化，

另一方面，由于≥Nep，式（H-4）可以作如下简化，

将式（H-8）代入式（H-3），且联立min{，Ns}＝Ns，可知g（）＝Ns。另一方面，由式（H-3）可知，不等式g（Nh）≤Ns总是成立。因此，g（Nh）关于Nh的最大值为，

其中，由式（H-7）知（a）成立。

A2.当δ＜Ns时

此时，Nsum＜Ns成立，同时，式（H-1）可以作如下简化：

另一方面，由于，式（H-4）和式（H-5）简化为。将两者代入式（H-3），且联立，可知，

其中，由式（H-9）知式（a）成立。

接下来，我们证明对任意。由此，证明了g（Nh）关于Nh的最大值就是。为此，记

通过类似式（H-7）到式（H-10）的推导，可以验证。接下来，我们将证明对任意，都有g（Nh）≤ds，p成立。

由于对于任意成立；且根据式（H-3），g（Nh）≤Nd成立。因此，g（Nh）＜＝ds，p。在接下来的讨论中，我们只需考虑Nh≤的情况。记Nh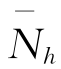＝－k，k≥1，那么，等式Nh＝＋i＋（Nep－Ns）－k，Nd＝＋k成立。此时，Nh－Nd＝＋（Nep－Ns）＋i－2k＜Nep，联立式（H-4）可知，

（1）当时，式（H-11）作以下简化，dc＝1（Nh）＝。联立式（H-5）可知，。因此，

其中，由于i≤2及k≥1，成立，因此，（a）成立；由式（H-9）知（b）成立。

（2）当时，由式（H-11）可知，dc＝1（Nh）＝0。此外，根据式（H-5）可知，，联立可知，（Nh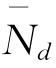）≤成立。因此，

（3）当时，由式（H-11）可知dc＝1（Nh）＝0。因此，

综合以上A1和A2两种情况可知，当Ns≤Nep时，g（Nh）的最大值为g。(https://www.xing528.com)

B.当Ns＞Nep时

此时，。

令，

其中，j≜Nsum－。根据定义，j∈{0，1，2}。此外，由于，以下等式成立，

B1.当时

此时，Ns≤δ，同时，式（H-1）可以作如下简化：

另一方面，由于≥Nep，

将式（H-13）和式（H-15）代入式（H-2）可知，g（）＝Ns。此外，根据式（H-2）可知，g（Nh）≤Ns总是成立。因此，g（Nh）关于Nh的最大值为：

其中，由式（H-14）知（a）成立。

B2.当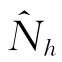＜Nep时

此时，δ≤Ns及δ≤Nsum成立，同时，式（H-1）可以作如下简化：

另一方面，＜Nep，联立式（H-5）可知，

将式（H-13）和式（H-17）代入（H-3）得到：

其中，由于式（H-16），式（a）成立。

接下来，我们证明对任意Nh≠，g（Nh）≤ds，p。由此，证明了g（Nh）关于Nh的最大值就是g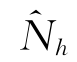（）＝ds，p。

当Nh＜，dc＝1（Nh）＝Ns－Nep及成立。因此，可以得到g（Nh）≤dc＝1（Nh）＋（Nh）≤ds，p成立。

当Nh＞及Nh≤Nd时，dc＝1（Nh）＝Ns－Nep，且

因此，可以得到g（Nh）≤dc＝1（Nh）＋（Nh）≤ds，p成立。

在接下来的讨论中，我们只需考虑Nh＞及Nh＞Nd的情况。值得注意的是，由于Nsum＝Nh＋Nd＞2Nd，当Nsum≤2（Ns－Nep）时，Nd＜（Ns－Nep）成立，联立g（Nh）≤Nd可知，g（Nh）＜Ns－Nep＜ds，p。因此，只需考虑Nsum＞2（Ns－Nep）的情况。

记，

其中，。根据定义，τ∈{0，1，2}。

将式（H-18）代入式（H-4），得到，

由联立式（H-3）可知，

对比式（H-16）和式（H-19）可知，

（1）对于任意Nh＜，记Nh＝－k，k≥1。由于Nd＝＋k，Nh－Nd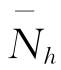＝－－2k＜Nep成立，联立式（H-4）可知，

其中，由于式（H-19），（a）成立。此外，根据式（H-5）可知，

又，由于成立，因此，

（2）对于任意Nh＞，以下不等式成立，

联立式（H-21）和式（H-22）可知，对于任意及Nh＞Nd的情况，g（Nh）≤g（）成立。联立式（H-20）可知，g（Nh）≤ds，p。