引理3-3的证明附录

引理3-3　定义自由度对域

那么，。

证明：根据定义，，因此，成立。接下来，我们将证明给定任意矩阵对（V，W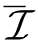）∈，总能找到这样的矩阵对，（V*，W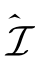）∈，使以下等式成立：ds1（V*，W）＝d1s（V*，W）＝d2s（V，W）。因此，成立。综上所述，成立。

给定任意矩阵对，W∈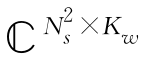。根据定义可知，（V，W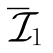）∈且（V，W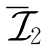）∈。由于所有矩阵都是满秩的，rank{G2W＝min{Kw，Ne}成立。在接下来的讨论中，我们分两种情况：Kw≥Ne和Kw＜Ne。

A.当Kw≥Ne时

此时，rank{G2W}＝Ne成立。作SVD分解

那么，矩阵G2WT1是不可逆的。令B＝T1（G2WT1）－1G1V，那么以下等式成立：

B.当Kw＜Ne时(www.xing528.com)

此时，G2W是满秩矩阵。令P为G2W的投影矩阵，即

由于（V，W）∈，G1V＝PG1V成立，联立式（4-2）可知，

其中，B＝（（G1W）HG2W）－1（G2W）HG1V。

综合以上两种情况，令V*＝V，W*＝W[BB⊥]，那么，对于两种情况以下等式均成立，

G1V*＝G2W（：，1：Kv）

联立（V，W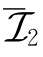）∈可知，（V*，W）∈。

另一方面，由于分开矩阵[BB⊥]是不可逆的，d1s（V*，W）＝d1s（V，W）和d2s（V*，W）＝d2s（V，W）总是成立的。