引理3-2证明附录C优化

引理3-2　定义自由度对域

那么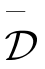，与D有相同的外边界。

证明：根据定义，⊂I，因此，D成立。接下来，我们将证明给定任意矩阵对（V，W）∈I，总能找到这样的矩阵对（V1，W），使以下不等式成立，d1s（V，W）≤d1s（V′，W），d2s（V，W）≤d2s（V′，W）。因此，D的外边界包含在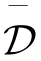的外边界之内。综上所述，与D有相同的外边界。

在接下来的分析中，基于矩阵对（（H12W）H，（H11V）H）的GSVD分解，我们将首先构造这样的预编码矩阵，去除子空间span（H12W）∩span（H11V）的同时，可达SDoF对的值不减。进一步的，基于矩阵对（（G2W）H，（G1）H）的GSVD分解，我们构造这样的预编码矩阵V′，去除子空间span（G1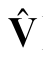）、span（G2W）的同时，可达SDoF对的值不减。通过上述办法，我们提供了预编码矩阵V′的构造方法。

首先，令A＝H12W，B＝H11V，并对矩阵对（AH，BH）作GSVD分解，记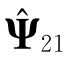对应GSVD分解得到的Ψ21，那么，

其中，由于m（V，W）≥m（，W）成立，因此不等式（b）成立。此外，令(www.xing528.com)

则span（H11∩span（H12W）＝0成立。

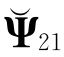接下来，令A＝G2W，B＝G1，并对矩阵对（AH，BH）作GSVD分解，记、及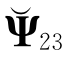分别对应GSVD分解得到Ψ21、Ψ22及Ψ23，那么，

其中，；（C-2）中不等式（b）成立，是由于

令V′＝，则span（G1V′）⊂span（G2W），且span（H11V′）∩span（H12W）＝0成立。因此，（V′W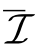）∈，并且，ds1（V′，W）＝rank{H11V′}成立。另一方面，联立式（C-1）和（C-2）可知，ds1（V，W）≤rank{H11V′}。因此，ds1（V，W）≤ds1（V′，W）。此外，由于span（H21V′）⊂span（H21V），d2s（V，W）≤d2s（V′，W）成立。