可行预编码矢量对的候选数目探究

分别定义子集合Sub11，…，Sub14，Sub21，…，Sub24中的候选预编码数目为d11，…，d14，d21，…，d24。

在上一小节中，我们通过式（4-28）、（4-32）、（4-36）及（4-40）给出了集合Sub11，…，Sub14中预编码矢量的通向式。在本章中我们假定各信道矩阵都是满秩的，因此各集合中线性无关的预编码矢量的数目满足以下不等式

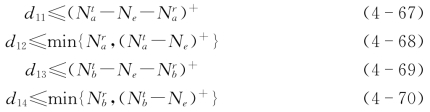
观察Sub11，…，Sub14中预编码矢量的通向式可知，不同子集合中预编码矢量扩展的子空间有时有公共部分。比如，子集合Sub21和子集合Sub11中的va具有相同的解子空间，因为其基向量Γ（Haa）Γ（GaΓ（Haa））扩展的子空间和Γ（Ga）Γ（HaaΓ（Ga））扩展的子空间相同；同理，子集合Sub21和子集合Sub13中的vb具有相同解子空间。由于我们只对线性无关的预编码矢量va和vb感兴趣，在预编码矩阵的构造过程中，从Sub21中选择出来的va和vb的数目相等。而且，以成对减小Sub11中va的候选个数及Sub13中vb的候选个数，来增加Sub21中的候选预编码矢量对，并不能增大可达安全自由度。因此，在子集合Sub21中，我们不考虑基向量Γ（Haa）Γ（GaΓ（Haa））和Γ（Hbb）Γ（GbΓ（Hbb）），这就意味着，Sub21中候选预编码矢量对的个数不超过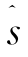，即

以上讨论同样适用于Sub22、Sub23及Sub24。因此，式（4-67）至（4-70）中的等式均取到等号。

另外一个方面，联立式（4-41）至（4-43）及式（4-49）至（4-51）可得到Sub21∪Sub22＝{（va，vb）｜Hbbvb＝0，Gava＝Gbvb≠0}。因此，

(www.xing528.com)

联立式（4-41）至（4-43）及式（4-57）至（4-59）可得到Sub21∪Sub23＝{（va，vb）｜Haava＝0，Gava＝Gbvb≠0}。因此，

联立式（4-41）至（4-43）、式（4-49）至（4-51）及式（4-57）至（4-59）可得到Sub21∪Sub22∪Sub23∪Sub24＝{（va，vb）｜Gava＝Gbvb≠0}。因此，

由式（4-23）及式（4-24）可知，四个子集合Sub2i（1≤i≤4）中，Sub21优先级最高，Sub24优先级最低。因此，式（4-71）至（4-74）不等式中的等号成立。

综上所述，在表4-1中，我们给出了各个子集合中应该考虑的候选预编码矢量对的数目。

表4-1　各子集合中候选预编码矢量对数目