可行的预编码矢量的通用表达式

（1）Sub11：此时预编码矢量应该满足以下条件：

由式（4-25）可知，va＝Γ（Ga）x，其中，x是具有合适维度大小的任非零意矢量。将va＝Γ（Ga）x代入式（4-26），得到HaaΓ（Ga）x＝0⇔x＝Γ（HaaΓ（Ga））y，其中，y是具有合适维度大小的任意非零矢量。因此，Sub11中预编码矢量的通项式

其中，z是具有合适维度大小的任意非零矢量。

（2）Sub12：此时预编码矢量应该满足以下条件：

由前面的分析可知，Gava＝0⇔va＝Γ（Ga）x。并且，由于矩阵Ga和Haa相互独立，HaaΓ（Ga）x≠0总是成立。但是，由于我们只对线性无关的预编码矢量对感兴趣，且Sub11中的预编码矢量优先级更高，所以Sub11中考虑过的预编码矢量在Sub12中不再考虑。因此，Sub12中预编码矢量的通项式为：

（3）Sub13：此时预编码矢量应该满足以下条件：

应用类似Sub11中预编码矢量通向式的推导，我们得到Sub13中预编码矢量的通项式如下：

（4）Sub14：此时预编码矢量应该满足以下条件：

应用类似Sub12中预编码矢量通向式的推导，我们得到Sub14中预编码矢量的通项式如下：

（5）Sub21：此时预编码矢量应该满足以下条件：

将va＝Γ（Haa）x和vb＝Γ（Hbb）y代入式（4-43）得到

根据第二章中的引理2-3知，满足式（4-44）中的x和y有如下通项式(www.xing528.com)

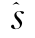其中，za和zb是具有合适维度大小的任意矢量；和由矩阵对（（GaΓ（Haa））H，（GbΓ（Hbb））H）的GSVD分解给出，且分别对应Ψ12，Λ1，Ψ22，Λ2和s。因此，Sub21中预编码矢量的通向式如下

（6）Sub22：此时预编码矢量应该满足以下条件：

将vb＝Γ（Hbb）y代入式（4-51）得到

根据第二章中的引理2-3知，满足式（4-52）中的va和y有如下通项式：

其中，和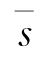由矩阵对（GaH，（GbΓ（Hbb））H）的GSVD分解给出，且分别对应Ψ12，Λ1，Ψ22，Λ2和s。由于信道矩阵Haa与Hbb、Ga、Gb均相互独立，将va代入式（4-50），不等式总是成立。因此，Sub22中预编码矢量的通向式如下：

（7）Sub23：此时预编码矢量应该满足以下条件：

应用类似Sub22中预编码矢量通向式的推导，我们得到Sub23中预编码矢量的通项式如下：

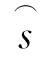其中，和由矩阵对（（GaΓ（Haa））H，GHb）的GSVD分解给出，且分别对应Ψ12，Λ1，Ψ22，Λ2和s。

（8）Sub24：此时预编码矢量应该满足以下条件：

根据第二章中的引理2-3知，满足式（4-64）中的va和vb有如下通项式

其中，和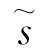由矩阵对（GHa，GHb）的GSVD分解给出，且分别对应Ψ12，Λ1，Ψ22，Λ2和s。另外，由于信道矩阵都相互独立，将式（4-65）及式（4-66）分别代入式（4-63）和式（4-62），不等式总是成立。因此，式（4-65）及式（4-66）亦是Sub24中预编码矢量的通项式。