最大可达和安全自由度达到新高度

引理4-1　给定预编码方案（Va，Vb），Alice及Bob发送信号信息的可达安全自由度可以由以下表达式给出：

其中，

证明：与引理2-2的证明过程类似，略。

根据引理4-1知，任意给定一个预编码方案，可达安全自由度等于，合法接收端无干扰子空间的维度值与窃听端无干扰子空间的维度值之差。受此启发，我们提出如下安全传输方案：来自Alice和Bob的信号对齐在窃听者Eve的同一个接收信号子空间，即所提安全传输方案中的预编码矩阵满足以下条件，

结合式（4-15）及式（4-17），可得n1（Va，Vb）＝0，n2（Va，Vb）＝0。

值得注意的是，所提安全方案与第三章中给出的安全传输方案类似，都将来自Alice和Bob的信号对齐在窃听者Eve的同一个接收信号子空间。所不同的是，在本章中，并不要求合法接收器看到的信号流数目不大于其接收天线的数目。这是由于即使某个合法接收器看到的信号流数目大于其接收天线的数目，继续增加其发送器的发送数据流数，仍有可能增加另一个合法收发器可通信的安全自由度。

引理4-2　在所提安全传输方案的约束下，可达和安全自由度不变，即，若令

则。(www.xing528.com)

证明：请查阅附录E。

根据引理4-2可知，缩小预编码矩阵的定义域，可达和安全自由度仍然不变。这样，我们在不减小可达和安全自由度的前提下，减少了需要研究的预编码矩阵的数目。接下来，我们进一步缩小预编码矩阵的定义域，通过引理4-3可知，可达和安全自由度仍然不变。

引理4-3　在所提安全传输方案的约束下，增加约束条件GaVa＝GbVb，可达和安全自由度不变，即，若令

其中，，则。

证明：请查阅附录F。

联立引理4-2和引理4-3可知，计算最大可达和安全自由度，我们只需研究集合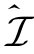。基于此，在下一小节中，我们将给出具体的预编码矩阵的设计方法。