非理想信道状态信息对方案性能的影响

在实际的通信环境中，通信节点在获取信道状态信息的时候总会引入各种误差，包括量化反馈误差、信道估计误差和时延误差等。由于预编码矩阵的设计与CSI相关联，接下来，我们给出仿真结果，展示信道估计误差对所提方案可达安全传输速率的影响。

针对信道估计误差，我们采用如下Gauss-Markov模型进行建模[96]：

其中，0≤α≤1表示信道估计误差系数，α值越大表示信道估计越不准确，α＝0对应完美信道状态信息情况，α＝1对应信道状态信息完全未知的情况；dei表示Eve到Si的距离；矩阵和Δ分布代表信道状态信息的估计值和误差值。矩阵中的随机元为ejθ，其中θ服从均匀分布，取值区间为[0，2π）。矩阵Δ中的随机元服从均值为0，方差为1的高斯分布。类似的，我们采用Gauss-Markov模型对信道Hij，i＝1，2，j＝1，2，进行建模。S1固定在坐标点（10，0），接收器处的噪声功率σ2＝－60dBm。具体的，在每次信道遍历中，我们将信道状态信息的估计值代入表3-3中，计算预编码矩阵。

图3-8给出了不同天线配置情况下，平均可达安全传输速率随信道不确定性参数α的变化曲线。具体的，N1＝Ne＝4，我们分别考虑N2＝2，N2＝3和N2＝7的情况。由图可以看出，随着信道估计误差的增加，可达安全传输速率逐步下降。值得一提的是，随着N2值的增大，可达安全传输速率下降的趋势有所缓和。另一方面，将N2＝2对应的曲线与图3-4中σ2＝－60dBm的情况对比，可以看出，α＝0.2和S1－S2之间距离10米，与α＝0和S1－S2之间距离50米，可达安全传输速率大致相等。这表明，通过拉近S1与S2之间的距离，能够减小信道估计误差对可达安全传输速率带来的影响。

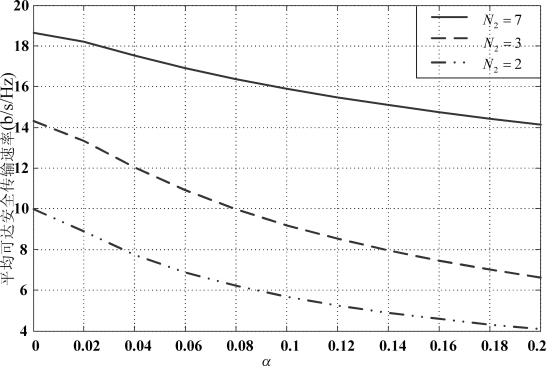
图3-8　平均可达安全速率随S2天线数及信道估计误差的变化曲线

接下来，我们分别考虑到合法接收端的信道矩阵Hij和到窃听端的信道矩阵Gi存在估计误差的情况，并给出所提传输方案可提供的安全速率随信道估计误差系数α的变化趋势。图3-9和图3-10分别考虑了N2＝2和N2＝6的情况，根据式（3-67）可知，此时分别可以实现（2，0）和（3，3）的自由度对。(www.xing528.com)

图3-9　平均可达安全速率随信道估计误差的变化曲线，Case 1

图3-10　平均可达安全速率随信道估计误差的变化曲线，Case 2

由仿真结果可以看出，当N2＝2时，可达安全传输速率随信道矩阵Gi估计误差的变大而减少，但是并不随信道矩阵Hij估计误差的变大而变化；在N2＝6时，可达安全传输速率不仅随信道矩阵Gi估计误差的变大而减少，也随信道矩阵Hij估计误差的变大而减少。针对这个现象，可以作以下解释。根据表3-3可知，所提预编码矩阵的构造不仅与信道矩阵G1和G2相关联，同时也与Γ（H12）、Γ（H21）和H22相关联。由于所提预编码矩阵计算方案只关心D1处总的信号流数目，所以信道矩阵H21和H22只会影响通信链路S1－S2可支持的传输速率。当N2＝2时，N2s≤N1d，H12并没有零空间，因此预编码矩阵的计算只与信道矩阵G1和G2相关联。相比之下，当N2＝6时，预编码矩阵的计算同时取决于信道矩阵G1、G2和Γ（H12）。

值得注意的是，当信道矩阵Hij无法获知时，通过稍微更改所提方案，我们仍然能够获得一定大小的安全自由度。具体的，由于H12和H21未知，我们无法得知这样的预编码矢量，使得信息信号不对其他用户产生干扰。即，d1＝d3＝d4＝d5＝0，d1＝（Ns1－Ne）＋，d6＝s～。将这些参数代入式（3-67）可知

基于式（3-69），可以计算出此时最大可达的自由度域。此外，将这些参数代入表3-3，能够计算出实现这些自由度对的预编码矩阵对。具体的，根据式（3-69），当N1＝Ne＝4，N2＝6时，可以实现自由度对（2，2）。我们根据表3-3计算实现自由度对（2，2）的预编码矩阵对，并计算可达安全传输速率。如图3-10，和预料的一样，S1－D1通信链路仍然可以支持可观的安全传输速率。