构造发射预编码矩阵的优化方法

由3.4.4小节的分析可得到，实现可达自由度域的预编码矩阵的构造办法。具体的，我们从集合Subo≜Sub1∪Sub3∪Sub5中入选u＝min（，min{ymax，d5}＋d1＋d3）个预编码矢量对，从Sube中入选t＝（－u）＋个预编码矢量对。这样的构造办法既能满足d1s＝，同时在D2处预留了维度为d2s＝的无干扰接收子空间。如果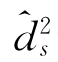≤rank{W（：，1：Kv）}，S2不需再添加其他预编码矢量，便能实现d2s＝的自由度；否则，S2通过增加－rank{W（：，1：Kv）}个满足一定条件的预编码矢量，同样能实现d2s＝的自由度。具体的，从Γ（H12）中选择个列向量，从R中选择前个列向量，使得预编码矩阵W满足Kw＝。其中，R由SVD分解H22＝USRH得到。通过SVD分解，H22被分解为平行的几个子信道，其中前个子信道的信道质量最好。表3-3总结并给出了发射预编码矩阵的构造办法。

表3-3　实现最大可达自由度域的预编码矩阵对的构造办法

例3-4：考虑场景（Ns1，N1d，Ne）＝（6，5，5），（Ns2，Nd2）＝（6，4）。根据例3-3，我们得知自由度对＝（2，4）是该场景中自由度域边界上的一个点。根据3.4.4小节的计算过程可知，在该边界点上，ymax＝2，zmin＝0，所以，u＝2。又，由于d1＝d3＝0，d5＝2，我们将首先从Sub5中选入2个矢量对，分别记作（v1，w1），（v2，w2）。由于t＝0，我们不再从子集合中入选其他矢量对。至此，矩阵V＝[v1　v2]，矩阵W（：，1：Kv）＝[w1　w2]。由于，，接下来，我们从Γ（H12）中入选一个矢量，记作w3，从R中选择对应最大奇异值的特征向量，记作w4。最后，我们得到预编码矩阵V＝[v1　v2]，W＝[w1　w2　w3　w4]。根据定义，H11v1≠0，H11v2≠0，H12w4≠0，H22wi≠0（1≤i≤4），因此，(www.xing528.com)

dim{span（H11V）}＋dim{span（H12W）}＝2＋3＝5

dim{span（H22W）}＋dim{span（H21V）}＝4＋0＝4

这表明，该矩阵对能实现自由度对＝（2，4）。