计算可达自由度域

计算可达自由度域的核心思想是，固定d1s的值，最大化d2s的值。假定预编码矩阵V由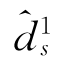列预编码矢量组成，其中z列矢量来自集合Sube≜Sub2∪Sub4∪Sub6，即S1发出的信号对D2产生干扰。那么，D2最多能看到维度为（N2d－z）＋的无干扰子空间。因此，

另一方面，由式（3-17）可知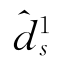，＋dim{span（H12W）}≤Nd1总是成立。因此，

联立式（3-61）、式（3-63）及（3-64）可知，

观察式（3-65）可知，为了最大化ds2的值，我们只需要最小化z。根据表3-1，在没有约束d1s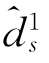＝的情况下，z的最小值等于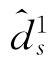（－（d5＋d1＋d3））＋。但是，由于d1s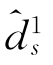＝成立，且Sub5中的预编码矢量满足H12w≠0，能从Sub5中入选的矢量对数目受到限制。例如，考虑场景d1＋d3＝2，d5＝2，N1d＝3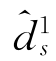，＝3。如果不考虑约束d1s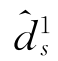＝＝3，z的最小值为0，此时至少从Sub5中入选一个预编码矢量对。但是，由于Sub5中的预编码矢量满足H12w≠0，如果从Sub5中入选一个预编码矢量对，中不等式（3-17）依然成立的前提下，我们最多还能从Sub1∪Sub2∪Sub3∪Sub4中入选一个矢量对。这样，d1s的最大取值为2，这与假设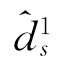＝3矛盾。

记x和y分别为从Sub1∪Sub2∪Sub3∪Sub4及Sub5∪Sub6中入选的矢量对。那么，在满足约束d1s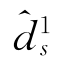＝的情况下，y的最大值可以由以下优化问题给出：

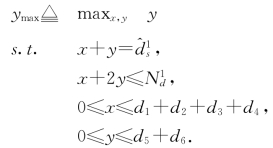(www.xing528.com)

求解以上优化问题，可得，

因此，我们至多能从Sub5中入选min{ymax，d5}个矢量对，z的最小值如下：

将式（3-66）代入式（3-65），得到ds2的最大值如下：

表3-2　可达自由度域的计算过程

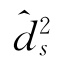例3-3：考虑场景（N1s，N1d，Ne）＝（6，5，5），（N2s，N2d）＝（6，4）。分别根据式（3-61）和（3-62）可知，＝3。首先，初始化＝3，并将其代入式（3-67），得到＝3；由于，令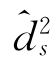＝2，并将其代入式（3-67），得到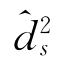＝4；由于此时，因此停止迭代。输出所有自由度对，即＝（3，3）和＝（2，4）。