最大安全自由度域的探索与优化

计算可达安全自由度域的核心思想是，在给定d1s的情况下，记，尽可能的最大化ds2。结合引理3-2和引理3-3可知，为了确定最大可达安全自由度域，我们只需要研究预编码矩阵集合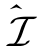。根据引理3-1可知，对于任意给定预编码矩阵对，（V，W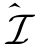）∈，可达安全自由度为ds1＝rank{H11V}。在本小节中，我们构造这样的预编码矩阵对（V，W），使得，且同时为D2预留出最大的无干扰的接收信号子空间。

记矢量对（v，w）为构成矩阵对（V，W）的列。显然的，我们只对线性无关的矢量感兴趣。关于（v，w），以下几点性质将在后续分析中相继用到：首先，当来自S1的信息信号落在窃听信道的零空间里时（即，G1v＝0），即使w≠0，来自S2的共信道干扰信号也不能进一步恶化窃听信道，因为此时窃听者已经不能窃取任何信息；第二，根据引理2-2，对于任意给定预编码矩阵对（V，W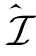）∈，可达安全自由度d1s＝rank{H11V}。因此，在满足约束（V，W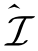）∈的条件下，入选的线性无关的矢量对数目越多，d1s越大；第三，在满足约束（V，W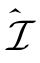）∈的条件下，最多可入选的线性无关矢量对的数目由式（3-16）决定，即，

第四，D2处无干扰的接收信号子空间的维度取决于D2是否受来自S1的信号的干扰。基于以上几点，我们将满足条件的矢量对（v，w）划分成六个子集合，即Sub1，Sub2，…，Sub6。

Sub1：来自S1的信息信号落在窃听信道的零空间里（即G1v＝0），并且没有对D2造成干扰（即H21v＝0）。此时，即使没有共信道干扰，所传输的信息数据也是安全的。因此，我们取w＝0。(www.xing528.com)

Sub2：来自S1的信息信号落在窃听信道的零空间里，但是将对D2造成干扰（即H21v≠0）。

Sub3∪Sub4∪Sub5∪Sub6：来自S1的信息信号落在窃听信道零空间的正交补空间里，即G1v≠0；同时，Sub3中的矢量对满足H21v＝0，H12w＝0，即，来自S1和S2的信号分别对D2和D1无干扰；Sub4中的矢量对满足H21v≠0，H12w＝0；Sub5中的矢量对满足H21v＝0，H12w≠0；Sub6中的矢量对满足H21v≠0，H12w≠0。

我们定义有能力支持更大自由度对（d1s，d2s）的集合，为在构造预编码矩阵中拥有更高优先级的集合。在预编码矩阵的构造中，我们将按照优先级由高至低，依次从各个子集合中入选预编码矢量对。接下来，我们将首先给出每个子集合中va和vb的通向表达式。这些通向式可能具有相同的基向量，而我们只对线性无关的矢量感兴趣，因此，低优先级集合的候选预编码矢量对将对应地减少。分别定义Sub1，Sub2，…，Sub6中候选预编码矢量对的个数为d1，d2，…，d6。基于各子集合的优先级大小，以及各子集合中va和vb的通向表达式，我们最后给出d1，d2，…，d6的表达式。