一种启发式的预编码矩阵构造方案

本小节在2.4.2小节中所提的安全传输方案中的约束下，给出一种启发式的预编码设计方案。由2.4.2小节可知，在所提安全传输方案下，可达安全自由度ds（V，W）＝rank{H1V}。因此，预编码方案设计的核心思想是：在满足约束（2-15）（2-16）的前提下，尽可能多地增加Alice发送的线性无关的数据流数目。记（v，w）为满足（2-15）（2-16）的预编码矢量对，在预编码的设计中，我们在满足约束条件的情况下，尽可能多地增加发射端预编码矢量对（v，w）的数目。为此，我们考虑以下三种情形（见图2-2）：

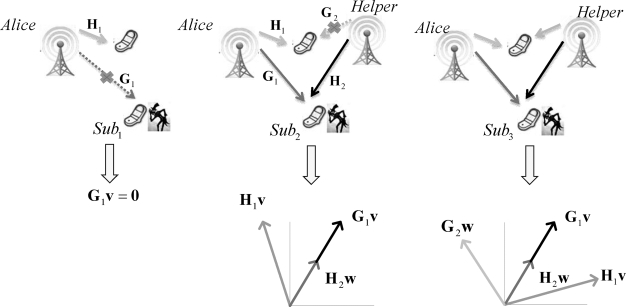
图2-2　发射端预编码矢量对的三种情况

Sub1：来自Alice的信息信号落在窃听信道的零空间里，即G1v＝0。此时，即使没有Helper的人工噪声护航，所传输的信息数据也是安全的。Sub2∪Sub3：来自Alice的信息信号落在窃听信道零空间的正交补空间里，即G1v≠0；同时，设计Helper处的人工噪声，使得G1v＝H2w。此外，Sub2中w满足G2w＝0，Sub3中w满足G2w≠0。

由于所有的信道矩阵是满秩的，式（2-16）中的约束条件可以等价写为

在预编码矩阵的构造中，定义有能力支持更多数据流的集合具有更高的优先级。那么，根据式（2-17）可知，Sub1种的预编码矢量对具有最高优先级，Sub2次之，Sub2的优先级最低。

一种启发式的预编码矩阵构造方案：定义di（i＝1，2，3）分别为Subi（i＝1，2，3）中候选预编码矢量对的个数。从物理意义的角度出发，在预编码矩阵的构造过程中，我们只考虑线性无关的预编码矢量。我们依次考虑从Sub1，Sub2，Sub3中逐个入选预编码矢量对，直到式（2-17）中的不等式不再成立或者当前子集中候选预编码矢量全被选完。

接下来，我们将决定各子集中候选预编码矢量对的个数及其通向表达式。根据定义，Sub1中的矢量对满足G1v＝0，因此其预编码矢量的通向表达式v＝Γ（G1）x，

同样，根据定义，Sub2∪Sub3中的矢量满足G1v＝H2w，为了找到满足条件的矢量对，在下文中，我们将首先给出GSVD分解及其性质。基于GSVD分解，我们将给出Sub2和Sub3中预编码矢量对的通向式，以及候选预编码矢量对的个数。

GSVD分解：任意给定两个满秩矩阵A∈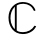N×M和B∈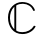N×K。根据文献[94]，矩阵对（AH，BH）的GSVD分解返回酉矩阵Ψ1∈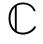M×M和Ψ2∈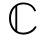K×K，非负对角矩阵D1∈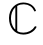M×k和D2∈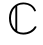K×k，以及矩阵X∈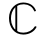N×k，rank{X}＝k，使得以下关系式成立

其中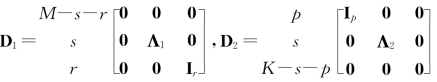，。在这里，对角矩阵Λ1∈Rs×s和Λ2∈Rs×s的对角元素均大于0，且DH1D1＋DH2D2＝I成立。此外，以下等式成立

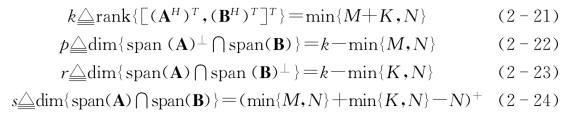
结合分块矩阵，式（2-19）和（2-20）可以分别重新写成以下形式

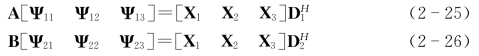(www.xing528.com)

其中，Ψ11，Ψ12和Ψ13分别对应Ψ1的前M－s－r列，第M－s－r＋1到M－r列，第M－r＋1到M列；Ψ21，Ψ22和Ψ23分别对应Ψ2的前p列，第p＋1到p＋s列，第p＋s＋1到K列；X1，X2和X3分别对应X的前p列，第p＋1到p＋s列，第p＋s＋1到p＋s＋r列。

通过GSVD分解，我们将矩阵A和B扩展成的子空间划分成立三个子空间。为了更加形象的描述，我们在图2-3中给出GSVD分解中各矩阵对应的几何意义。

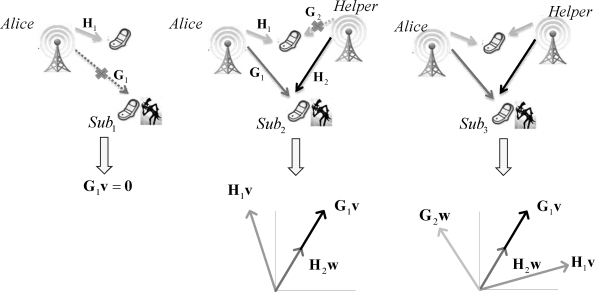
图2-3　GSVD分解

引理2-3　任意给定两个满秩矩阵A∈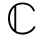N×M和B∈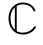N×K。根据文献[94]，矩阵对（AH，BH）的GSVD分解返回酉矩阵Ψ1∈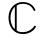M×M和Ψ2∈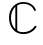K×K，非负对角矩阵D1∈M×k和D2∈K×k，以及矩阵X∈N×k，rank{X}＝k。那么，

（1）Av＝Bw≠0成立，当且仅当

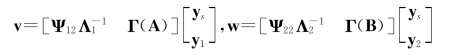
其中，Γ（A）表示矩阵A的零空间的基向量，ys表示具有合适长度的任意非0向量，y1和y2表示具有合适长度的任意向量。

（2）满足Av＝Bw≠0线性无关的v的个数为s＋dim{null（A）}。

证明：请查阅附录B。

根据定义，Sub2∪Sub3＝{（v，w）｜G1v＝H2w≠0}。对矩阵对（GH1，HH2）作GSVD分解，得到的Ψ12和Ψ22分别对应满足G1v＝H2w≠0的v和w；又，信道G2与G1、H2相互独立，因此此时G2w≠0总是成立，所得v和w就是集合Sub2中预编码矢量对的通项式。另外一方面，结合引理2-3可知，集合Sub2和Sub3中的候选预编码矢量对数目之和满足

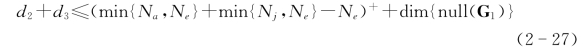
此外，根据定义，Sub2＝{（v，w）｜G1v＝H2w≠0，G2w＝0}。令w＝Γ（G2）y，将其代入G1v＝H2w≠0，得到G1v＝H2Γ（G2）y≠0。对矩阵对（G1H，（H2Γ（G2））H）作GSVD分解，得到的Ψ12和Ψ22分别对应满足G1v＝H2Γ（G2）y≠0的v和y，由此得到集合Sub2中预编码矢量对的通项式。另一方面，结合引理2-3可知，集合Sub2中的候选预编码矢量对数目满足以下关系

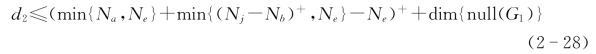
由于在预编码矩阵的构造中，Sub1具有最高优先级，Sub2次之，Sub3的优先级最低。此外，在预编码矩阵的构造中，我们只考虑线性无关的预编码矢量对，因此，Sub1中的波束成形方向将不在其他两个子集中考虑，并且我们尽可能地增加优先级高的子集中的候选预编码矢量对的个数。结合式（2-27）和（2-28），可以得到

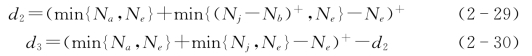
例2-1：考虑这样的一个场景，其中Na＝Nb＝3，Nj＝4，Ne＝3。由式（2-18）（2-29）（2-30）可知，d1＝0，d2＝1，d3＝2。由于在预编码矩阵的构造中，Sub1的优先级最高，Sub2次之，Sub1的优先级最低。因此，我们将首先从Sub2中选入一个预编码矢量对，记作（v1，w1）；接着，从Sub3中选入一个预编码矢量对，记作（v2，w2）。我们不再选择其他的矢量对，因为约束条件（2-17）将不再成立。所以，最后构造好的预编码矩阵V＝[v1，v2]，W＝[w1，w2]。根据Sub2的定义，G2w1＝0。结合式（2-12）可得，此时可达安全自由度为2。