纺织品检测数据处理学习任务

对纺织品具体的性能实施检测后，会获得相关检测数据，对于这些检测数据受各种因素影响会存在一定误差或者出现异常情况，需要加以控制和消除，来提高和保证检测数据的准确性。

一、误差的分类与处理

在检测中，不可能得到百分百的真实值，只能是一个与真实值相近的值，这个值与真实值之间的差异，称为测量误差，简称误差。从不同的角度出发，误差分类也不相同。

1.按误差的来源分类

按误差的来源不同可以分为人员操作误差、环境条件误差、仪器误差和抽样误差。人员操作误差主要是由于操作人员操作不规范造成的，比如测试人员在读数时的视差等。环境条件误差主要是环境变化造成的，如温湿度的变化、电磁场的影响、电源的干扰等。仪器误差主要是仪器本身的原因造成的，如所用仪器不适合、仪器未按标准校正等。抽样误差主要是面对被测的对象往往总体很大，需要采取抽样测量，但抽样时有可能抽样方法不当、所得样品不具有代表性等所造成的误差。

2.按误差产生的原因分类

按误差产生的原因不同可以分为系统误差、随机误差和过失误差。系统误差又称可测误差，是指在重复性条件下，对同一被测量对象进行无限多次测量所得结果的平均值与被测量真值之差。系统误差具有单向性、重复性的特点，影响比较固定，有规律可循，一般可以通过定期校正仪器，按照标准规范操作等途径予以修正或消除。在实际检测中，应尽量避免系统误差。随机误差也称偶然误差，是随机产生的，具有偶然性因素，难以控制。实践证明，随机误差遵循正态分布，可以依照正态分布的特性来处理。过失误差也称不正当误差、疏失误差或粗大误差，它是测量人员疏忽、疲劳或是操作出错等原因造成的，在测量中要尽可能避免。过失误差没有任何规律可循，比较明显，要按照规定的法则将其从结果当中剔除。

3.按误差的表示方法分类

按误差的表示方法不同可以分为绝对误差和相对误差。绝对误差是测定值X与真实值x之差，以ΔX=X-x来表示。但x是未知的，而X是波动的，因此ΔX可正可负。在实际检测中，只要没有明显的系统误差，在次数足够的情况下，可以用测定值的算术平均值来代表其真实值。

由于绝对误差不能用作误差大小的相对比较，此时只能用相对误差δ，相对误差是以绝对误差与真实值的比值来表示，即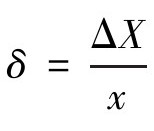。在实际应用中可以用X来近似代替x，则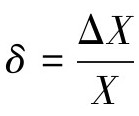。如果δ值大，说明X偏离x远，则测试的精确度就差，因此在误差运算中，有时采用相对误差比绝对误差更科学。

在系统误差、随机误差和过失误差中，随机误差难以控制，过失误差可以尽量避免，因此关键就在于系统误差的处理。系统误差又称可测误差，是由某些固定的原因造成的。一般可以采用数据分析、理论分析或对比分析的方法发现系统误差。系统误差具有单向性、重复性的特点，影响比较固定，因此可以测定校正。主要通过以下几个方面来消除和修正误差。

（1）从产生的根源上消除系统误差是最根本的方法，因此要对检测过程中有可能产生系统误差的各个环节仔细分析，如合理选用仪器设备、调整好仪器设备的状态等，最大限度地减小和消除系统误差。

（2）引入修正项消除系统误差，对各种误差因素进行充分研究，计算出误差，以与误差数值大小相同而符号相反的值作修正值引入修正。

（3）选择适合的测量方法减小和消除系统误差。

①代替法，首先对被测对象进行测量，接着用一个标准量代替，再次测量，求出两者之间的差值，从而消除误差。

②异号法，进行两次测量，使得两次测量中的误差大小相等、符号相反，从而消除系统误差。

③交换法，根据误差产生的原因，将测量过程中的某些条件交换，使产生系统误差的原因对测量结果起相反的作用，而消除系统误差。

在实际中可以选择使用其中一种或多种进行。

二、异常值的处理与修约

在实际的检测中，获得测试数据后，会遇到个别数据比其他数据明显偏大或偏小，这样的数据被称为异常值。异常值的出现有两种情况，一种是被测总体固有的随机变异性的极端表现，属于总体的一部分；另一种是由于测试条件和方法的偏离或是观测、计算、记录的失误造成的，不属于总体。

对于异常值的处理，可以按照GB/T 4883-2008《数据的统计处理和解释正态样本离群值的判断和处理》、GB/T 6379.1～6测量方法与结果的准确度系列标准进行。

在对检测数据结果进行处理过程中通常还需要按照相应的标准进行修约。修约的过程应遵循GB/T 8170-2008《数值修约规则与极限数值的表示和判定》中的规定。在此对规则做简要的介绍。(www.xing528.com)

1.小于5

拟舍弃数字的最左一位数字小于5时，则舍去，即保留的各位数字不变。

范例：将22.1498修约到一位小数，其拟舍弃数字包括“498”，最左一位数字为“4”，因此舍弃得22.1。同理如果要将22.1498修约成两位有效位数，得22。

2.大于或等于5

拟舍弃数字的最左一位数字大于5，或者虽然等于5，但其后跟有并非全部为0的数字时，则进一，即保留的末位数字加1。

范例：将2268修约到百位，得23×102（特定时可以写为2300）。将2268修约成三位有效位数，得227×10（特定时可以写为2270）。将20.502修约到个位，得21。

3.等于5

拟舍弃数字的最左一位数字等于5，而右面无数字或皆为0时，若所保留的末位数字为奇数（1、3、5、7、9）则进一，为偶数（0、2、4、6、8）则舍弃。

范例：拟修约数值0.35，修约间隔为0.1（10-1），因此修约值为4×10-1（特定时可以写为0.4）。拟修约数值2500，修约间隔为1000（103），因此修约值为2×103（特定时可以写为2000）。

4.负数

负数修约时，先将它的绝对值按上述规定进行修约，然后在修约值前面加上负号。

范例：拟修约数值-355，修约到十数位，修约值为-36×10（特定时可以写为-360）。拟修约数值-0.0365，修约到三位小数，即修约间隔为10-3，修约值为-36×10-3（特定时可以写为-0.036）。

5.不许连续修约

不许连续修约，也即拟修约数字应在确定修约位数后一次修约获得结果，而不得多次按上述规则连续修约。

范例：修约15.4546到整数位。正确的为15。不正确的为15.4546→15.455→15.46→15.5→16。

对于修约规则，总的一句话是：“四舍六入五考虑，五后非零应进一，五后皆零视前位，五前为偶应舍去，五前为奇则进一，整数修约原则同，不要连续作修约。”

练一练：

对下列数据进行修约。

（1）5.72671修约为整数；（2）16421修约为两位有效数字；

（3）17.569修约到一位小数；（4）-0.0355修约到三位小数。