控制电路的优化设计

开关电源属于闭环自动控制系统，从结构框图来看，它是由主电路和控制电路两大部分组成。主电路包括输入滤波整流稳压电路、逆变开关电路、输出滤波整流电路。控制电路包括：电压取样电路、误差放大及补偿网络电路、脉宽调制及驱动电路。误差放大及补偿网络具有深度负馈，对信号进行放大，其实质是DIP网络即微分、积分、比例补偿网络，它的作用为改善开关电源瞬态性能，所谓瞬态性能就是放大器的动态性能。

控制电路优化设计的主要任务是网络设计，内容是：选择DIP网络拓扑，选择、计算网络元件参数。方法是：采用最优控制理论与非线性规划结合的方法，建立新的数学模型，由计算机软件设计并演算出各种参数。

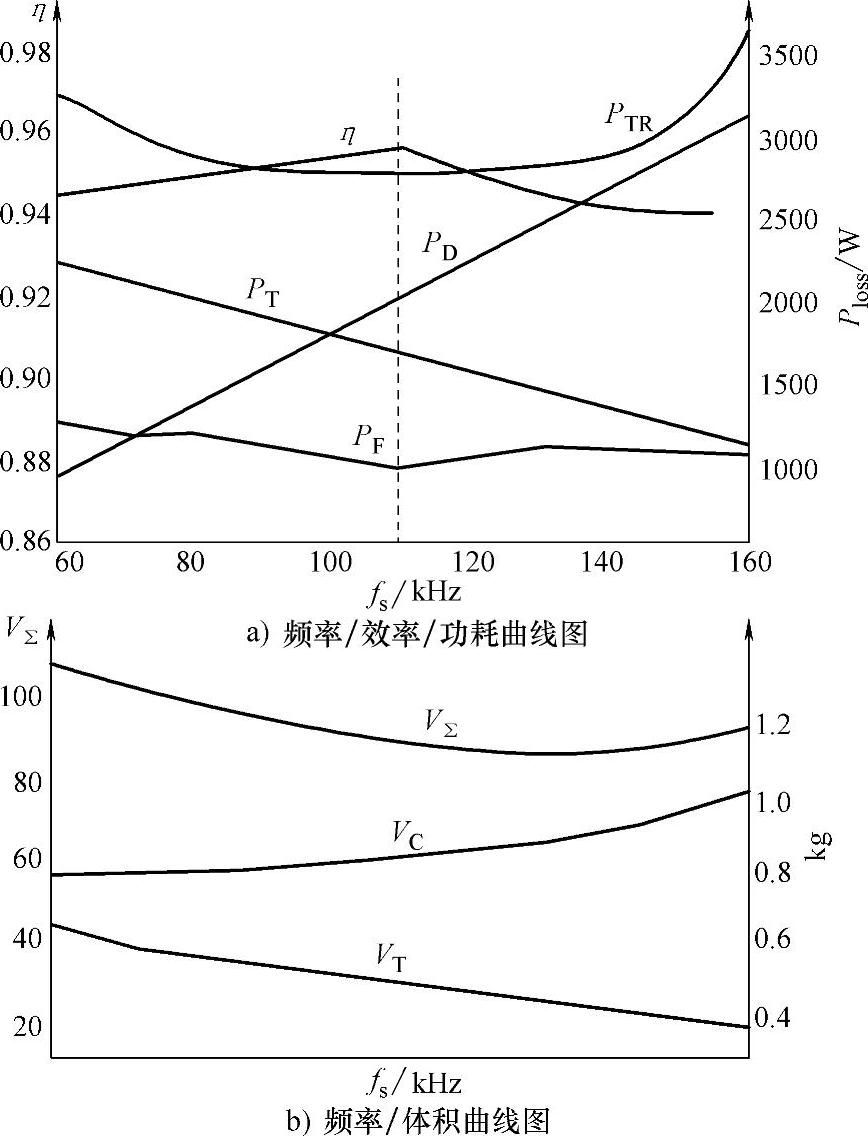
图6-20 全桥式变换电路优化设计结果曲线图

P_loss—功率损耗 V—体积 P—功率 V_∑—总体积 C—变换电路 T—变压器 D—二极管 η—效率 f_s—工作频率 TR—晶体管 F—散热器

开关电源应用了闭环自动控制理论，用动态分析的方法。为了解自动控制理论，对电源瞬态的基本概念进行分析。图6-21是开关电源瞬态响应特性响应时间曲线图，t_d为延迟时间、t_r为恢复时间，ΔV为输出电压从V_o1变化到V_o2允许带宽。图中的A为下冲、B为上冲、C为负冲。目前，瞬态分析有时域法和频域法两种。时域法是在图示仪上观测到的瞬态特性，如图6-21的波形根据A、B、C三点振幅进行分析，直观地观测到瞬态恢复时间，得到开关电源的开关速度、振荡频率、上冲及下冲幅值，还可以测量输入峰值电压和突变负载开关电源抗干扰的能力等。频域分析法是一种间接方法，是利用开关电源开环频率特性，间接地测定瞬态特性，图6-22是开关电源的波德（Bode）图，图上用增益裕量和相位裕量表示开电源的稳定时间。所谓相位裕量，是在相对频率-180°与幅频曲线相交线，再与相频曲线相交横坐标垂直向下与幅频曲线相交，幅频曲线上两交点的垂直距离为相位裕量。增益裕量是相频曲线跟横轴的交点，图6-22相频曲线图上的b点垂直向上与幅频曲线交点c。c点与幅频曲线的横轴之间距离为增益裕量。增益裕量应大于15dB。相位裕量表示开关电源的相对稳定性应大于45°。除此以外，开关电源瞬态特性指标还有恢复时间、上冲幅值、输入音频和负载音频扰动衰减率等。

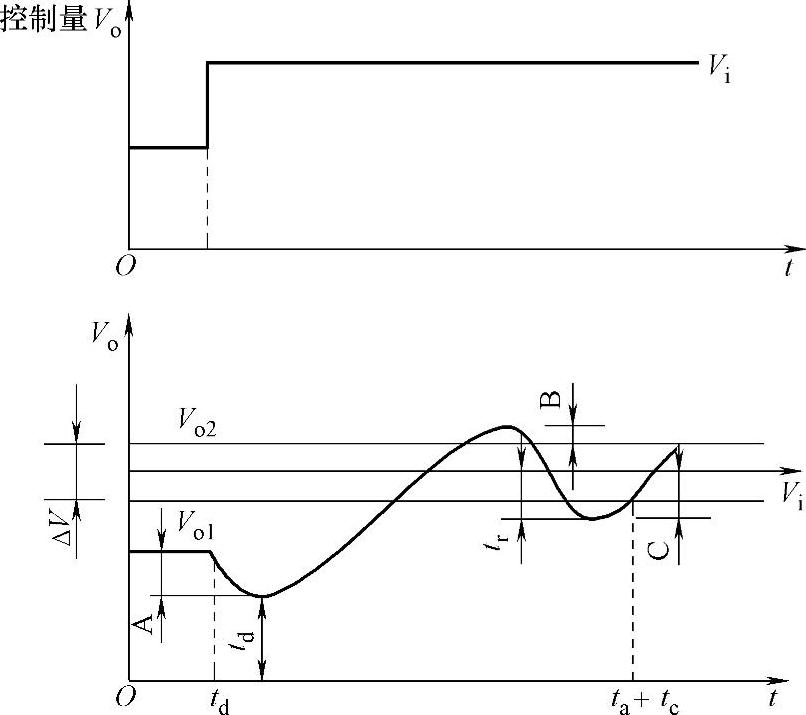
图6-21 开关电源瞬态响应特性曲线图

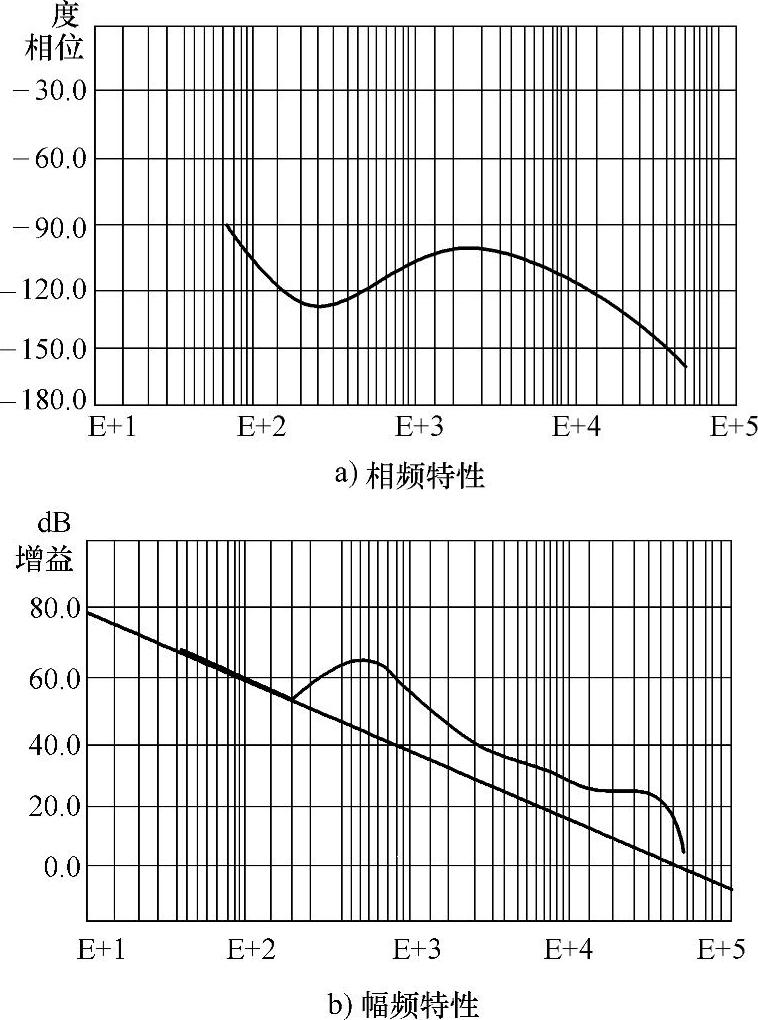
计算机通过数学模型软件不但可测定瞬态特性指标参数，还可以在屏幕上显示出开关电源反馈控制开环频率特性Bode图，图6-23a是相频特性曲线图，图6-23b是幅频特性曲线图。从这两条曲线上即可看出一台开关电源的稳定性和抗扰动能力，设计工程师可根据图形进行设计修改，这可对开关电源优化设计带来方便。

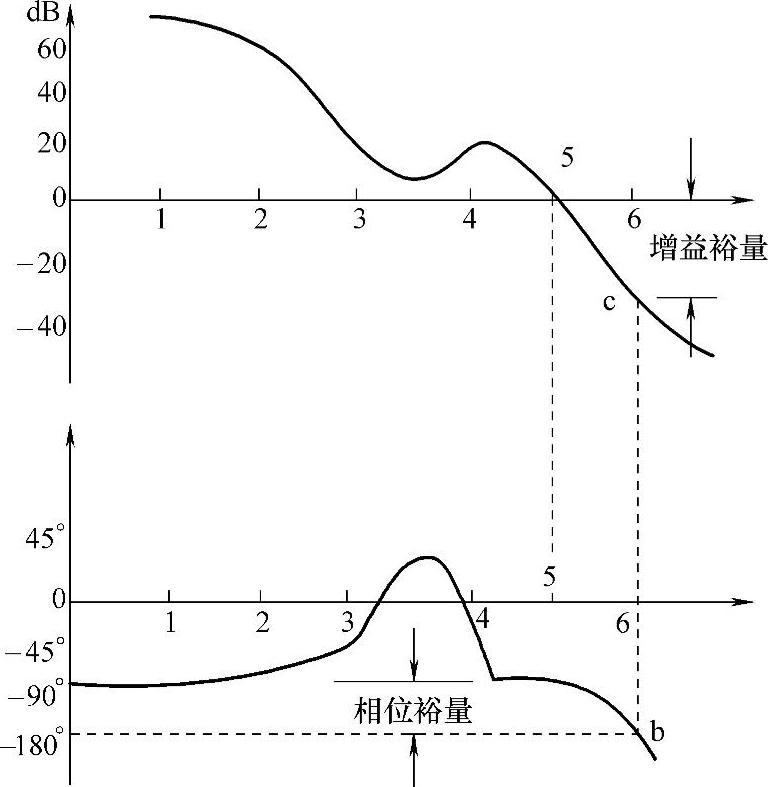
图6-22 开关电源开环幅频和相频特性曲线图

(www.xing528.com)

图6-23 开关电源开环频率特性曲线图

各项瞬态参数指标是确定控制反馈电路的依据，优化瞬态设计就是优化设计控制电路，一般采用非线性规划的方法。开关电源响应速度快，抗扰动能力强，是优化设计的目标，瞬态设计数学模型表达式为

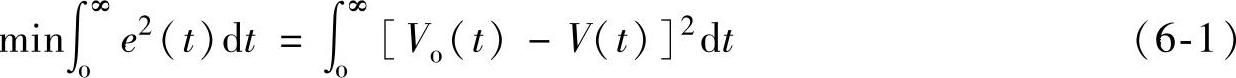
式中，min表示瞬态误差平方积分最小值；e（t）表示开关电源的瞬态误差。

误差二次方积分函数，实际上是开关电源闭环反馈频率特性的表达式。式（6-1）误差平方积分是利用时间微分来确认瞬态误差优化设计，式（6-2）是将时间微分转变到频域积分的表达式。

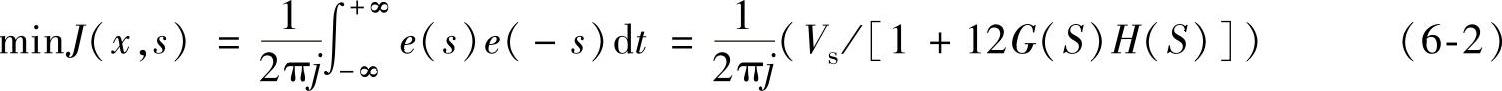
式中，e（s）为e（t）的拉氏变换系数，J（x，s）是频域ISE指标，H（S）=H₁（S）H₂（S）为补偿网络传递函数和补偿网络拓扑函数。J的表达解析式与开关电源的结构形式有关，如反激式比正激式J的有效值要高出10%，全桥式比反激式高5%左右，这是因为各种结构形式要求的上冲幅值、增益裕量和抗负载扰动等瞬态特性指标是不同的，这些只有通过计算机测定图形比较容易解决的。

瞬态设计数学表达式还可以通过计算机仿真完成对开关电源控制数据进行演算，要完成这一复杂过程，首先要将瞬态误差、负载变化、电源增益、工作频宽或是占空比变量、电压变量等各项参数输入式（6-1）和式（6-2）可以完成仿真操作。

解决仿真操作要建立电路仿真模型也就是软件包，上述瞬态设计表达式就是仿真模型的基础，有了列方程的方法，仿真程序的数据结构也基本确定，用牛顿法对方程进行消解。

开关电源中的反馈电路目前广泛使用集成电路控制芯片。