阶梯波技术：稳定输出电压的实现方式

尽管高频SPWM技术被认为是在中小功率变流器中抑制谐波失真的最好方法，但是对于大功率变流器而言，开关频率的限制和开关损耗的考虑往往限制了其可用的开关频率，从而减低了谐波抑制的效果。对于大功率变流器而言，利用多个桥的组合来提高装置的等效开关频率，及利用方波叠加的方式生成阶梯波，以逼近正弦波，均是目前得到广泛应用的更好的谐波消除方法。大量的研究表明，采用低开关频率的阶梯波变流器在同样的谐波水平下，在降低功耗、动态响应和器件利用率等性能方面均优于常规的采用高开关频率的SPWM变流器，因此采用阶梯波的变流器被作为应用于电力系统的大功率补偿装置的标准结构。

SPWM的根本思路是通过适当地选择开关器件的动作时刻，使调制波的脉冲宽度基本上呈正弦分布，即各脉冲与正弦曲线下对应的面积近似成正比，并使输出信号中最低次的谐波频率为载波频率的整倍数。这种技术以增加了控制的复杂性和减低了变流器的效率为代价，来抑制低次谐波对系统的影响。

阶梯波技术的根本思路则是利用一系列方波信号的和所组成等阶梯波来逼近正弦波。显然，随着参与合成的方波数量的增加，输出波形所含的阶梯数增加，可以有效地抑制了输出波形中的谐波分量。理论上，当阶梯波的阶数趋于无穷时，就可以实现一个理想的正弦输出。通过实践，各国技术人员提出了许多实现上述阶梯波的方法，这里仅对两种应用最广的方法加以说明：一种通常称为多电平（Multi-level）方法，其特点在于其直流侧具有一系列串联的直流电源，而阶梯波是通过对该多电平直流电压进行综合生成的；另一种则称为多脉冲（Multi-pulse）方法，其交流侧输出的阶梯波是将若干个桥输出的方波信号通过变压器进行耦合生成的。下面分别加以说明。

1.多电平变流器（Multi-levelconverter）

多电平变流器的思想最早是由日本科学家Nabel等人于1981年提出的。它的主要思路是通过精心设计，将变流器的输出电压由传统的两电平变为多电平，从而利用阶梯波去逼近正弦输出电压^[7]。这种多电平变流器作为一种新型的高压大功率变流器，从电路拓扑结构入手，在得到高质量的输出波形的同时，由于不需采用输出变压器和动态均压电路，开关频率低，从而达到了开关器件所承受的电压应力小、效率高的目标。

为了便于说明，下面对普通三电平变流器和常规两电平变流器加以比较。

三电平变流器的主要优点是相对于两电平变流器而言，为输出电压的控制提供了一个附加的自由度。由图6-15中相应的信号波形可以看到，所谓两电平变流器，其输出仅含+E_d和-E_d两个电平，在一个周期中开关器件的导通角被固定为180°，因此对其输出电压的幅值和谐波含量的控制只能通过在方波中开口（即利用正弦脉宽调制或所谓优化PWM）实现。而三电平变流器的输出的电压包括+E_d、0、-E_d三个电平，输出脉冲的宽度是可以通过改变变流器输出端处于零电平的时间来加以调节的，这就为变流器增加了一个对于输出电压的幅值和频谱加以控制的手段。

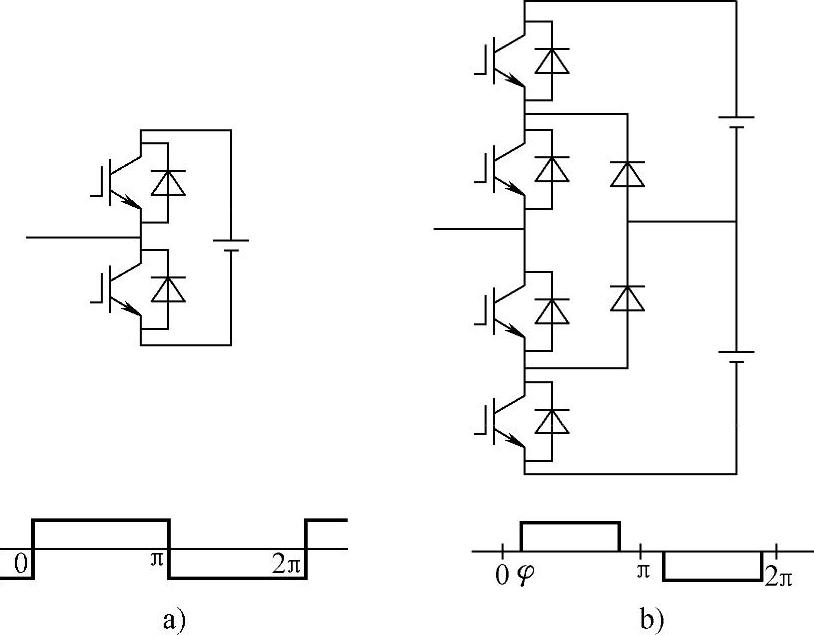
图6-15 两电平和三电平变流器电路原理图

a）两电平 b）三电平

假定方波脉冲的相移为ϕ，即脉宽为π-2ϕ的电压n次谐波有效值为

而线电压的n次谐波有效值为

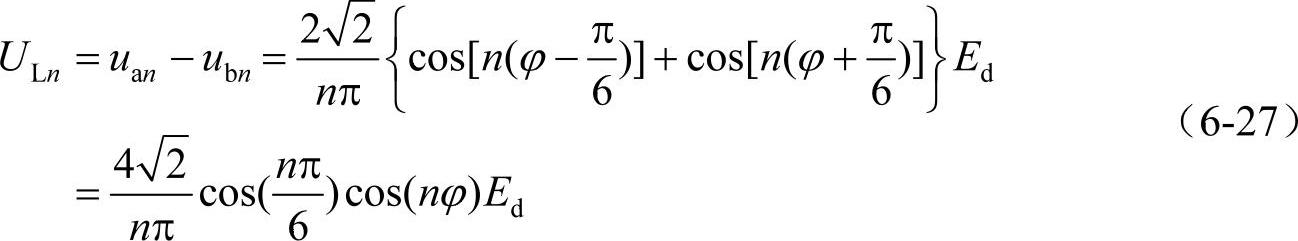
其基频电压的有效值为

在ϕ=0时，其基频有效值为常规两电平变流器的两倍，但三电平变流器所用开关器件的数量相当于两电平变流器的两倍，所以从电压和电流利用率来说是相当的，但由于此时每个器件的电位均被二极管钳位于直流电压的一半，所以不需通过复杂的动静态均压电路就可以达到常规器件串联的效果，这是多电平变流器受到青睐的一个重要原因。此外，由于各次谐波的有效值是相应余弦的函数，因此就可以通过调节触发角而令相应的余弦函数为零来达到消除某次谐波的目的。比如，希望消除n次谐波，则可以令触发角ϕ=90/n，此时相应的谐波含量将为零。比如为了消除11次谐波，可以令ϕ=8.18°即可。

多电平变流器正是在三电平的基础上构成的。注意到如图6-16所示的矩形波的傅里叶级数可以表示为

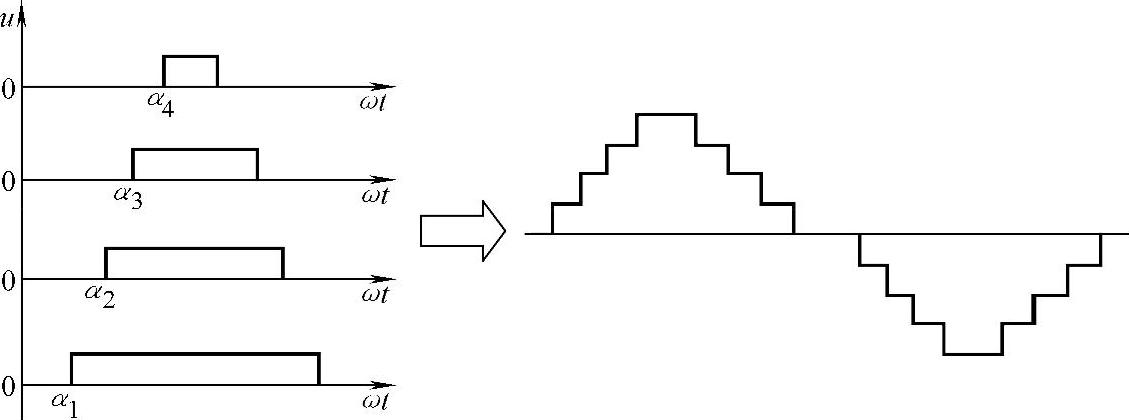
图6-16 等阶梯波生成原理示意图

对于M电平变流器，输出电压的傅里叶展开式为

式中，下角s为单相桥的数量，s=（M-1）/2。

因为每个模块均是独立的单相桥，并且其输出可以独立控制，因此M电平变流器具有s个自由度，这既可以用来控制输出电压的幅度，又可以通过仔细安排每个模块的触发时刻，使某次谐波的系数，来消除选定的n次谐波。比如对于两个三电平变流器，如希望消除5次谐波，则cos5ϕ₁+cos5ϕ₂=0。一个简单的解法就是令5（ϕ₁+ϕ₂）=180°，得到ϕ₂=36°-ϕ₁，即如ϕ₁=10°，则ϕ₂=26°。

多电平变流器从提出至今，出现了许多不同的电路拓扑，但归纳起来主要有三种，即二极管钳位型（Diode clamp）、飞跨电容型（Flying Capacitor）和采用独立直流电源的级联型（Cascade）。它们的结构分别如图6-17a、b、c所示。

它们的共同优点是：①随着电平数的增加，如图6-17a所示，输出波形逼近正弦，输出电压和电流的谐波含量明显降低；②器件开关频率低，开关损耗小；③由于器件两端电压被钳位于一定的电位，无须均压电路，器件所承受的应力小。

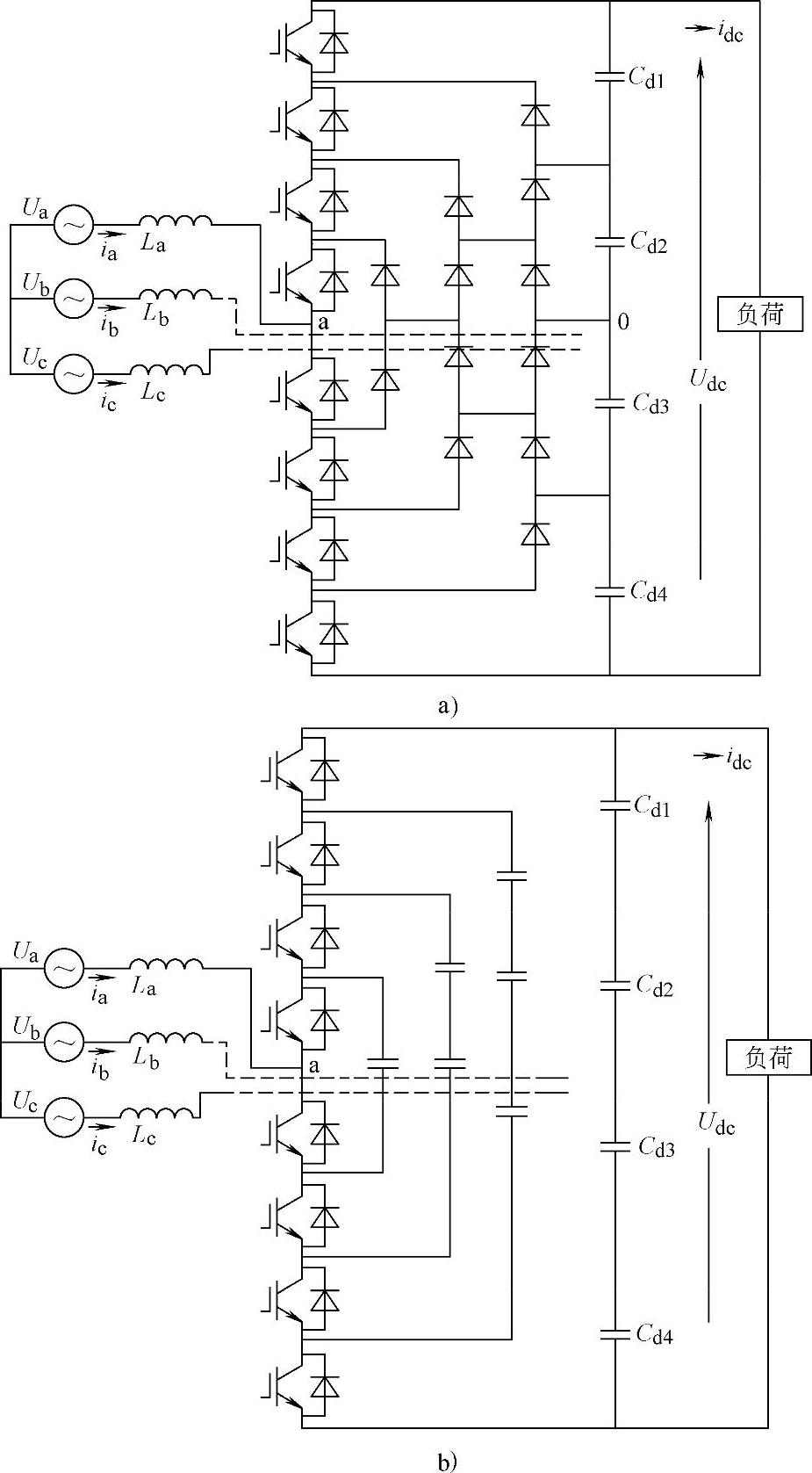
图6-17 多电平变流器

a）二极管嵌位式 b）飞跨电容式

图6-17 多电平变流器（续）

c）级联式

但这三种电路又有各自的缺点，下面分别加以讨论。图6-17a给出了一个常规的、具有钳位二极管的多电平变流器的结构图，这可以看做是常用的三电平变流器的直接延伸。阶梯波电压是通过对一组串联的、相位相同，但脉宽不同的方波进行综合生成的。一个所谓的M电平二极管钳位式变流器，通常由M-1个串联电容，由分别包括M-1个串联等效开关的正组和负组组合而成的桥臂和相应的钳位二极管构成，其输出的相电压具有M个电平，而输出的线电压由于是由一相的正组产生的电压和另一相的负组产生的电压组合而成，所以具有（2M-1）个电平。显然，随着电平数的增加，合成后的输出波形的阶梯数也增加，谐波含量也随之降低，同时，由于在钳位二极管的作用下，相互串联的器件被钳位在相应的电容电压，这意味着可以在不需考虑串联器件均压问题的条件下，通过增加变流器的电平数达到高压运行。理论上，常规的三电平变流器的原理完全可以推广到多电平变流器中，但实际上，由于下述原因，五电平以上的变流器很少在实践中得到应用。

1）对于三相桥变流器而言，每增加一个电平需增加6只钳位二极管，并且所增加的钳位二极管所承受的反向阻断电压的随电平数的增加而增加，如果以三电平时二极管的阻断能力为单位，则三相桥实际所需钳位二极管的数量将是3（M-1）（M-2），即随电平数的二次方增加。这不仅使变流器的结构变得十分复杂，同时也使得过高电平数的变流器变得不实际。

2）每个局部电容上所承受的平均电压必须相等，以消除输出交流电压中所可能出现的直流分量，但当变流器和系统之间交换有功功率时，由于不同电平的方波脉宽不同，从而导致每个电容的充放电时间不同，也即与系统交换的有功能量不同，如果不加控制，必然造成不同电平之间的电容电压不等，上述问题进一步增加了控制的复杂性。到目前为止，实践中已实现的变流器的最高电平数为9。

飞跨电容式变流器，如图6-17b所示，和钳位二极管式有相似的结构和性能。它们同样可以通过增加电平的级数来减小输出电压的谐波含量，利用电容分压实现对开关器件钳位的目的，从而免除了对串联器件进行动静态均压的要求。但也和钳位二极管式变流器相同，除了要解决在进行有功功率交换时各级电压的平衡问题外，另一个重要的问题是为了抑制变流器工作中出现的电压脉动和进行分压，所需电容器的数量和容量均较大。假定每个电容的耐压水平和主开关所用电容相等的条件下，为了实现M电平变流器，每个臂需要（M-1）（M-2）/2个均压电容，这同样使得过高的电平级数成为不可能。太原钢厂于2001年由ALSTHOM公司引进的轧机中所采用的四电平变流器就采用了上述结构，但总的而言，在多电平变流器中，采用飞跨电容式结构的装置数量较少。

如上所述，直流侧分压电容电压不均衡问题是困扰上述两种变流器的一个重要问题，一个显而易见的解决方案就是利用直流电源来代替储能电容，从而使直流侧电压自动实现平衡，问题是在变流器中引入多路独立的直流电源，在实践中将造成结构的复杂化，是相当困难的。

图6-17c所示的所谓级联式变流器是其中一个成功的事例^[5，6]。由于它不需要前两种电路所需的大量钳位二极管和钳位电容，易于封装。同时，由于它的基本组成单元为传统的两电平单相全桥变流器，故结构简单，技术成熟，易于模块化。由于产生级联式变流器中，每个单相逆变单元都有独立的、电压为U_dc的直流电源，而每个单相逆变单元分别可以输出+U_dc、0、-U_dc三种电平，将上述单相逆变器进行串联，就可以使输出的电压叠加，构成多级电平，而通过控制每一级逆变器的导通角，就可以控制相应的输出电压的宽度，也即输出交流电压的PWM波形。

设逆变单元串联级数为N，则输出相电压的电平数定义为m=2N+1。图6-18a与b分别给出由输出电压为九电平的级联式和二极管钳位式两种变流器所构成的单相桥结构图。虽然从图上观察，二极管钳位式变流器所用器件比级联式要多，比如钳位二极管，但实际上级联式独立电源通常需分别由变压器不同绕组所提供的交流电压经整流后得到，所以结构上远比前者要复杂。此外，由于电路结构上的原因，级联式不能简单地利用三个桥臂实现三相变流电路，而需利用三个单相桥组来实现，这导致所需器件数量大幅度增加，也是对其使用的一个限制。但由于它可以方便地实现级联而不需考虑各级电容的均压问题，所以得到越来越广泛的关注和应用。

值得指出的是，当利用其作为无功补偿装置时，由于变流器本身不与系统交换有功能量，因此一个周期中电容充放电的能量相等，各级电容电压的平均值将维持在预置值的附近，可以直接利用电容来提供变流器工作所需的直流支撑，而不需额外的独立电源，从而大大地简化了变流器的结构。比如ALSTHOM公司于1997年开发的75MVA静止同步补偿器中就采用了由7个独立单相桥串联而成的15电平的级联式变流器结构，取得了良好的效果。

图6-18 九电平变流器

a）H桥构成 b）二极管嵌位式

但由于级联式变流器基于单相桥变流器，和常规的三相桥同步补偿器不同，虽然每个直流电容在一个周期中吸收的有功功率为零，但注入电容的瞬时有功功率却不为零。这将导致电容电压的波动，这就要求采用容量较大的直流中间电容，这也是此类变流器的一个缺点。

综合而言，和其他多电平电路相比，级联式（也称链式）电路有如下优点：

1）由于电路由相同的单相桥构成，所以只需增加串联的级数即可增加装置的容量，原则上不存在可以实现的电平数的限制。

2）每个单相桥具有其独立的直流电源，并且每个模块中的所有器件均被钳位于该直流电压，所以不需额外考虑电压均衡问题，也不需要额外的钳位二极管和飞跨电容。

3）单相结构为三相不平衡控制提供了可能。

由于每个模块均是独立的单相桥，其输出电压可以自由控制，因此一个M电平的变流器具有（M-1）/2个自由度，可以用来通过控制每个模块的导通时间控制输出电压的幅值和/或消除特定的谐波。尽管多电平波形也可以通过对两电平方波进行移相后叠加生成，但为了便于控制，一般多采用脉宽不同的方波叠加而成。但不同的脉宽带来一个直接的问题就是不同电平的开关器件的负荷率不同，从而减低了器件的利用率。

多电平变流器通常只需通过一个常规的降压变压器和系统实现互连，相对于多脉冲变流器而言，免除了体积庞大、结构复杂、昂贵、低效和具有难以控制的非线性磁化的曲折型变压器，所以不论在占地面积，还是造价上均具有一定的优势。

2.多脉冲变流器（Multi-pulse converter）

多脉冲变流器的基本结构就是将若干个基本的变流器通过变压器进行适当的串联或并联构成的。与多电平变流器相同，其输出电压也是通过将一系列分布的方波（或准方波）信号叠加而成的阶梯波，与前者不同的是，这些参与综合的两电平的方波信号具有相同的脉宽和幅值，只是相互之间具有适当的相移。根据方波信号相互之间的相移不同，上述变流器具有不同的结构，因此其合成的波形中的谐波含量也有不同。但总的而言，多脉冲技术可以在大功率开关器件工作频率较低的情况下通过变流器的相继触发提高了变流器组的等效开关频率，从而提高了变流器的响应速度和谐波抑制效果。

在实际应用中，多脉冲技术有两种基本类型：一种是所谓的谐波中和（Neutralization）技术，它采用所谓的“全相位组”（Complete Phase Sets）技术，即利用若干个经变压器耦合的变流器机组所输出的方波波形之间和与其对应的变压器输出入绕组之间所存在的均匀相移来达到谐波抵消的目的，通常也称为多重化技术。这种方式又可以进一步分为采用一组以曲折方式连接的变压器和其对应的变流器组组成；通过将上述变流器输出的方波在电路中，比如在交流线路侧进行综合来生成所需的阶梯波，和利用一个三绕组变压器，在变流器侧的两个绕组分别接成星形和三角形联结，利用两个变流器生成的方波信号在磁路中进行叠加，从而在二次侧生成相应的阶梯波。第二种为移相式谐波抵消（Phase-shift Harmonic Canceling）技术，它利用对变流器的触发信号进行适当的控制生成相互之间存在所需相移的一系列方波信号，然后通过常规变压器在交流侧进行综合，实现消除所定谐波的目的。下面分别加以介绍。

（1）多重化方法 多重化技术的主要特点是进行合成的所有方波信号的幅值相等，并且相互之间的相移也是均匀的，从而构成所谓“全相位组”。图6-19所示为一个M重三相变流器的原理图，它包括M个三相变流器组，每个变流器组由结构相同的变流器和与之所需的相移对应的曲折变压器构成。变流器通过在交流侧以串联（见图6-19a）或并联方式（见图6-19b）曲折连接的变压器将各变流器组输出电压进行综合后输出，而在直流侧，变流器组同样通过串联或并联方式（多采用并联）连接，从直流侧吸收电能。

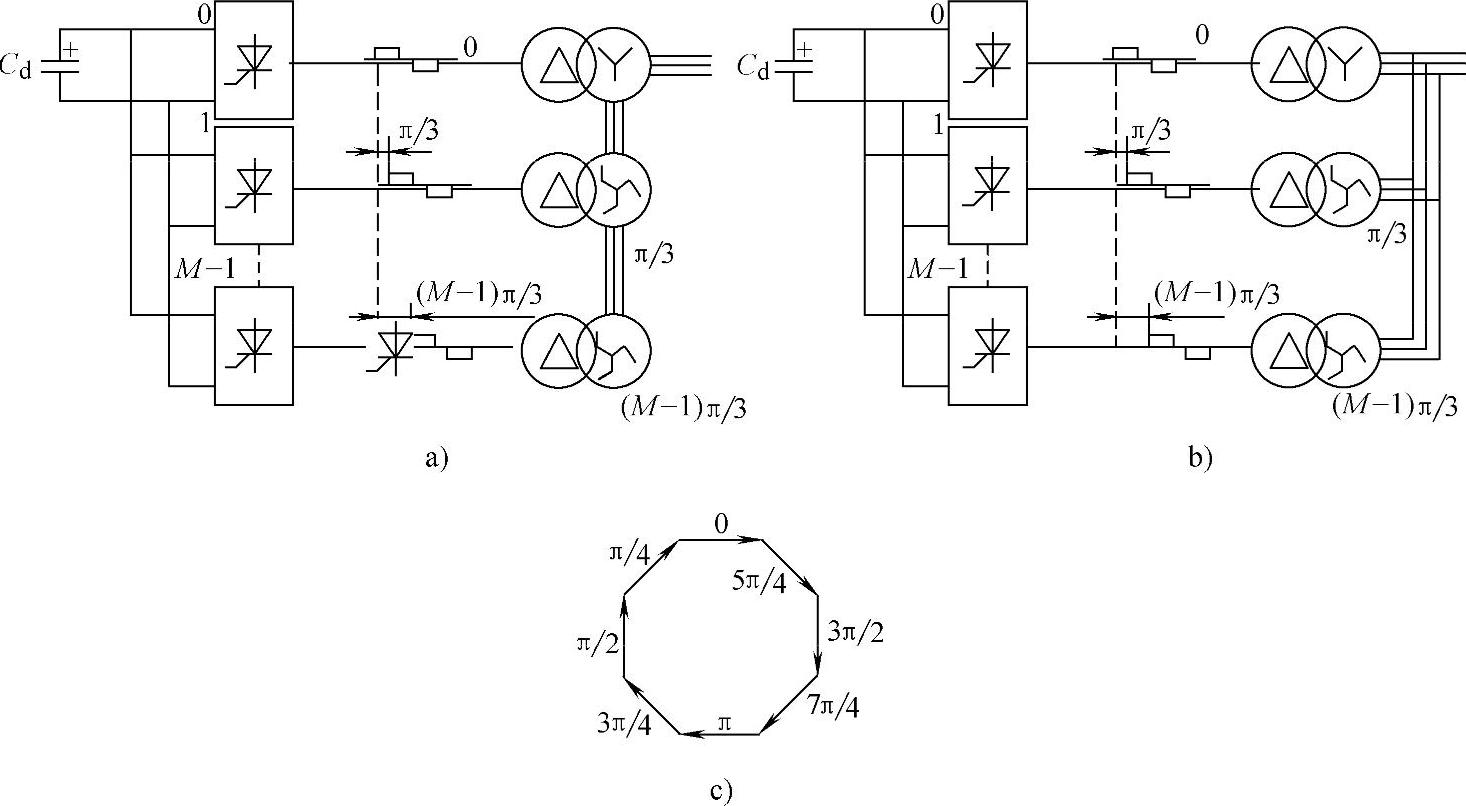
图6-19 M重多脉冲变流器电路图和谐波合成图

a）串联多脉冲变流器 b）并联多脉冲变流器 c）电压相量合成

如对图6-19中的变流器组分别命名为0～M-1号，为了实现消除谐波的目的，M个变流器组在相位上均匀分布，即每个变流器产生的方波信号的前沿在相位上较其前一个变流器输出的方波信号的前沿滞后π/（3M），而为了便于交流侧基频信号合成，则利用曲折变压器，使后一个变流器组的变压器的相位较前一个变流器组超前π/（3M），从而使交流侧生成的M个方波的基频相位相同。但由于上述结构对不同，谐波产生的相移也各不相同，所以经叠加后，谐波信号不能完全抵消。下面对此进行详细的讨论。

众所周知，一个三相桥变流器输出的电压波形中所含谐波的次数可以用下式给出：

n=6r±1 （6-31）

尽管在多脉冲变流器中，变流器在交流侧既可以采用串联，也可以采用并联方式连接，但实际中多采用串联连接的方式，下面就以此为例进行讨论。

假定变流器由M个结构和输出脉冲宽度相同的两电平变流器组组成，并分别标为0～M-1号。为了便于讨论，以0号变流器直流侧方波脉冲的基频分量的过零点作为参考点，此时方波脉冲为奇函数。为了实现消除谐波的目的，第0号变流器的触发信号应保证其生成的方波信号的基频分量经变压器输出后与交流侧参考电压的相位相同。第1号变流器直流触发信号前沿的相位则滞后第0号变流器（60/M）°；同时为了保证在交流侧其输出的方波信号的基频分量和第0号变流器输出信号的基频分量（也即交流参考信号）同相位，则需要利用变压器将该基频信号的相位向前移相应的角度为（60/M）°。注意到变流器输出电压的谐波中n=6r+1次谐波为正序谐波，而第1号变流器方波信号前沿滞后（60/M）°，意味着该信号中所含的n次谐波相量比第0号变流器的同次谐波相量滞后（60×n/M）°，再注意到由于变压器结构上的变化所引起的相移对于各次谐波而言是相同的，即均超前（60/M）°，因此该变流机组输出的交流电压中n次谐波较之第0号变流器组同次谐波的相位将滞后：

而由于n=6r-1次谐波是负序分量，所以对于正序分量而言超前（60/M）°的变压器结构，对于负序分量相当于同等角度的滞后，这样第2号变流器组中n=6r-1次谐波相量较之第1号变流器同次谐波相量的相位滞后为

据此可以类推，M重变流器中，第k个变流器组较之k-1个变流器组变流器侧方波信号的前沿滞后（60/M）°，再经曲折变压器的超前（60/M）°变换，相邻两变流器组输出电压中所含的基频分量相位相同，第k-1台和第k台变流器输出的n次谐波分别较第0号变流器组滞后2（k-1）πr/M（rad）和2kπr/M（rad），即后者的相位滞后前者2πr/M。将上述关系推广到整个变流器，可以得到在一个周期中均匀分布的M个同次谐波相量的相位分别为

0，2πr/M，4πr/M，…，2（M-1）πr/M

注意到上述相位之间所存在的循环特性，故上述M个相位就构成了所谓的“完全相位组（集）”。(www.xing528.com)

据此，等脉宽的参考方波逆变器的输出中，除了基频信号以外的谐波量可以用公式表示为

式中，θ为脉宽，对于180°导通型，θ=π。

假定变流系统包括M台结构和输出脉宽相同的变流器，分别记为0～M-1号，以第0号变流器作为相位参考，其他各台顺序滞后2π/M（rad）。由此可以得到，第k台变流器输出方波的谐波分量可以表示为

对上述M台变流器组合而成的变流装置的输出波形进行线性组合，则得到合成信号的谐波分量为

因为表示谐波次数的n和表示变流器顺序的k是两个独立变量，所以改变两者的求和顺序并不影响其结果，因此可以交换其求和顺序，而得到输出信号中n次谐波的含量为

上式为一个包括M项的几何级数，其中和式中各项构成了上述“完全相位集”，定义r=pM，则可以将求和号中各项展开得到

当参数r是M的整倍数时，即p为整数时，各项之间的相移为周期的整倍数，故

S_n=Mcosnωt （6-39）

当p不是整数时，等式两边乘一个系数2sinpπ，根据三角函数积化和差可以得到

故

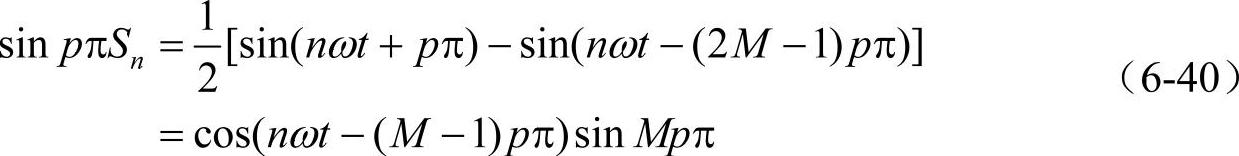
而由于r=Mp是整数，所以可以得到

即当p不是整数时，上述各项的和为0。对于n=6r+1即正序分量时，可以得到同样结论。因此，在采用上述多重化的结构后，所有谐波次数n=6r±1中，r不为重数M的整倍数的谐波均被抵消，输出中仅含参数r/M为整数的分量。实际上，当r为M的整倍数时，M个变流器组所输出的n次谐波的相位相同，所以综合后的信号幅值将为各变流器组该次谐波幅值之和。而当r/M不是整数时，不同变流器组输出的n次谐波相量之间将存在相位差。作为M重变流器，由于各变流器组输出的同次谐波的幅值相

同，而谐波相量之间以（360×）°的相位差均匀分布，所以M个变流器组的对应谐波相量将构成一个封闭的正多边形。图6-19c所示即为一个8重化变流器的29次谐波（即r=5）的合成相量图。作为8重化变流器，各变流器组直流侧触发脉冲和交流侧变压器之间的相移均为（60/M）°=7.5°；相应地其直流侧29次谐波之间的相移为（7.5×29）°=217.5°；再加上变压器7.5°的附加相移，总共相移为225°。8个长度相同、相互之间相移为225°的相量相加，在平面上构成一个正八边形。上述封闭的曲线表明，该次谐波的相量和为零，这个结论可以推广到所有r/M不为整数时的情况：即当三相M重变流器的特征谐波中所有r/M不为整数的谐波均在交流侧被抵消。再考虑到当r/M是整数时输出谐波将被叠加这个事实，可以看到，M重变流器的第一个显著优点是可以同时消除所含谐波次数总量的（M-1）M，换句话说，可以使装置输出信号中谐波次数减低为原来的1M。比如，常规的12脉冲TCR的变压器采用两个二次绕组，一个接成星形联结，另一个接成三角形联结。此时，假定变压器一次绕组为星形联结，则三角形联结变压器的输出信号相位将超前输入信号30°，如相应地令该变流器的触发脉冲滞后星形联结变压器所接变流器的触发脉冲30°，则构成一个两重化（即M=2）的变流器，其中所有r为奇数次的谐波均被消除，即除了三相变流器的特征谐波5、7次谐波外，所有与其相差为12的整倍数的谐波[也称其循环谐波，6（2p+1）±1]均被同时消除。显然，较之其他谐波抵消方式而言，多重化是一种更为有效的谐波消除方法。随之而来的另一个优点则是M重变流器作为6M脉冲装置，其产生的最低次谐波为6M-1次。

问题在于产生上述所希望的任意相移必须采用曲折变压器实现所需的均匀相移才能实现，而采用曲折变压器除了变压器本身结构复杂外，也使得系统的接线变得十分复杂。此外，曲折变压器较之普通变压器大致要多用15%的导体，导致体积和价格的增加。更为重要的是，随着重数增加，谐波消除的效率急剧下降。分析指出，M重化可以消去的谐波次数占总谐波次数的比例为（M-1）/M；而当重数由M增加为M+1时，所额外消除的谐波次数仅占M/（M+1）-（M-1）/M=1/[M（M+1）]。比如两重化可以消除50%的谐波次数，而三重化则消除66.7%的谐波次数，即新增等一重化变流器仅消除了16.7%的谐波次数。但两重化可以借助常规的星-三角变压器实现，但三重化则必须采用曲折变压器。所以，过多的重数，不论从经济上还是技术上均是不合理的，目前的趋势是尽可能采用普通的变压器实现两重化的结构，然后辅之以其他技术，如下节介绍的相移抵消法，来进一步减低谐波。

在理论上，在交流侧对各个变压器组产生的方波信号进行串联或并联合成均可以达到多重化消谐的目的。并联接法的一个显著优点是一旦某台变压器组出现故障，可以仅令故障变压器组退出运行，而其他变压器组仍可正常运行。但采用并联接法时由于各个变流器组输出的电压波形各不相同，将在输出变压器之间引起环流，为了对其进行抑制，通常需增大变压器的漏抗或插入限流电抗，这增加了结构的复杂程度，同时还将引起附加损耗。此外，输出侧采用并联连接时，耦合电抗必须面对每个单元变流器所产生的全部谐波分量；而串联连接时，由于通过谐波消除技术，流经变压器的仅是未能消除的谐波含量，因此可以采用较小的连接电抗，所以在目前广泛采用的电压型变换电路中，通常都采用变流器在直流侧并联，而变压器二次绕组在交流侧串联的多重化方式。

实际应用中，除了上述利用串联或并联变压器在电气上实现耦合的多重化结构外，还有一种利用磁路实现耦合的所谓“变压器铁心耦合”的多重化结构。图6-20所示即为一个二重化铁心耦合的电路，该方法由于采用一个三绕组变压器来实现二重化所以交流侧电路得到了简化。但由于其变压器阀侧绕组中存在5、7、17、19等次谐波，故需在直流侧串入电抗，以抑制谐波，其效果与常规两重化变流器大体相当。

图6-20 铁心耦合二重化多脉冲变流器

（2）移相抵消技术（Phase-shift harmonic canceling）上述多重化的方式虽然在谐波消除方面具有极高的效率，但除了可以利用星形联结和三角形联结实现两重化外，必须采用复杂的曲折变压器来实现多重化的目的。实践中存在一个问题，是否可以仅通过增加并联的变流器数在加大装置容量的同时，也达到消除谐波的目的？回答是肯定的。通过控制并联变流器所产生的方波之间的相移，同样可以达到消除或抑制某些特定谐波的目的。

实际上，两列脉宽和幅值等同的方波信号基频分量之间的相移，等于两列方波信号前沿之间的相移，而对应的n次谐波的之间的相移，则是基频信号相移的n倍，见图6-21c。即如果第二个变流器输出的方波脉冲的前沿滞后第一个变流器ϕ，则其输出信号的n次谐波相量将滞后第一个变流器相应谐波相量nϕ。因此假定令

nϕ=180° （6-42）

则由于两个变流器输出方波信号的幅值相同，故经过相应的变压器后，第二台变流器在交流侧呈现的n次谐波相量的幅值与第一台相同，但方向相反，即将互相抵消，成为一个十分有效的谐波消除方法。假定出于某种原因，如系统谐振等，希望消除11次谐波，根据上式可以得到所需的方波信号之间的相移为16.3°。在原则上，该方法可以用来消除任意次谐波，但应当指出的是，这种方法存在一些明显的缺点，一是如图6-21所示，为了在M重结构中消除某次谐波，必须在每一重均引入相应的“移相消谐对”，即消除一次谐波需有2M台变流器。由于消除某一个特定谐波需要两个结构完全相同的方波信号，而如希望在消去前一次谐波的基础上消除另一次谐波，则需另外增加两个结构完全相同的方波形成两组方波，组内的两个方波之间保持为消除第一个谐波所需的相移，而组间的方波信号相移则根据消除第二个谐波来确定。希望消除三个谐波时，则需将上述两组方波看作一个单元，再增加一个结构相同等单元。由此类推，如希望用移相消谐法消除n个谐波，则需要2ⁿ个变流器组，显然当所需消除的谐波次数多时，上述方法是十分不经济的。

图6-21 移相抵消式谐波消除技术

a）24脉冲变流器 b）变流器输出电压波形 c）相量图

此外，这种方法的另一个缺点就是，相对于作为基准的参考电压而言，合成后的电压的相位将向后移ϕ/2；在进行控制设计时，必须将上述滞后考虑在内，否则在和电力系统并网时，将可能由于变流器输出电压的基频分量和电源电压之间不同步，造成很大的电流冲击。

实践中，最常用的移相谐波抵消法，就是如图6-21a所示的所谓24脉冲变流器。外观上它和四重化变流器具有十分相近的结构，其中变流器组可以按变压器是星形联结还是三角形联结分为Ⅰ、Ⅱ，即0°和15°与30°和45°两个变流器组。两组之间实际上采用的是两重化技术，即变压器和变流器方波前沿触发信号之间的相位差为30°，从而可以消除5、7次谐波和其相应的循环谐波。但不同的是，每组中的两个变压器采用了相同的结构，仅是方波触发信号之间相差一个预定的角度，该角度可以采用均匀分布或消除某次特定谐波等要求来确定。比如图中第一组两个变流器的触发信号之间的相位差为15°，分别记为0°和15°变流器。上述两个变流器输出基频信号的相位差和方波信号的相位差相同，而幅值相同，故合成的基频信号U_I相当于二者的相量和，即幅值为U_I，1=2cos（15°/2）=1.98pu，滞后0°桥7.5°。而两个桥11次的相位差将分别为ϕ=11×15°=165°，合成相量为U_I，11=2cos（165°/2）=0.26pu；而13次谐波的相位差为ϕ=13×15°=195°，和U_I，13=-2cos（195°/2）=-0.26pu。利用这种方法进行方波合成，基频幅值近似等于单个方波的一倍，而11与13次谐波却仅为原单个变流器相应谐波的14，显然也是一种有效的谐波抑制方法。

实际中，变流器组间相移等角度是根据实际情况确定，比如系统中存在某次谐波振荡的可能时，采用谐波对消的方法显然是有利的，但由于均匀相移控制上比较容易实现，同时对构成谐波衰减较为均匀，故采用的较多。从谐波总含量而言，应当说两者相当，以固定脉宽为120°的两列方波叠加而言，采用谐波抵消（移相16.36°以消除11次谐波）时，谐波含量为6.805%；采用均匀相移（移相15°）时，为6.806%，较之简单并联叠加时的谐波含量18.12%减低了70%，所以均是十分有效的措施。

值得注意的是，上述方法虽然可以有效地抑制或消除某次谐波，并且在结构上和多重化相似，均是将若干个相同的变流器经耦合变压器相并联，但由于没有采用相应的变压器来实现所谓的“全相位组”，所以不能同时消除M-1次谐波和相应的循环谐波。因此从严格意义上讲，它不应称作多重化，比如常用24脉冲变流器应为4桥两重化变流器。较之多重化方法，每增加一重可以消除两个特征谐波及与之对应的循环谐波，移相消谐法每消除一次谐波需将变流器增加一倍，显然是相当不经济的，所以尽管结构简单，但除了上述特殊结构外，应用得并不广泛。

此外，虽然交流侧采用三角形联结可以抑制注入系统的3次谐波，但由于变流器中可能产生的3次谐波将在三角形联结绕组中形成环流，从而增大器件所承受的应力。因此在采用三单相桥结构或三相桥运行时，在系统不对称条件下，变压器应尽可能采用星形联结。

从上述对常用的阶梯波变流器的结构的介绍可以看到，随着阶梯数的增加，上述任一种的电压波形均将趋于正弦波。实践中，虽然多脉冲变流器需要采用体积庞大、价格昂贵、效率较低的变压器，但由于它提供了最有效的谐波消除方法，并且便于对输出电压进行控制，所以仍是高压大功率变流器中最广泛应用的谐波抑制方法。因此除非系统有特殊的要求，多脉冲方法仍是首选的方案。

（3）混合H桥多电平变流器 近年来出现了一类新的统称为混合H桥多电平变流器。它们虽然同样在负荷侧采用变压器耦合，但其特点在于变流器共用一个直流电源，而利用通过相应绕组的电流在磁路中的合成达到抑制谐波的目的。图6-22给出了其中一种结构和相应的输出波形。

图6-22 H桥混合变流器

a）H桥混合变流器的结构和输出波形 b）简化两电平H桥混合变流器

如图6-22所示，设u₀为负荷电动势，u_a、u_b分别为变压器T_a、T_b二次电动势，N_a和N_b分别为变压器T_a、T_b的一二次匝数比，设N_b：N_a=n，有下式成立：

u₀=u_a+u_b=（k_an+k_b）E_d （6-43）

式中，k_a为变流器a的工作状态值，当变流器输出电压为正时，k_a为1，当输出电压为零时，k_a为0，当输出电压为负时，k_a为-1，即k_a=-1，0，1；k_b为变流器b的工作状态值，取值同上。

图为n=2时输出电压的波形。显然，利用一个相对简单的两重的结构达到了7电平变流器的效果。分析表明，对于M重化的逆变器，当n=1，输出线电压电平数N_s=2M+1；当n=2，输出线电压电平数N_s=2^（M+1）-1；当n=3，输出线电压电平数N_s=3^M。

实际上，图6-22a电路可以简化为图6-22b，可以看出，后者比前者少用了两个开关器件，推而广之，对于一个M重变流器，简化回路可以省掉2（M-1）个开关器件。

上述结构通过简单的变换可以生成若干种新的形式的多电平变流器。由于工作原理相似，另外主要可以应用在传动系统之中，本文就不再加以讨论。

（4）多脉冲调制 在变流器中，如何实现降低谐波含量和控制输出电压是控制器设计的焦点。早期，FACTS用于大功率变流器中，为了降低功耗，多采用多重化加单脉冲宽度调制的方法，从结构上满足上述要求，但其后出现的变流器中，却几乎都采用了对线电压进行多脉冲调制的方法，尽管由于设计目的和控制方法不同，所达到的效果不尽相同，但其中很重要的一个原因是由于新方案多采用了180°导电型的三相桥电压源变流器作为基本模块。

三相桥变流器输出的线电压波形如图6-23所示，由于输出电压需满足三相对称和正负半周对称的要求，所以线电压的脉宽被固定为120°，如果没有其他控制手段，其输出交流电压的基频分量的有效值被直流中间电压所唯一确定。在采用储能电容来提供中间直流支撑时，调节无功输出的同时，电容上的电压将随之波动，即只能采用脉冲幅度调制，这是不希望的。再加上其谐波含量固定为18%左右，也是不希望的，所以为了达到调节的目的，唯一的方法是在基本的方波中实现脉宽调制。

图6-23 三相桥三脉冲电压波形图

上述线电压U_ab波形可以看作是由如图6-24所示，一个脉宽为120°的方波信号和两个与其幅度相同但脉宽为2θ的方波组合而成，在基频相位相同的情况下，由于基本方波信号的脉宽为120°，而两个脉宽为2θ的方波分布相对于基本方波存在30°的相移，所以合成后的信号的傅里叶展开式为

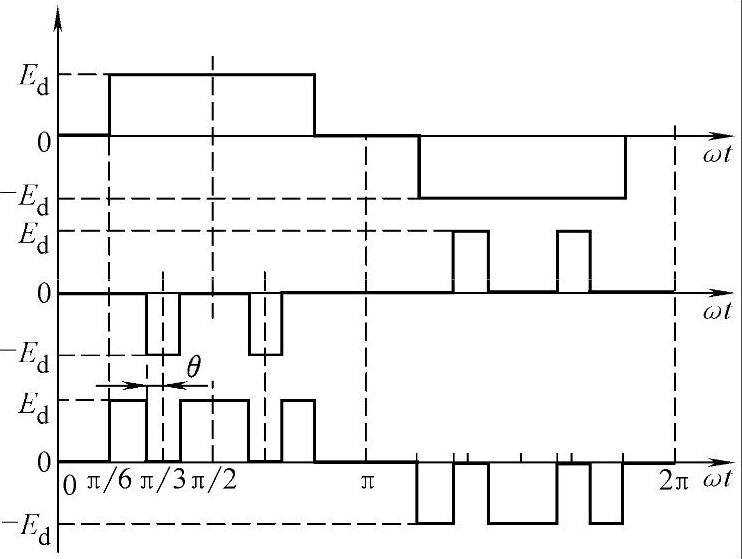
图6-24 矩形波合成

而当电容上的直流电压为E_d时，输出的基频电压有效值为

而输出电压中n次谐波电压的有效值为

所以基频电压的有效值和任一次谐波的有效值均依赖于开口的宽度，而由于上述三脉冲法只有开口宽度θ这一个可控变量，因此，只能完成控制基频电压或消除某次谐波这两个目标之一。如以消除某次谐波为控制目标，则根据上式），令n次谐波分量幅值为零的方法，即令下式为零：

比如常用的消除11次谐波代入，可以得到θ=19.09°，即开口宽度为38.18°；问题是，此时的脉冲宽度将降为120°-76°=44°，即电压利用率将大幅度下降，所以这种看似简单的方法在实际应用时需要慎重考虑。

如果采用开口的方式来维持直流电压恒定，比如在Toshiba的50MVA同步补偿器中所应用的那样，存在的问题同样是电压利用率低。比如，为了保证变流器交流侧输出电压不变，如没有开口时所需直流中间电压为13.5kV，而在允许最大开口为11°的条件下直流侧电压需要16.6kV（实际采用16.8kV），从而增加了器件耐压的要求。此外，图6-25中给出了以基频幅值U₁为参考，两重化三相变流器随着开口宽度变化各次谐波含量U₁的变化。显然，上述方式也导致输出谐波分量的变化。但由于它结构简单，可以有效地控制直流侧电压，提高装置的响应速度，所以在实际装置中仍得到一定的应用。

图6-25 不同开口宽度条件下输出线电压的谐波含量

以上对几种常用的阶梯波变流器进行了介绍，实际上每种方式均有其优点和存在的问题，并均得到广泛的应用，难以简单地断言哪种更好，应用中可以根据不同需要确定所选取的结构。