脉宽调制（PWM）技术简介与优化

脉宽调制技术是一个十分有效的谐波抑制方式，20世纪70年代以来，随着电力电子技术的发展，大量基于不同概念与性能的调制方式被开发出来^[2]。这里以单相逆变器为例作一简要的说明。图6-11a所示的单相逆变器的输入电压是直流电压U_dc，通过控制开关管适当的通断，可以在负荷两端得到如图6-11c所示的，一个周期内包括多个脉波的交流电压U_dc、0、-U_dc的三个电平电压波形U_p（t）。

而基于载波的PWM技术中^[3，4]，逆变器每个桥臂上开关的通断状态由调制信号u_c（希望的交流输出电压）与三角波u_Δ（载波信号）的比较结果确定，实际上，当u_c＞u_Δ时，开关VI₁、VI₄导通，开关VI₂、VI₃关断；当u_c＜u_Δ时，开关VI₁、VI₄关断，开关VI₂、VI₃导通。

作为一个特例，当调制信号是频率为f_c幅值为U_s的正弦波u_o=U_ssinω_st，而载波信号是频率为f_Δ幅值为U_Δ的三角波时，即正弦脉宽调制（SPWM）。在这种情况下，定义调制波电压与载波电压的幅值之比为调制比：m=U_s/U_c，而载波频率与调制波频率之比为载波比，定义为N=f_c/f_s。

图6-11 变流器输出SPWM电压及对应的正弦信号

a）单相逆变器原理图 b）、c）对应的正弦信号波形

根据采样控制理论的冲量等效原理，当冲量相等而形状不同的窄脉冲加在具有惯性的环节上时，其效果基本相同。这里，冲量指的是变量对时间的积分，也即窄脉冲的面积；而效果基本相同是指环节输出的波形基本相同，如把各输出波形用傅里叶变换分析，则它们的低频段特性非常接近，仅在高频段略有差异。根据上面理论可以用不同宽度的矩形波来代替正弦波，通过对矩形波的控制来模拟输出不同频率的正弦波，即利用脉宽调制的等面积计算方法利用矩形脉冲列来近似正弦波形。比如，将正弦波在半周期中N等分，并在每个等分区间通过积分，得到每个分段正弦波与横轴包围的面积，假定第i个区段的正弦波面积为S_i，可以由下式给出：

设矩形波的幅值等于直流侧电压U_dc，并使每段矩形波的面积等于相应段的正弦波的面积，则矩形波的脉宽可以由下式给出：

将每段矩形波置于等分区段中，即得到一组幅值相等而脉宽随正弦规律变化的脉宽调制波形。根据冲量相等效果相同的原理，PWM波形和正弦半波是等效的。对于正弦的负半周，也可以用同样的方法得到PWM波形。

以图6-11b所示为例，正负半周按等间隔方式划分为n个（图中为5个）子区间，每个区间的宽度为π/n=36°。每个区间具有一个幅值为±U_dc，宽度为θ_i（i=1，2，…，5）的双极性电压脉波，相邻两个脉冲中点之间的距离等于子区间宽度。

如果要求某一个时间段的脉宽为θ_i、幅值为U_dc的矩形脉冲电压面积等效于该时间段正弦电压u（t）=U_ssinω_st面积，根据式（6-15）得到第一区段的矩形脉冲宽度为

同理，可以得到其他四个区段的脉冲宽度分别为

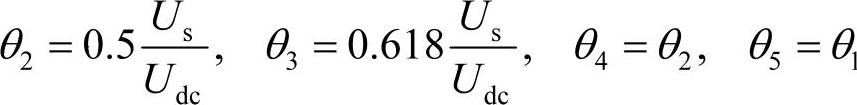
但是应当指出，上述原理是基于窄脉冲定义的，也就是要求PWM的采样频率要达到一个很高的水平，输出波形经过滤波后才能越接近理想的正弦波。但受到器件开关频率和开关损耗的限制，脉冲频率是有限的，也就是说，实际的脉冲不可能成为理想的窄脉冲，这就导致了逆变器的基频输出电压与由调制波决定的逆变器理想输出电压不可避免地存在差异。所以，这种基于面积相等原理的PWM方法的谐波消除效果较之基于谐波消除技术的其他PWM方法要差。

谐波消除技术中应用最广，也最为成熟的就是所谓SPWM，即正弦脉宽调制技术，其特点是一种调制波为正弦波、载波为三角波或锯齿波的脉宽调制法，它是1964年由A.Schonung和H.Stemmler把通信系统的调制技术应用到逆变技术中而产生的。直到1975年在英国Bristol大学的S.R.Bowes等的推动下，才使SPWM得到了广泛的应用和发展。这项技术的特点是原理简单、通用性强，控制和调节性能好，具有消除谐波、调节和稳定输出电压的多种作用，是一种比较好的波形改善法。SPWM包括两电平和三电平（前者也称双极性，即无论输出电压的正半周还是负半周均有正负脉冲电压；后者也称为单极性，即如图6-11所示，输出电压正半周只有正脉冲，负半周只有负脉冲）两种。而最常用的调制方法包括自然采样与规则采样两种。

所谓自然采样，就是以正弦波为调制波，等腰三角波为载波进行比较，在两个波形的自然交点时刻控制开关器件的通断。其优点是所得SPWM波形最接近正弦波，但由于三角波与正弦波交点有任意性，脉冲中心在一个周期内不等距，从而脉宽表达式是一个超越方程，计算烦琐，难以实时控制。以N=10为例，当起始点如图6-12所示在三角载波的负峰值，直流电压为2U_dc，参考正弦信号为U_s（t）=mU_dccos（ω_st+ϕ）时，两电平SPWM波的双重傅里叶函数表达式如式（6-16）^[4]所示：

图6-12 单相SPWM波形

a）余弦参考信号与三角波载波信号 b）输出电压 c）波形频谱

从上述表达式可以得到如下结论：

1）输出信号的第一项，即基频分量与调制比m成正比，并且与参考信号相位相同，上述性质说明，该调制方法为输出电压的基波频率、相位和幅值的控制提供了一个有效的工具。

2）输出信号的第二项是载波频率ω_c的函数，由于系数中包括sinjπ/2，载波频率的偶次谐波分量为0，而奇次谐波分量的幅值是贝塞耳函数J_o（mjπ/2）的函数，随着调制波m的增大而变小。

3）第三项为调制信号和其谐波的边带的函数。为了保证输出电压为奇谐波函数，N必须取奇数。

4）调制信号和载波信号频率的非整数倍频比所引起的可能的次谐波的影响通常完全可以忽略。

5）当调制比m高而载波N比低时，输出信号的失真最大，因为当载波比N低时，谐波成分增大，邻近频谱瓣之间会发生重叠，以致相邻边带的分量之间发生干扰的可能性增加。这种干扰通常仅在载波比小于11时才会产生显著的影响。

上述自然采样方法利用模拟器件可以十分容易实现。为简化讨论，同时不失一般性，假定调制信号和载波信号均以标幺值表示，此时如图6-13所示，调制信号U_s（t）=msinω_st。

(www.xing528.com)

图6-13 自然采样法

在利用数字计算机计算上述正弦调制信号和载频信号的交点时，两个交点由下述超越方程给出：

脉冲宽度为两个交点之间的差，即

这里，t₁=ω_s（kT_c+T₁），t₂=ω_s（kT_c+T₂），相应的面积为

当载波频率非常高时，由于采样周期很小，可以近似认为T₁≈T₂，式（6-19）可以改写为

S=T_cmsinω_st₁ （6-20）

而正弦调制信号在该时段的面积为

注意到，当载波比N＞7时，，即完全可以以T_c/2替代sin（T_c/2）而不至于引起大的误差。由此，当T_c→0，sinT_c/2→T_c/2，（k+1/2）T_c→ω_st₁，则上式可以记为

由式（6-22）与式（6-20），当载波频率足够大，即采样周期T_c很小时，二者的面积相等，换句话说自然采样是对正弦的一个很好近似。

自然采样法虽然对改善输出电压波形有利，但它有一个很大的缺点，即在线计算上述超越方程，需要用数值分析中的迭代方法求解，这就给实时控制带来很多困难，通常的做法是事先离线计算好交点，然后将数据放在计算机内存中，利用查表输出PWM波，但这将占用大量的计算机资源，规则采样的提出就为工程应用提供了一个有效的方法。

规则采样法是一种应用较广的工程实用方法，一般采用三角波作为载波。其原理就是用三角波对正弦波进行采样得到阶梯波，再以阶梯波与三角波的交点时刻控制开关器件的通断，从而实现SPWM法。当三角波只在其顶点（或底点）位置对正弦波进行采样时，由阶梯波与三角波的交点所确定的脉宽，在一个载波周期（即采样周期）内的位置是对称的，这种方法称为对称规则采样。当三角波既在其顶点又在底点时刻对正弦波进行采样时，由阶梯波与三角波的交点所确定的脉宽，在一个载波周期（此时为采样周期的两倍）内的位置一般并不对称，这种方法称为非对称规则采样。

规则采样法是对自然采样法的改进，其主要优点就是计算简单，便于在线实时运算，其中非对称规则采样法因阶数多而更接近正弦。其缺点是直流电压利用率较低，线性控制范围较小。下面以对称规则采样为例作一个说明。

自然采样法中，采样时刻取决于调制波与载波信号的交点，即调制过程，因此不是等间隔的，每个脉冲的中点并不和三角波的中点（即负峰值点）重合。规则采样法则采用等间隔采样的方式，如图6-14所示。如以三角波正峰值处作为调制波起点，此时采样点为t_n=nT_c，因此采样时刻与调制过程无关。实际实现过程是采样点t_i的调制信号m（t_i）被存储在工作频率为载波频率的采样保持器中，并且在下一个采样时刻t_i+1到来之前的时间段t_i～t_i+1中保持恒定，形成如图6-14所示的阶梯波。该阶梯波再与三角形载波相交，三角波两个正峰值之间为一个采样周期T_c，脉冲中点和三角波一周期的中点（即负峰点）重合，每个脉冲的中点都以相应的三角波中点为对称，使计算大为简化。

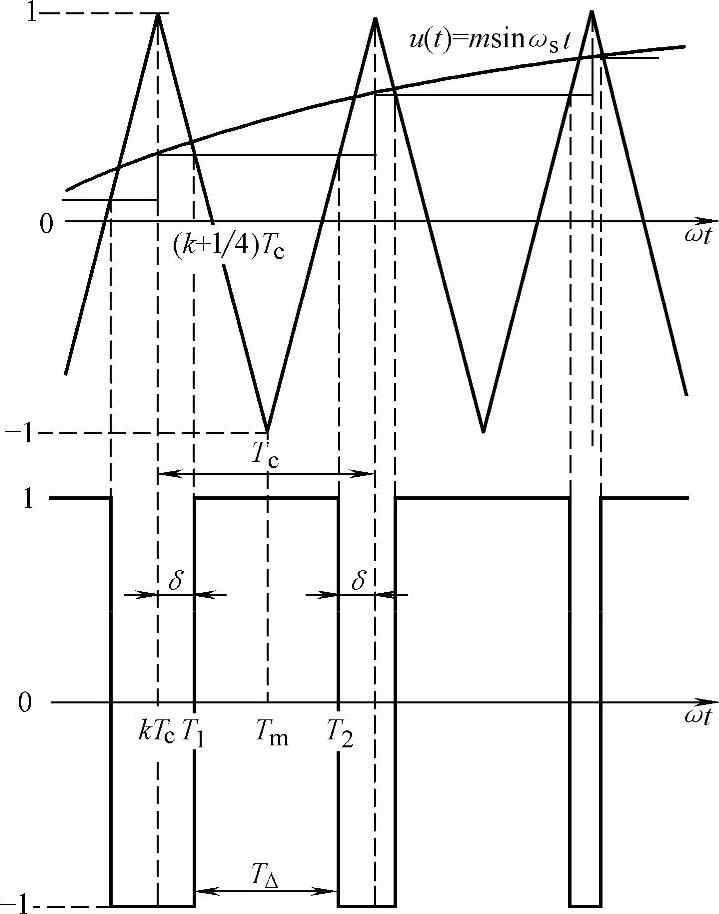
图6-14 对称规则采样法

图6-14中第一个采样点选取在采样周期的起点，即t₁=kT_c，则开关点可以由下式给出：

显然，上述两个开关点可以利用上式简单地计算得到，所以是一种便于计算机应用的PWM控制算法。而由于其等效面积为

S=mT_csinω_st₁ （6-24）

使上式与式（6-22）有相同的形式，故虽然规则采样在采样计算方面作了相当大的简化，仍然近似满足面积相等原理。

而在调制波信号仍是U_s（t）=mU_dccos（ω_st+ϕ）条件下，其输出电压相应的双傅里叶变换式变为

上式表明，规则采样较之自然采样便于实现的代价就是具有更为复杂的函数形式，特别是其贝塞尔函数的自变量不仅是调制比m的函数，还是载波比N的函数。由第一项可以看到，j=1所对应的输出信号的基频分量不再与调制比成正比，而是调制比m和载波比N的非线性函数。第一和第二两项还表明，输出信号中包括调制频率与载波频率所有分量，第三项则给出载波和其谐波的边带的幅值。显然，两种采样方法的频谱特性之间存在很大的差别。

对称规则采样的一个附加的优点是，由于脉冲函数对称轴处电流的失真为零，所以如果对该处对电流采样，得到的电流仅含电流的基频分量，故可以在开关周期中点采样而不需滤波器。

除了上述基于载波的两电平SPWM方法外，还有所谓三电平SPWM，以及所谓不含载波的调制方法，如特定谐波消除法以及空间电压矢量的PWM方法等，感兴趣的读者可以查阅相应文献，这里就不再赘述。