基于瞬时功率理论的补偿算法优化方案

上述瞬时功率理论为实时计算瞬时有功功率和无功功率提供了一个有力的工具，显然可以应用于冲击负荷的快速无功功率补偿之中。图5-23给出了一个瞬时无功功率补偿系统的基本框图，其中下标‘s’表示系统侧的量，‘L’表示负荷侧的量，而‘c’表示补偿器侧的量。

无功功率补偿的目的是由补偿装置提供负荷所需的无功功率，换句话说，瞬时无功功率补偿就是要消除流入系统侧的瞬时无功电流分量，这意味着如图5-23所示需要引入瞬时无功电流源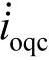、、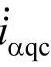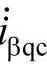，来对消负荷产生的瞬时无功电流，即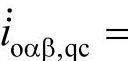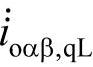，使得在任一时刻流入系统的无功电流相量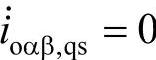，也即补偿后将没有瞬时无功电流在三相之间循环。为了实现上述控制，需要对电路中负荷的瞬时无功功率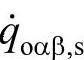和相应的负荷瞬时电流的无功分量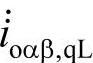，进行计算：

由此得到控制算法为^[4]

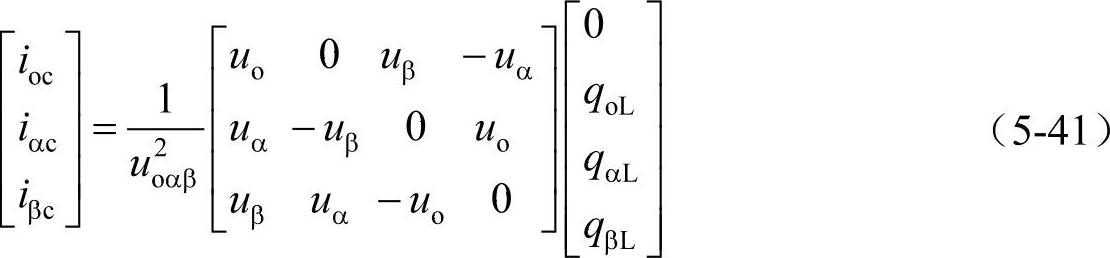
因为在补偿中不涉及有功功率的转换，即p=0，并且可能补偿器由不含储能元件的开关装置来实现。虽然在消除了瞬时无功电流后电源电流的方均根值会得到减小，但与零序电压成正比的零序电流仍然存在。

当零序电压为0时，上式可以改写为

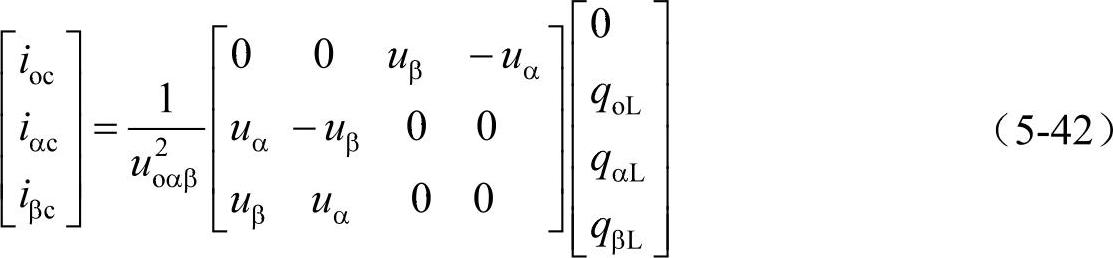
实际补偿系统中，由于往往采用三相三线制系统，所以系统中零序分量为零，此时上述方程可以缩写为赤木泰文最初采用的三相平衡系统的补偿模式。

此时，由方程式（5-32）不含零序分量的有功功率可以缩写为

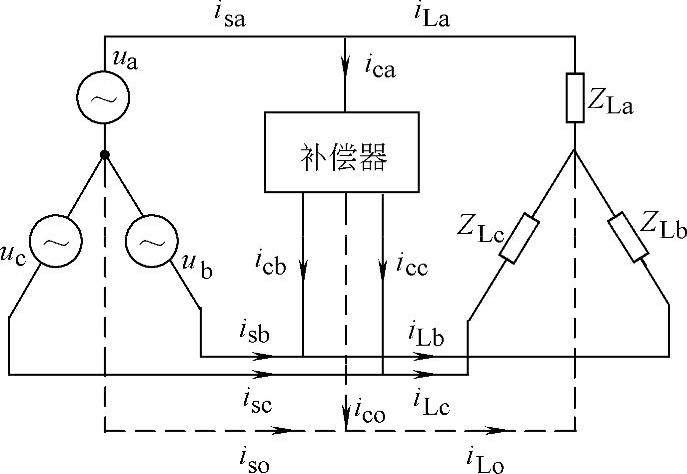
图5-23 三相四线制系统原理图

同理，不含零序分量的方程式（5-33）被缩写为

两者的组合就给出赤木泰文最早定义的瞬时功率方程

在赤木泰文的定义中，p是瞬时实功率，定义为同相电压与电流的积之代数和。换句话说，瞬时实功率为电流矢量与电压矢量的标量积；显然，瞬时实功率为含有能量的实体，是在αβ平面存在的实际物理量，如图5-24所示。而q被命名为所谓的瞬时虚功率，它由相互正交的轴上的电压和电流的乘积来定义，并且用来描述在不同相之间循环的瞬时功率。作为电流矢量与电压矢量的矢量积，显然，q是与αβ平面垂直的相量，即不含能量的虚的物理量。进一步的分析表明，实际上由传统功率理论，各相瞬时功率有功分量和无功分量得到的瞬时有功功率和瞬时无功功率的概念和赤木泰文定义的瞬时实功率和虚功率的概念是一致的^[8]，所以在以下的讨论中，除特殊注明外，均以瞬时有功功率和瞬时无功功率来定义。

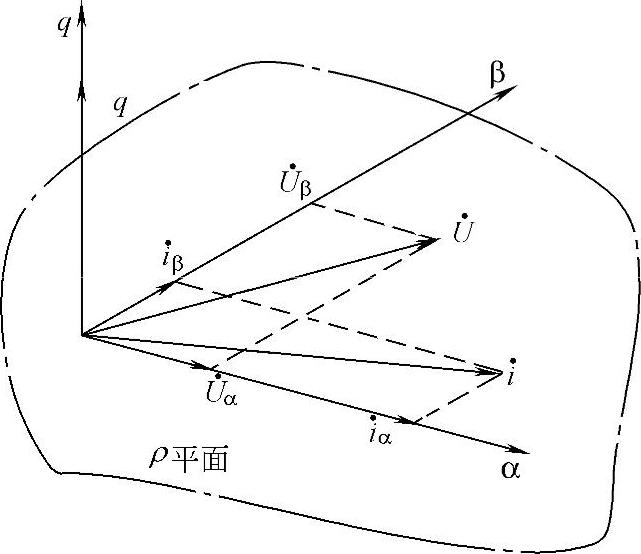
图5-24 瞬时功率相量图

在上述方程等式两边左乘系数阵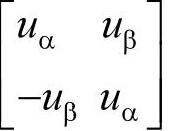的逆，得到相应的根据瞬时有功功率和瞬时无功功率分解的电流相量：

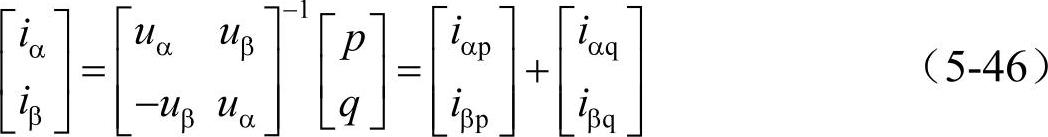
式中，i_αp是α轴上的瞬时有功电流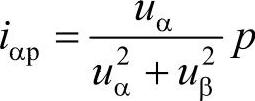，；i_αq是α轴上的瞬时无功电流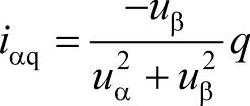，；i_βp是β轴上的瞬时有功电流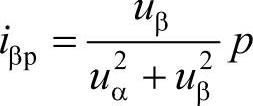，；i_βq是β轴上的瞬时无功电流，。

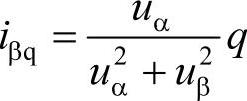由此，瞬时功率可以表示为

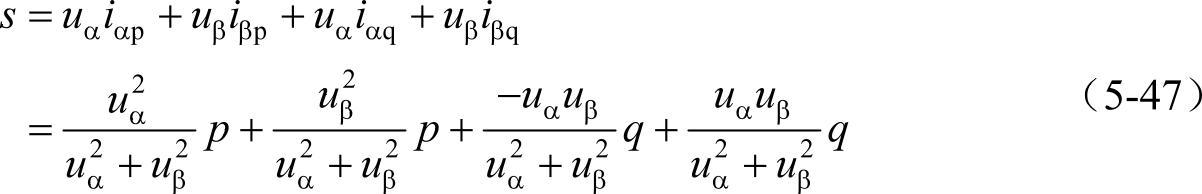
式中，第一和第二两项分别为在α、β轴上的瞬时有功功率；而第三和第四两项则分别为α、β轴上的瞬时无功功率，并且两项的和为零。所以无功功率补偿的目的就是消除第三和第四两项，此时系统不论在稳态还是暂态的位移因子均将为零，即不存在无功功率交换。为了实现上述目的，则相应的控制策略为

(www.xing528.com)

假定三相电压为对称正弦波形，而电流为任意的周期波形，此时瞬时有功和无功功率可以由下式给出：

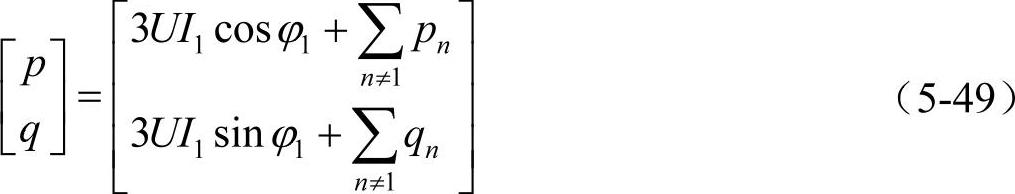
等式右边第一项为直流分量，其中包括正序电压和基频电流的幅值和相位的信息，代表瞬时基频功率。第二项是由于系统不平衡和谐波引起的交流分量。由此，可以将瞬时功率进一步划分为相应的直流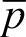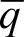分量、和交流分量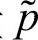、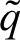，从而将两轴的瞬时电流记为

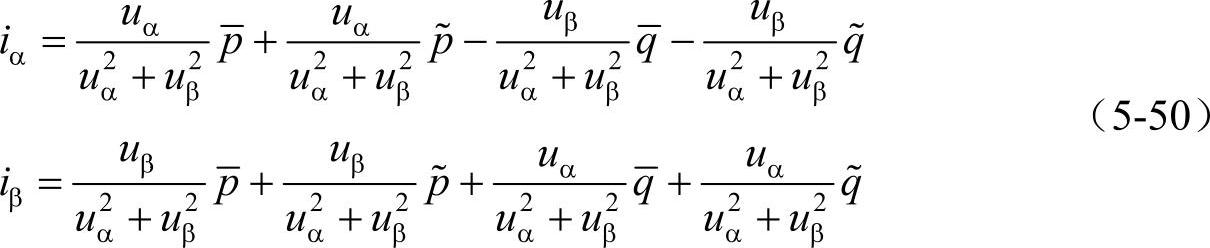
式中，等式右边第一项为基波有功电流的瞬时值；第三项为基波无功电流的瞬时值；第二项为谐波有功电流的瞬时值；第四项为谐波无功电流的瞬时值。波浪线～表示交流分量，直线-表示直流分量。注意到在正序同步坐标系上负序分量的频率为两倍的系统频率，所以也属于交流分量。实际上，同步坐标系上各变量的意义见表5-2。

表5-2 同步坐标系上变量的物理意义

而从补偿的角度对式（5-39）进行分析，可以看到如果将第三、四项表示的谐波电流作为补偿对象，即补偿电流为

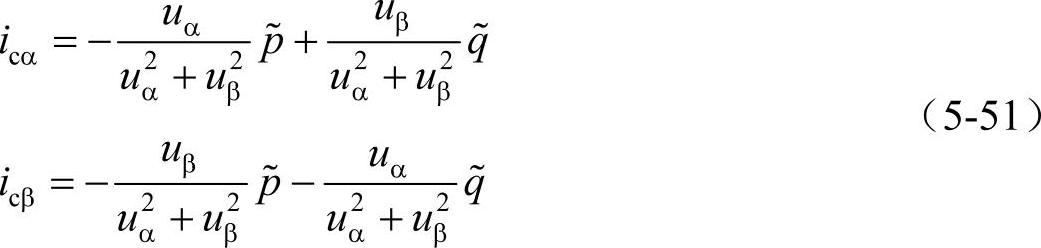
相应的电源电流为

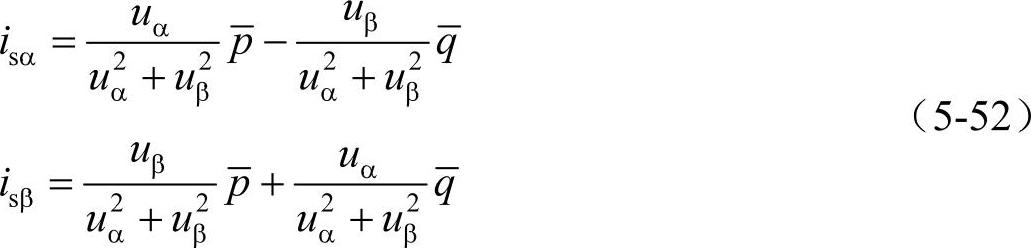
由于u²_α+u²_β为电压矢量的二次方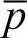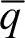；、为常量，故电源提供的电流的频率仅与电源电压有关，即仅含基频成分，所有的谐波成分均被抵消掉了，也就是说系统起了谐波滤波器的作用。

如果进一步将基波无功电流成分也包含在补偿对象之中，则由电源提供的电流将表示为

即仅含正序基频有功功率分量，显然对于电力系统而言这是最理想的。

从原则来讲，只要开关频率足够高，就可以在系统中产生所希望的任意波形的电流，从而制出理想的电能补偿器，以完成上述任务。但是在实际应用中，一方面，由于电力电子器件的开关频率较低，而限制了大功率的电力电子装置在谐波抑制中的应用。另一方面，由于开关器件的损耗随开关频率与开关电流的增加而增大，所以采用大功率高频变流器对所有有害成分进行补偿从经济上是不合理的。因此，目前这种理想的补偿装置的应用受到局限，实际中采用的往往是以某种特定对象为目的的补偿装置，根据补偿对象不同，补偿器的功用见表5-3。

表5-3 电能补偿器在电力系统中的应用

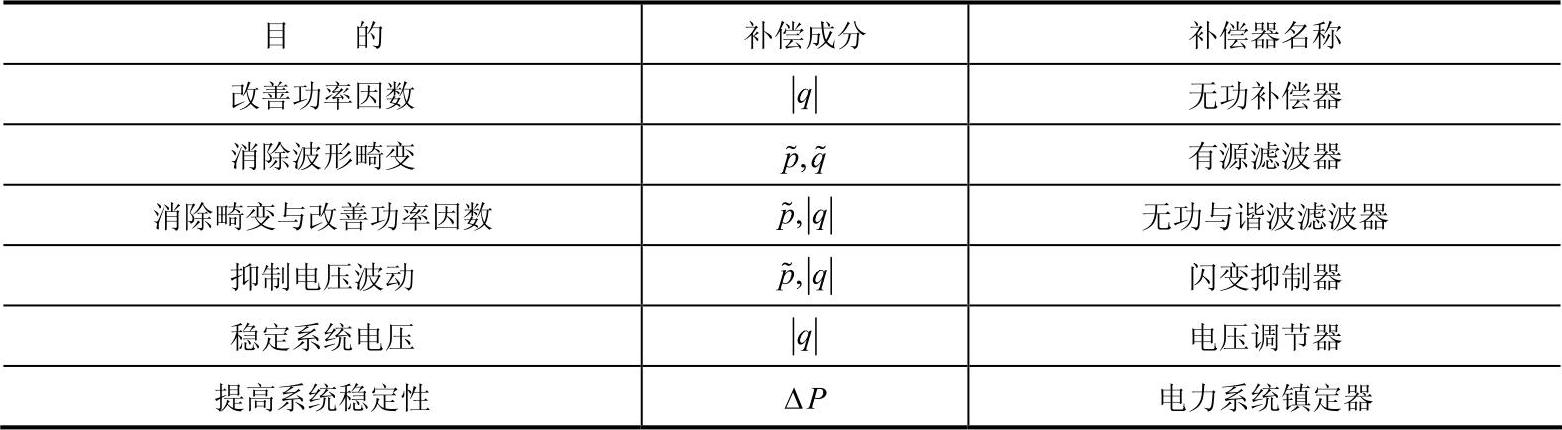
由此可以看到，所有上述补偿器均基于同样的控制机理。所以广义的电能补偿器可定义为“将系统中所含有害电流（谐波电流、无功电流及负序电流）检出，产生与其相反的补偿电流，以抵消的母线中有害电流电力电子变换装置产生”。

为了说明常规功率理论和瞬时功率理论之间的关系，以一个三相平衡系统加以说明。如前所述，在静止α-β-o坐标系中，电流和电压可以表示为

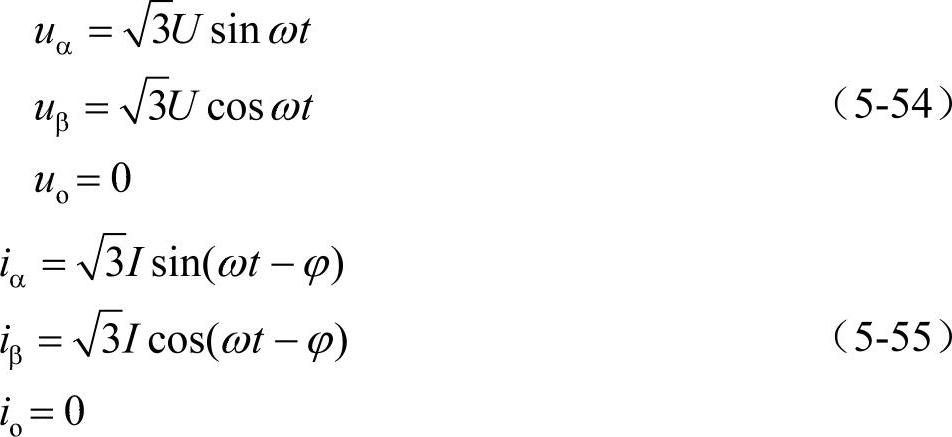
相应地，有功功率和无功功率均为常量，并可以表示为

p=3UIcosϕ

q=3UIsinϕ （5-56）

与方程式（5-28）、式（5-29）给出的结果完全相同，这说明在系统三相电压和电流对称，并且都只包含基波分量时，此时两个理论体系中，瞬时实功率p和传统的有功功率的定义相一致。而瞬时虚功率q的量值也与传统的无功功率相等，但作为瞬时虚功率的q与传统无功功率的物理意义是完全不同的，这一点读者必须十分清楚。此时瞬时功率理论中的瞬时实功率与瞬时虚功率的直流分量分别对应三相交流中的基频有功分量和无功分量；而交流分量则与三相电流中的谐波分量（包括负序分量）对应。