关于以正弦电压为激励的线性负荷电路的有功功率和无功功率的理论早已为人们所熟知并获得了广泛应用。但是随着非线性和时变负荷，如电力电子装置的应用日益广泛，使得深入理解瞬时无功功率和谐波功率的本质对于现代电力系统的成功运行变得越来越重要。近年来，许多研究人员试图在原有基于稳态平均概念之上的有功功率、无功功率、有功和无功电流、功率因数等基本概念进行重新定义，以对不平衡及失真条件下的电力系统参数进行描述。但是，只有赤木泰文提出的瞬时功率理论（Instantaneous Power）[2，3]才真正为上述问题的解决奠定了坚实的基础，并且在许多FACTS装置中得到了成功的应用。
为了更好地理解瞬时功率的概念，首先对基于时间平均概念，并且建立在稳态线性系统基础上的传统功率理论进行简要的说明。
根据定义，在任何情况下，瞬时功率是瞬时电势差和瞬时电流的乘积。
1.正弦电压激励的单相线性电路
对于线性电路而言，正弦电压激励和所产生的电流仍是正弦，并可分别记为
式中，ϕ为电压和电流之间的夹角；U、I为系统电压和电流的有效值。由此，瞬时功率可以记为
s（t）=u（t）i（t）=UIcosϕ-UIcos（2ωt-ϕ） （5-21）
如果以电压相量u（t）作为参考，将电流i（t）分解为与电压同相位的分量Icosϕ和与其正交的分量Isinϕ，上式可以改写为
s（t）=UIcosϕ（1-cos2ωt）-UIsinϕsin2ωt （5-22）
两项均包含一个以电网频率两倍频率变化的正弦变量，该量在一个周期中平均值为零。等式右边第一项为直流量，即其值始终大于零，定义有功功率为电压与相应电流有功分量乘积在一周期内的平均值，即
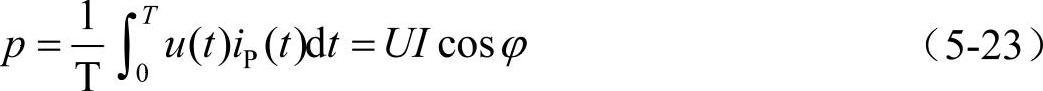
它代表不可逆的能量消耗。第二项表示的是一个平均值为零的量，其中振荡能量的峰值，即电压与相应电流无功分量乘积在一周期内的最大值被称为无功功率，表示为
q=UIsinϕ （5-24）
上述能量仅用于建立系统中的电场和磁场，即被储存在储能元件中，并且通过与电路交换能量最终被送回电路。
2.正弦电压激励的三相线性电路
对于平衡的线性系统，瞬时电压和电流可以表示为
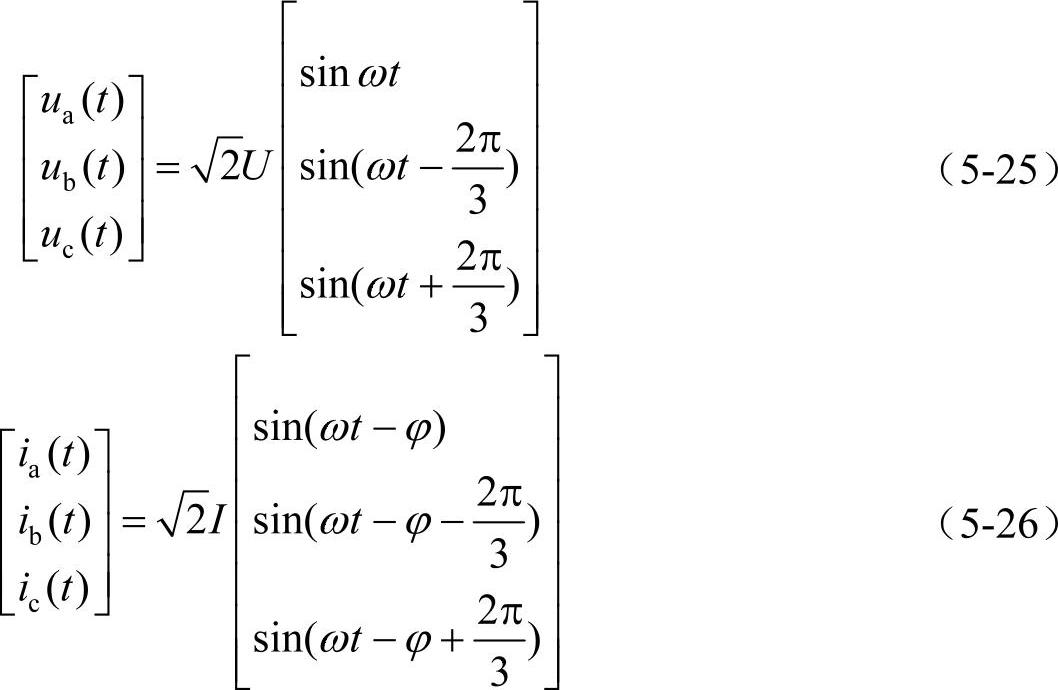
根据定义，电路的瞬时功率应当是三相瞬时功率之和
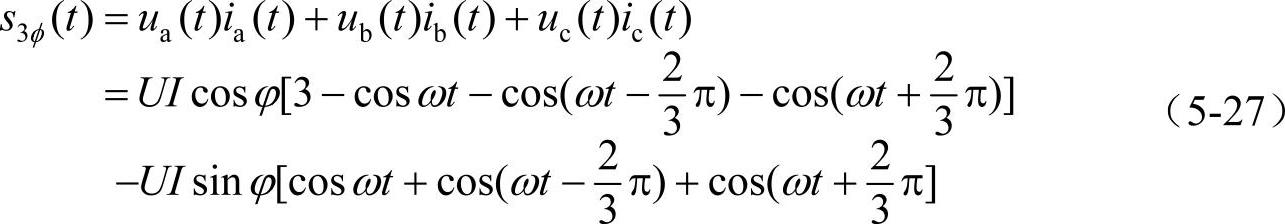
同理得到，由于三相平衡系统，上式第一项中的三个交变分量之和为0，所以平衡系统的三相瞬时有功功率为一个常量，即单相瞬时有功功率的三倍为
p3φ=3UIcosϕ （5-28）
同理，可以根据上述定义得到，三相系统的瞬时无功功率是每相瞬时无功功率之和，即
q3φ=3UIsinϕ （5-29）
上述理论的功率概念长期以来一直被成功地应用于电气工程领域，但是由于上述有效值（方均根值）的概念是基于时间平均的基础之上的，即是基于稳态交流系统的，它们只能用于表征以电源周期作为单位进行平均的系统参数变化的情况，这对于传统的发电机、电动机、电力系统的分析研究而言是足够了。而在新型的电力电子装置引入电力系统后，由于其动作周期远小于电源周期，以电源周期平均的方法进行描述，时间尺度显得太大，无法满足实际的需要了。比如采用有效值的概念，测量环节存在一个周期，即20ms的延时。这个延时对发电机励磁系统不会造成什么影响，而对响应时间为数毫秒到数十毫秒量级的FACTS控制器而言，该延时已经变得不可忽略，足以引起系统的振荡。
所以为了准确描述响应时间小于一个工频周期的FACTS装置的运行状态，需要有一个新的理论来对系统中无功功率、有功功率、电压、电流等概念进行描述。这就是赤木泰文于1983年提出的瞬时功率的理论，而为了将其扩展到包括三相四线制系统中，许多研究人员进行了大量的工作，下面以图5-21所示的模型为例，对其基本原理作一个简要的说明[2-7]。
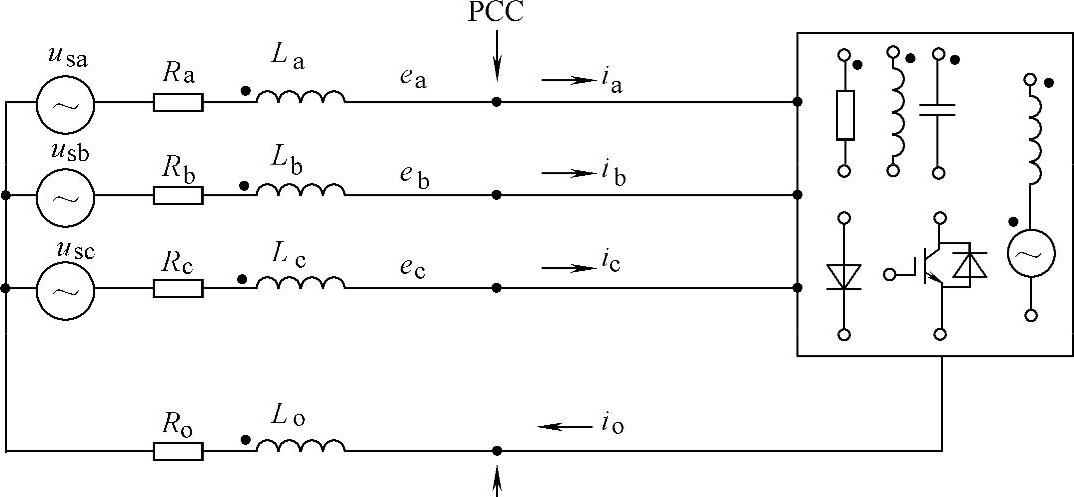
图5-21 三相四线制系统(www.xing528.com)
在如图5-22所示的静止α-β-o坐标系上一个三相四线系统可以记为
式中所有的变量均是瞬时值，并且包含所有的谐波分量。可以将输入电压和电流缩写为相量的形式：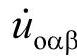
、
。
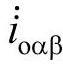据此，三相平衡电路的瞬时有功功率p在瞬时功率系统中被定义为电压和电流相量的标量积，即
式中，po为零序瞬时有功功率；pr=uαiα+uβiβ为按照赤木泰文瞬时功率理论定义的瞬时有功功率。这种变换的一个益处就是可以将有功功率的零序分量从有功功率中分离，便于进行讨论。而瞬时无功功率则被定义为电压和电流相量的矢量积，即
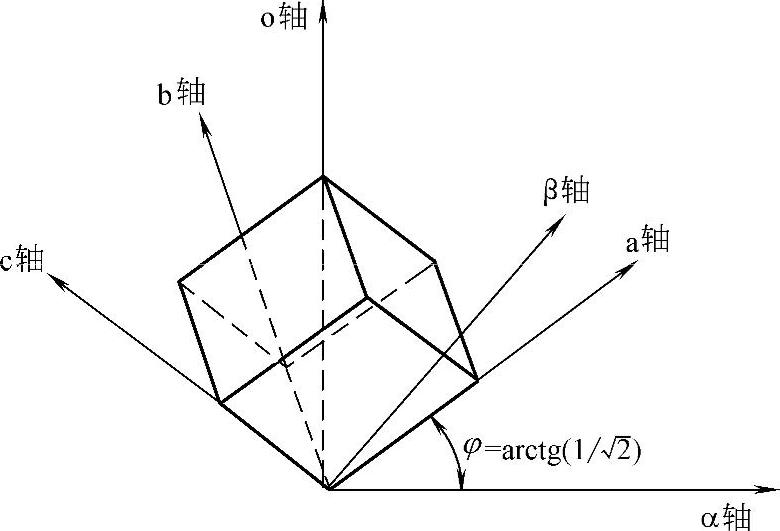
图5-22 abc和α-β-o坐标系之间的关系
对应的展开式为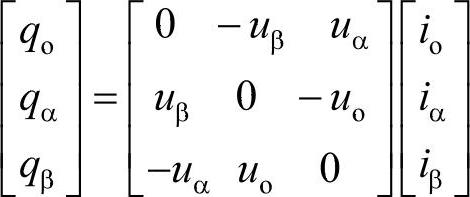
而与前相同，以其幅值定义瞬时无功功率，得到
根据上述定义，瞬时电流相量可以描述为
式中，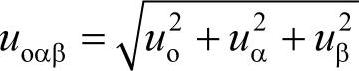
由此，瞬时功率电流相量可以被分解为两种瞬时电流分量，一个是瞬时有功电流相量，该相量是与有功功率p相关的电流分量之和，而且可以定义为
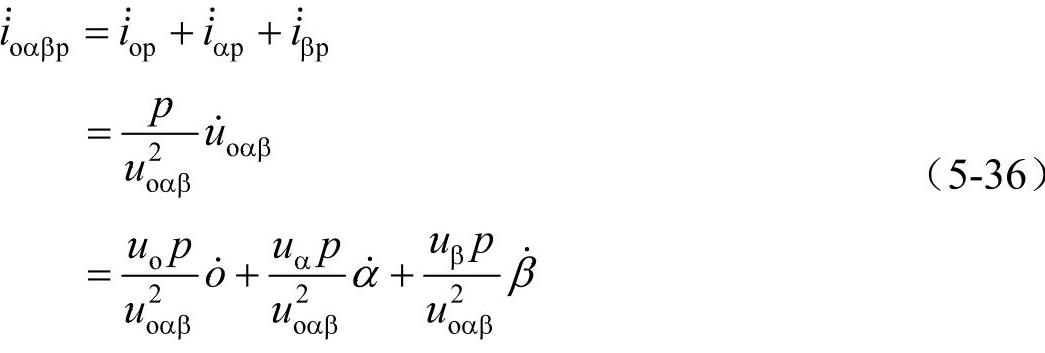
式中，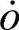
、
、
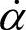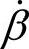是o、α、β三个轴的单位相量。
而瞬时无功电流相量，该相量是与系统交换的瞬时无功功率q相关的电流分量，而且与p类似，定义为
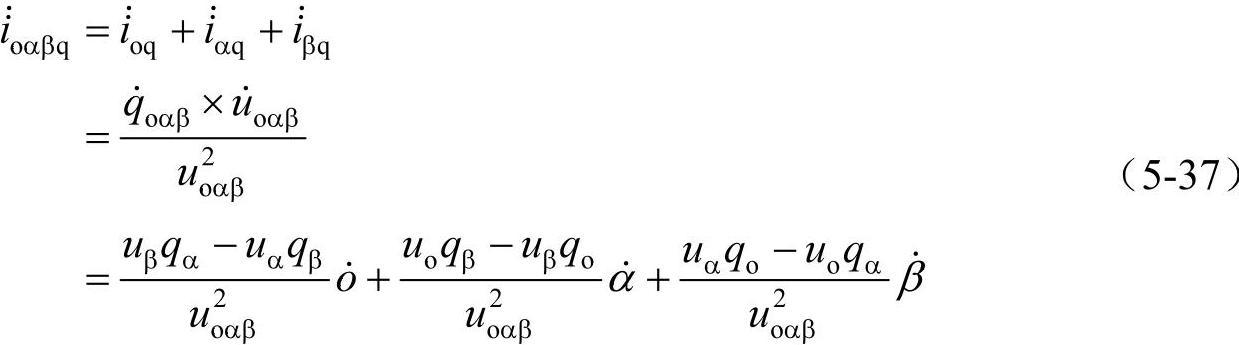
值得注意的是，上述所有这些量的计算均是实时的，即没有任何延时，所以它既可以用于稳态问题的计算，也可以用来计算暂态过程，这是这种新理论系统的主要优点。
如前所述，瞬时有功电流相量的各个分量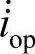
、
、
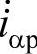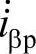，分别与瞬时电压相量相应的分量uo、uα、uβ平行，因此瞬时有功功率表达式（5-32）中，等式右边和式的各项是同一坐标轴上的电流和电压相量的乘积，即标量积。
p=po+pα+pβ=uoiop+uαiαp+uβiβp （5-38）
而瞬时无功功率表达式（5-33）中的瞬时无功电流相量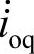
、
、
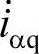，则与瞬时电压相量中相应的电压分量相正交，因此其矢量积，即瞬时无功功率为零。这说明瞬时无功功率实际上式在三相之间交换或循环，而并不像有功功率那样在线路中进行传输。因此，可以得到三相系统的瞬时有功功率和无功功率还存在下述关系：
从上述讨论可以知道，瞬时有功电流相量是瞬时有功功率传输的一个不可缺少的部分，而相应于瞬时无功功率相量的瞬时无功电流则在三相之间转换或循环。也即瞬时无功电流对于瞬时有功功率的传输没有起任何贡献，反而增加了由三相瞬时有功电流和瞬时无功电流的方均根值组成的瞬时电流的幅值，进而增加了线路损耗。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
