混合滤波器的设计与优化

混合滤波器的分类实际上有各种不同的方法，本节主要根据Singh^[12]的两级分类方法，按照构成滤波器的单元组件的类型（有源或无源）和数量，以及电路拓扑进行分类，并且将讨论局限在至少包括一个有源滤波器的范畴。

根据参考文献[12]，包括一个有源滤波器和一个无源滤波器的两单元混合滤波器具有8种主要拓扑，如图4-48所示。

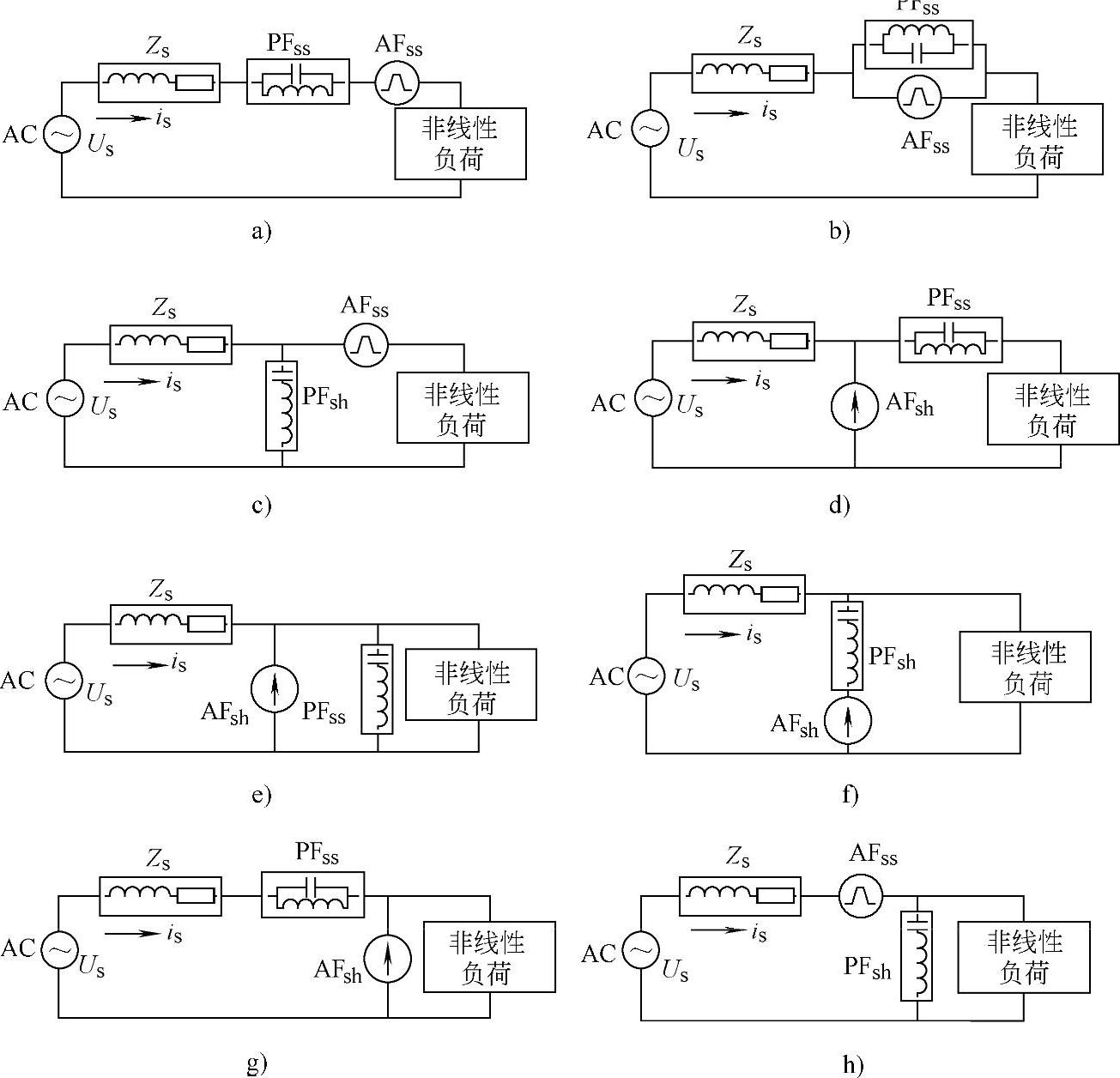
图4-48 两单元混合滤波器拓扑

a）串联连接的串联无源滤波器（PF_ss）和串联有源滤波器（AF_ss） b）并联连接的串联无源滤波器（PF_ss）和串联有源滤波器（AF_ss） c）并联无源滤波器（PF_sh）和串联有源滤波器（AF_ss） d）并联有源滤波器（AF_sh）和串联无源滤波器（PF_ss） e）并联连接的并联无源滤波器（PF_sh）和并联有源滤波器（AF_sh） f）串联连接的并联无源滤波器（PF_sh）和并联有源滤波器（AF_sh） g）串联无源滤波器（PF_ss）和并联有源滤波器（AF_sh） h）串联有源滤波器（AF_ss）和并联无源滤波器（PF_sh）

其中，基本组成单元为串联无源滤波器PF_ss（其中ss表示串联（Series））、串联有源滤波器AF_ss、并联无源滤波器PFsh[其中sh表示并联（Shunt）]和并联有源滤波器AF_sh4种。这里所说的无源滤波器可能是由若干个单调谐（通常是3个，两个低频的单调谐滤波器和1个高通滤波器）或多调谐滤波器的组合，而不仅仅意味着单个LC滤波器。而有源滤波器AF则可能是电流源CSI的，也可能是电压源VSI的；图中的电流源和电压源的符号只是表明，当有源滤波器串联在电路中时，其作用更近似一个可控电压源，通过向系统插入一个补偿电压来改善系统或负荷电压的畸变；而当其并联在主电路中时，其作用更接近一个电流源，通过向系统注入补偿电流来抵消有害的电流分量。

下面主要对两种主要类型的混合滤波器的功能加以适当的说明。

（1）并联连接的并联无源滤波器PF_sh和并联有源滤波器AF_sh此时系统等效电路如图4-49所示，图4-50则为一个电弧炉补偿的实例。以电流源i_L表示非线性负荷。

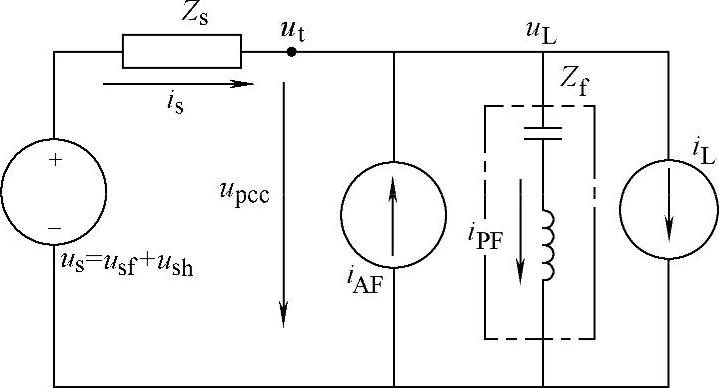
图4-49 并联连接AF_sh和PF_sh等效电路

假定将无源滤波器和负荷看作一个整体，而有源滤波器的目的就是补偿两者电流的谐波分量，则控制规律为

i_AFh=k（i_Lh+i_PFh） （4-74）

式中，k为有源滤波器的增益，或传递函数。而流经无源滤波器的电流为

据此，电流平衡方程可以表示为

i_sh=i_Lh+i_PFh-i_AF=（1-k）（i_Lh+i_PFh） （4-76）

由此可以得到电源电流的谐波分量为

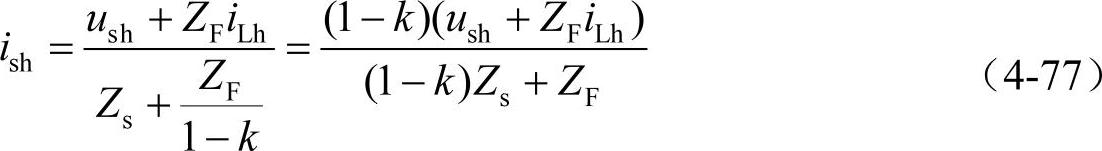
由上式可以看到，与前述混合滤波器的控制规律不同，此时仅当1-k→0时，电源电流的谐波分量才会趋近零，即实现对系统和负荷的谐波电流补偿。所以，对于刚性的系统不适于用这种并联补偿的方式来抑制谐波，而实际中也确实很少应用。

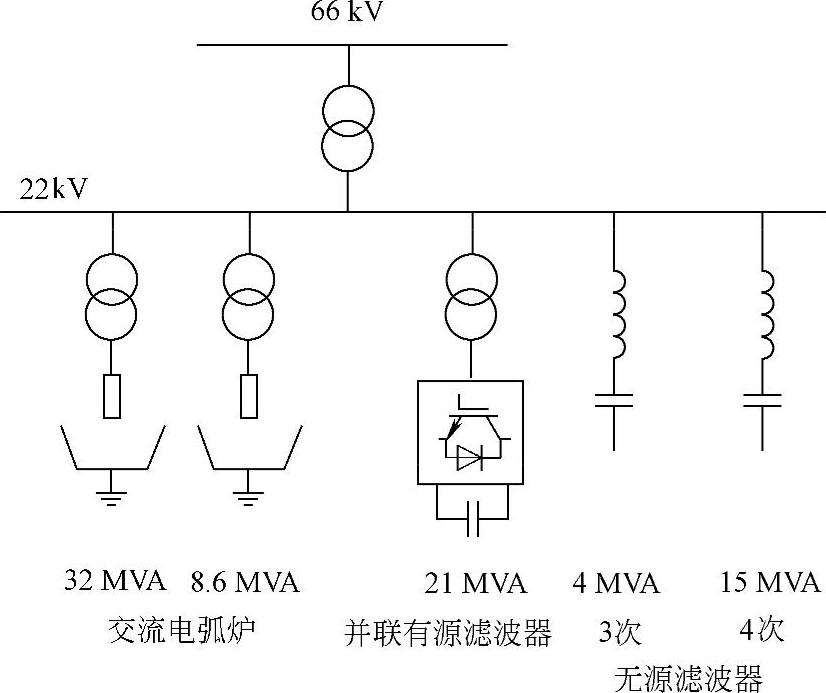
图4-50 用于电弧炉补偿的21MVA有源滤波器

此外由式（4-74）还可以看到，由于两个滤波器之间会发生相互作用，此时的有源滤波器的输出电流除了需要补偿负荷电流之外，还要对流入滤波器的其他谐波分量进行补偿，这会增大所需的有源滤波器的容量。

控制系统可以利用直流中间环节的电压控制达到幅值控制的目的，由于类似结构已经多次讨论，这里就不再赘述。

（2）串联连接的并联无源滤波器PF_sh和并联有源滤波器AF_sh一个典型的串联连接PF_sh和AF_sh的结构如图4-51a所示，相应的等效电路如图4-51b所示。

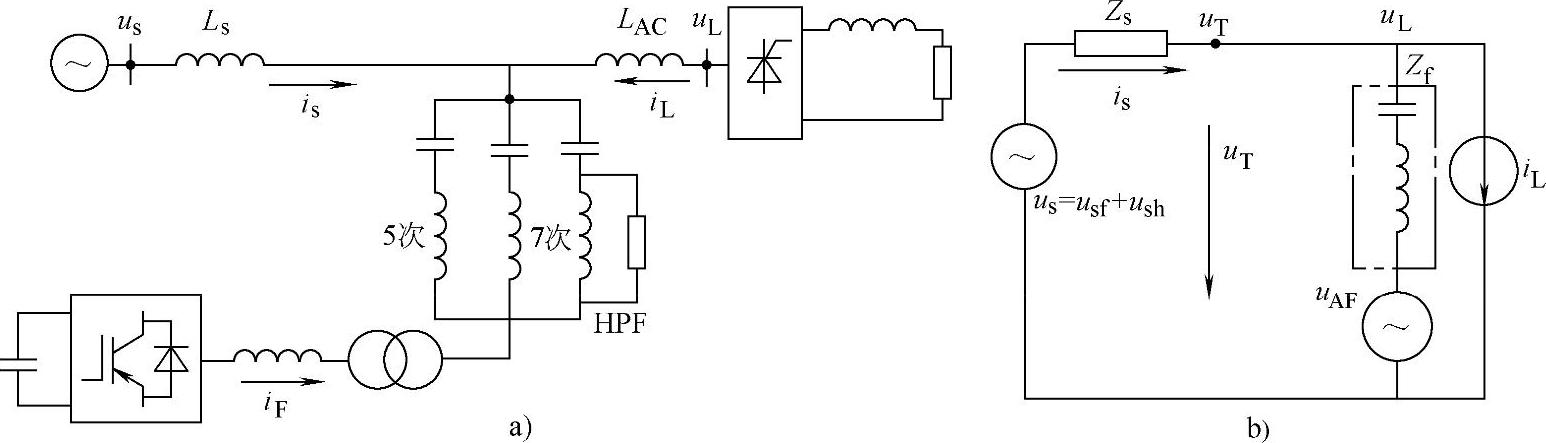
图4-51 串联连接的PF_sh和AF_sh的结构及等效电路

a）结构 b）等效电路(www.xing528.com)

假定将有源滤波器等效为一个受控电压源u_AF，控制规律为

u_AF=ki_sh （4-78）

可以得到电源电流的谐波分量i_sh为

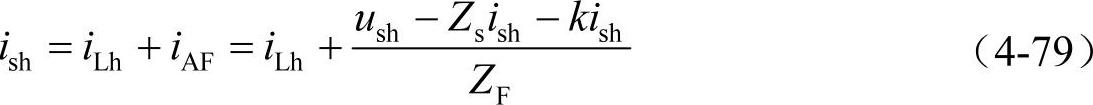
对上式求解，可以得到

显然，同样可以通过提高有源滤波器的增益k，使电源电流谐波分量为零。此时，可以得到接入点电压

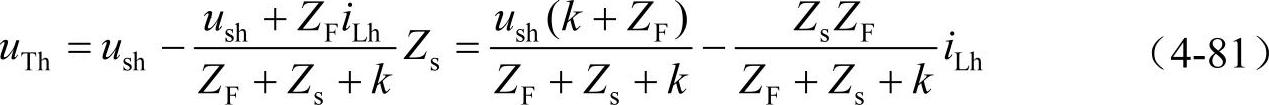
可见，采用上述滤波器结构，可以通过提高k使负荷谐波电流对接入点电压u_T的影响变得忽略不计，但对电源电压谐波分量u_sh造成的影响则几乎没有补偿作用。

图4-52给出了一个典型的并联滤波器构成的混合滤波器的原理图和控制系统框图，由于和前述图4-35的系统类似，这里就不加详细讨论。

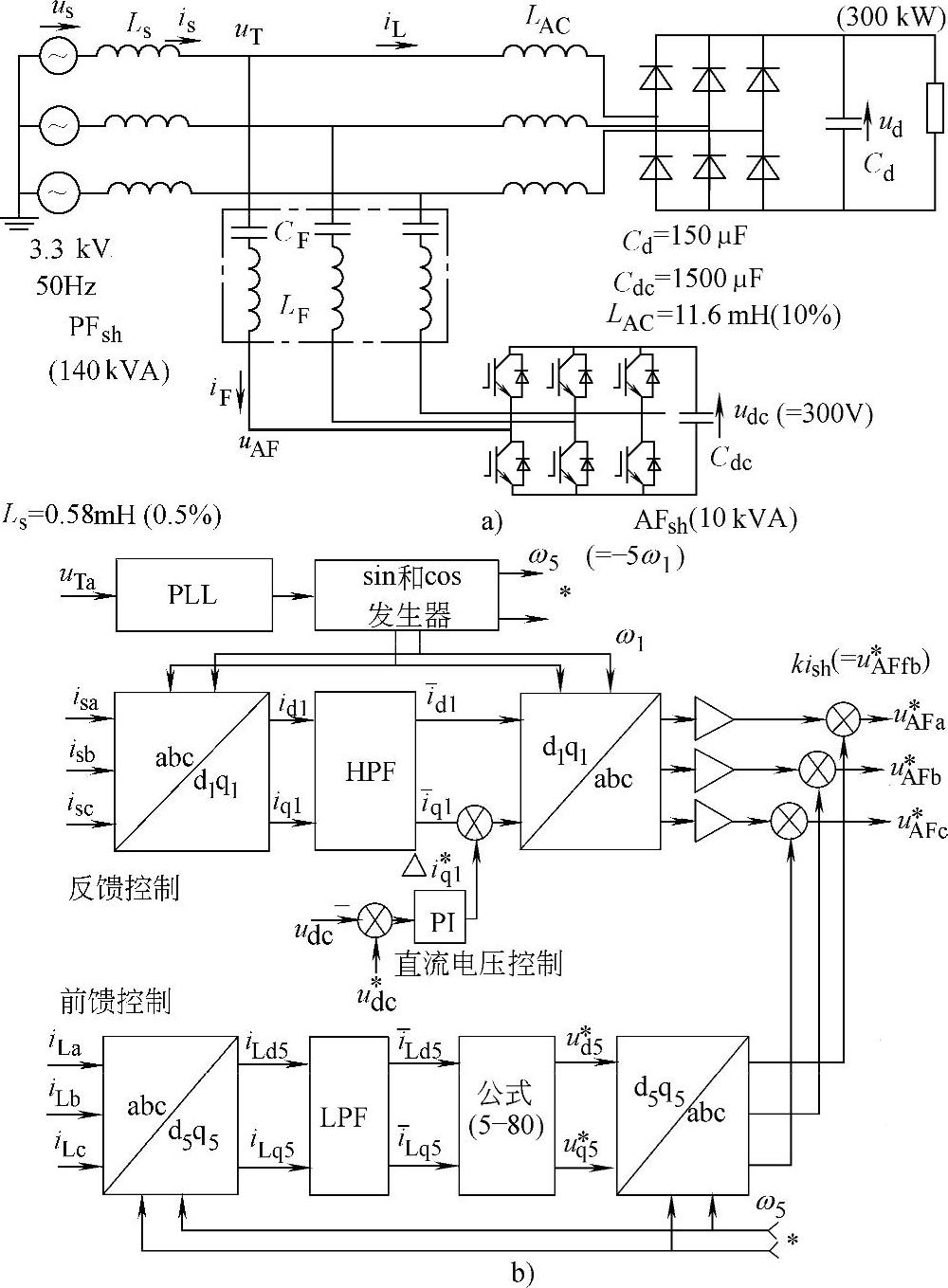
图4-52 串联连接的AF_sh和PF_sh原理图及控制系统框图

a）原理图 b）控制系统框图

图4-52b与图4-36的控制系统基本相同，由于前面已进行了详细的讨论，这里就不再赘述。其中变换方程为

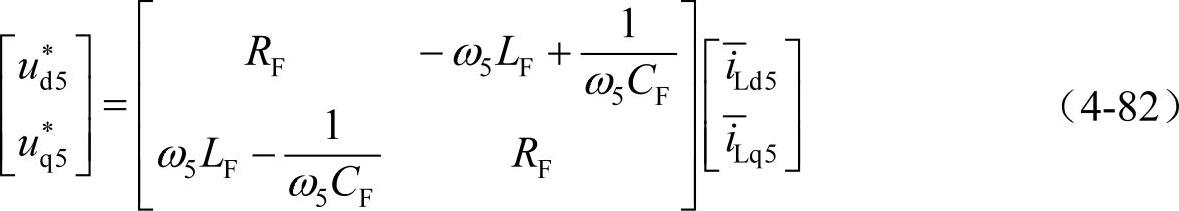
无源滤波器在系统中的作用是吸收由非线性负荷产生的谐波电流。实际应用中，无源滤波器通常均由5次、7次单调谐滤波器和一个高通滤波器组合而成。而为了消除有源滤波器开关频率的噪声，在常规的混合滤波器中所用的无源滤波器，通常还需附加的消除开关频率脉动的滤波器，如11、13次单调谐滤波器，来替代高通滤波器，但这通常造成滤波器的体积过于庞大。在参考文献[7]采用的结构中，仅采用一个7次单调谐滤波器，而以前馈的方式来消除5次谐波分量，从而大大减小了滤波器的体积。图4-53给出了混合滤波器的滤波特性，在7次谐波的邻域呈现低阻抗；当没有有源滤波器时，在200～340Hz范围内存在谐波放大现象；而当有源滤波器接入后，完全消除了谐波放大现象。这说明上述控制方法的有效性。

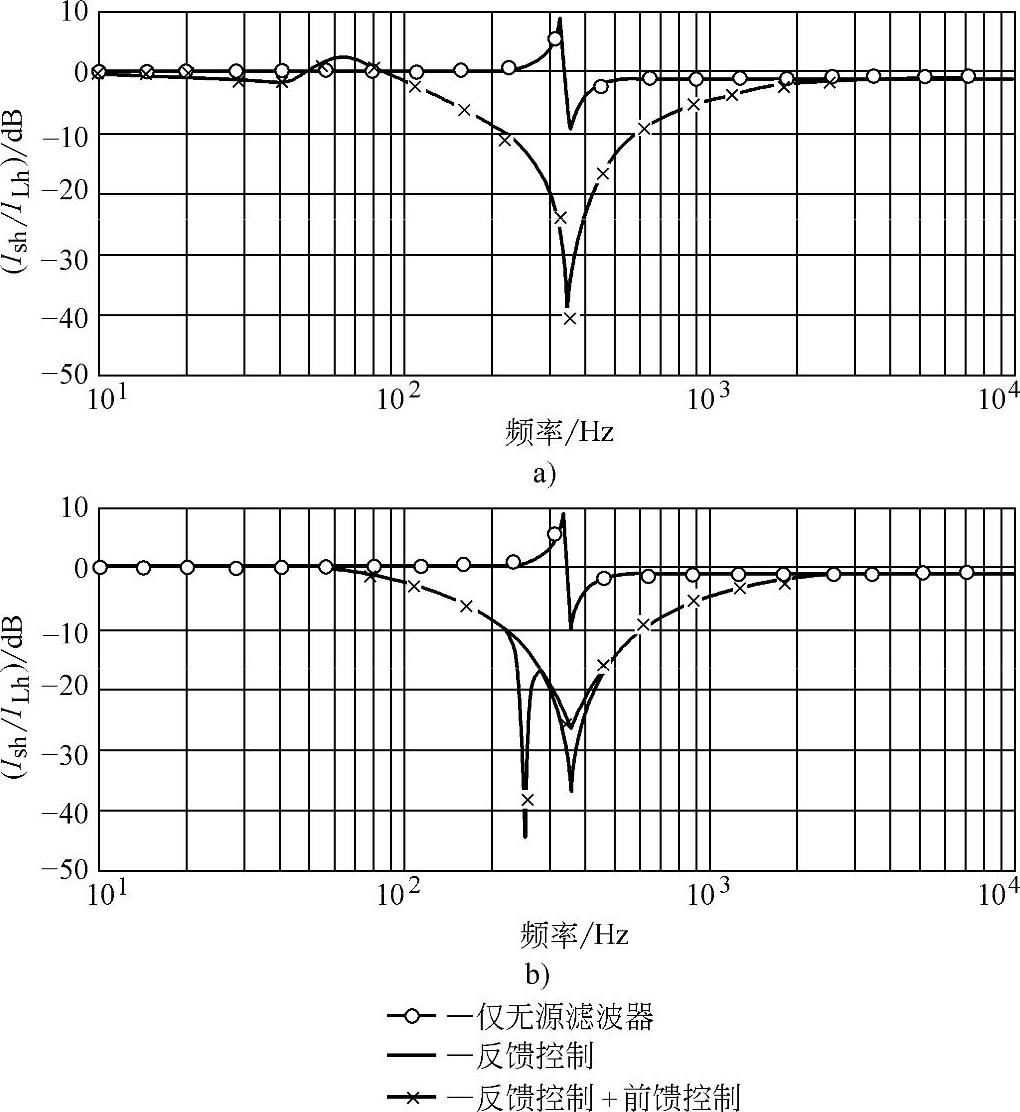
图4-53 混合滤波器的滤波特性（k=36Ω）

a）正序分量 b）负序分量

作者利用计算机仿真的方法对图4-52a所示的系统进行了计算，其结果如图4-54所示；随后由利用一个容量为0.16kVA的有源滤波器和相应的无源滤波器组合而成的实验室装置，对一台220V、5kW的二极管整流负荷进行了实验，实验结果如图4-55所示。

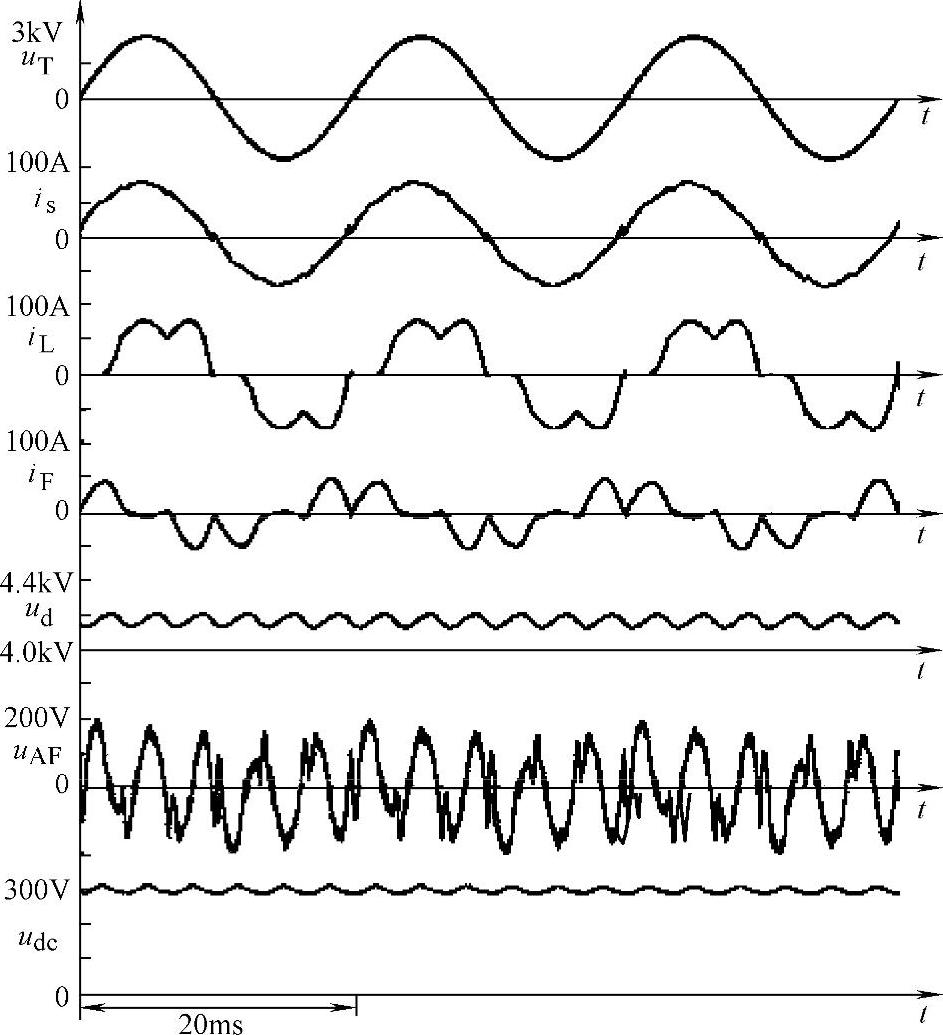
图4-54 3.3kV、300kW模型系统的仿真结果

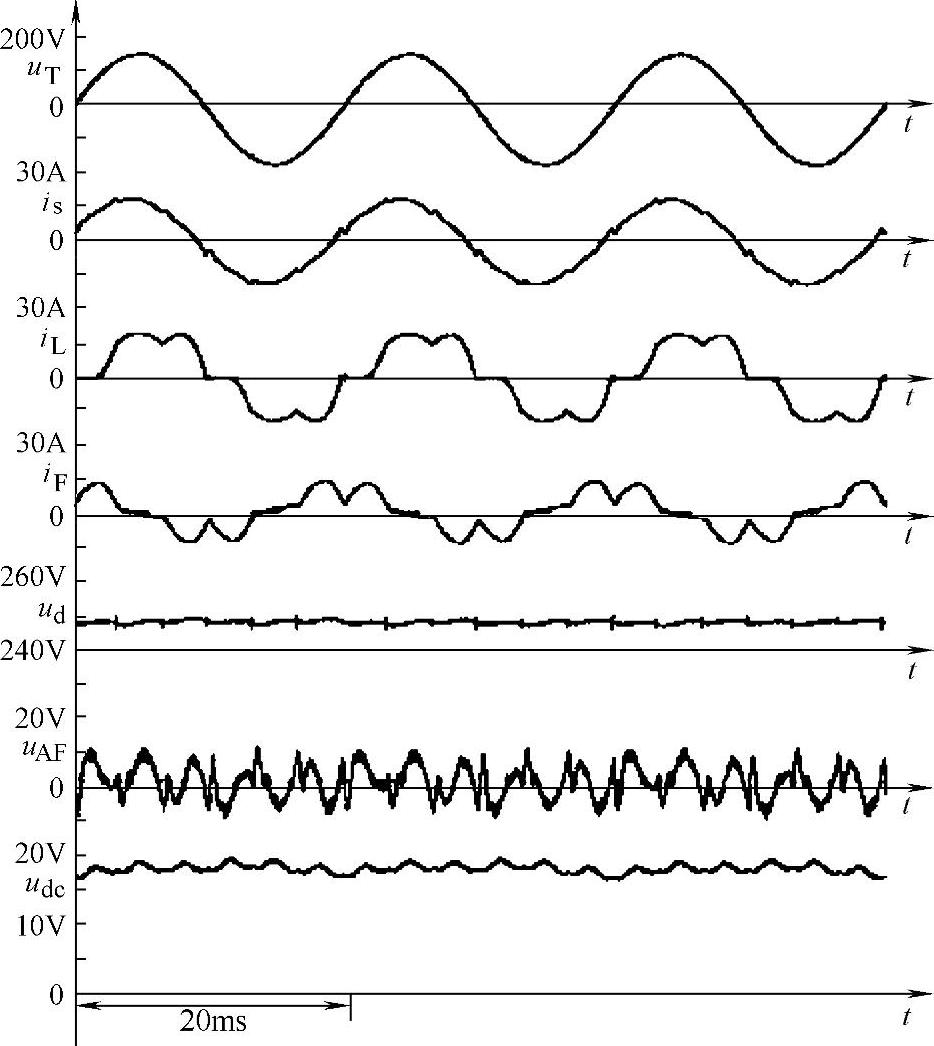
图4-55 200V、5kW整流器负荷的实验室补偿结果

仿真和实验的结果均表明，在采用单个无源滤波器的条件下，串联连接的混合滤波器可以有效地对非线性负荷进行补偿。而所提方案不需借助耦合变压器与供电线路连接，可以进一步缩小补偿器的体积。特别值得注意的是，上述串联结构可以使所需有源滤波器的容量较之常规的并联连接的有源滤波器大幅度减小。所有这些都证明了所提方案的优越性，为今后实用化提供了一个可行的方案。