如何设计纯有源滤波器？

现代有源滤波器作为一种广义的补偿装置，被赋予了一系列电能质量控制功能，这包括：谐波滤波、阻尼振荡、隔离和终止、无功补偿以校正功率因数和控制电压、负荷平衡、电压闪变抑制，以及上述功能的综合。电力电子器件和信号处理设备价格的降低，为开发和制造有源滤波器，并将其投放市场提供了动力。目前，有源滤波器以其比传统无源滤波器更小的体积、更好的性能和更灵活的应用得到了越来越广泛的关注。但作为有源滤波器的核心即逆变器而言，电压源和电流源逆变器均是可能的，但由于电压源逆变器的损耗、体积和噪声均较之对应的电流源逆变器要小，所以除了某些特殊场合，比如采用超导储能装置外，通常成为首选。而从结构上看，纯（pure，相对于混合而言）有源滤波器包括串联和并联两种结构形式，但就目前而言，并联滤波器由于其结构和功能上的优越性，受到更为广泛的应用。

1.有源滤波器的结构与性能

有源滤波器的功能是检测和补偿谐波源产生的谐波，而根据检测方法的不同通常将有源滤波器分为两类，即所谓反馈控制型的有源滤波器其特点是检测电网的谐波信号，然后产生补偿信号对其进行抑制；另一类则称为前馈控制型的有源滤波器，它的功能是检测谐波源的谐波信号，然后对其进行补偿。

图4-22给出了反馈控制型有源滤波器的等效电路。图中，Z_n为谐波源的谐波阻抗，Z_s为线路阻抗，u_s为电网电压。由于负荷均连接在线路上，故在讨论谐波污染问题时可以认为上述等效电路中u_s的基频分量为零，而线路阻抗Z_s上电压的谐波分量即看作是受电端电压的谐波分量。为了便于比较不同结构有源滤波器的性能，这里采用所谓有源滤波器对高频分量的“插入损耗”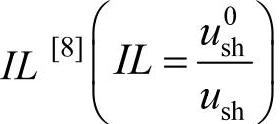，作为分析的依据。

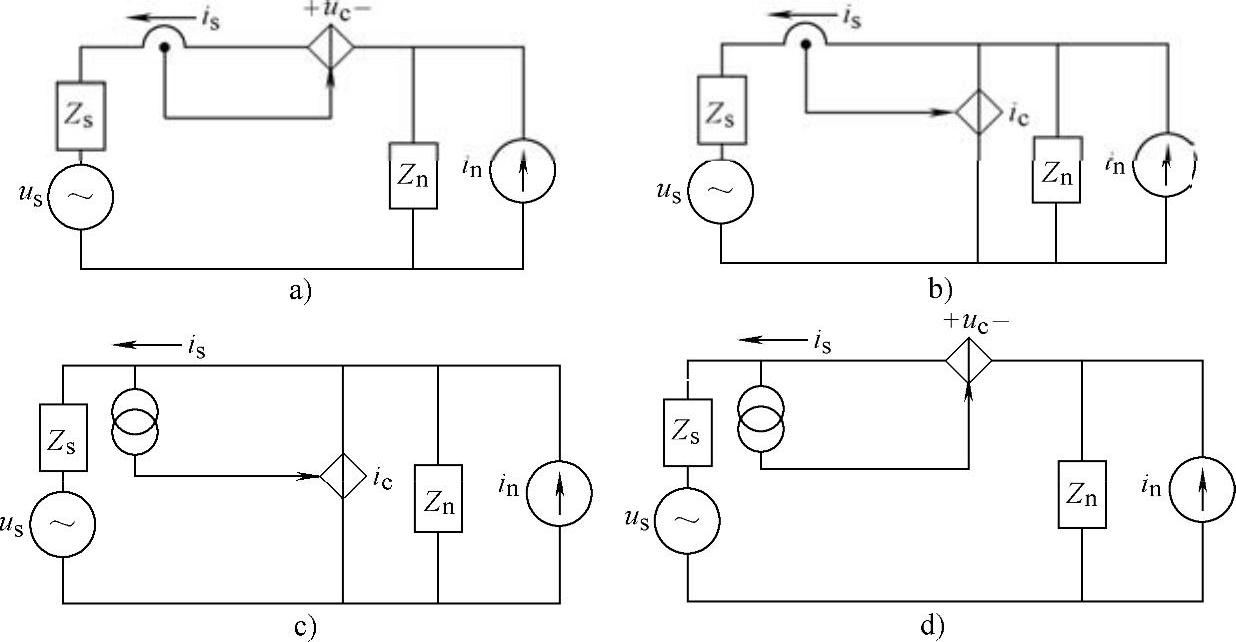
图4-22 反馈型有源滤波器等效电路

a）电流检测电压补偿（I型） b）电流检测电流补偿（Ⅱ型） c）电压检测电流补偿（Ⅲ型） d）电压检测电压补偿（Ⅳ型）

其中，u⁰_sh是没有任何滤波器时受电端的谐波电压，而u_sh是接入有源滤波器以后受电端的谐波电压。插入损耗IL表示接入有源滤波器前受电端的谐波电压分量与接入后受电端谐波电压的比值，所以IL越大，说明有源滤波器对谐波的抑制作用越大。而如果IL＜1.0，则意味着接入滤波器后谐波电压分量反而增大，即有源滤波器对谐波起了放大作用，这是我们所不希望并且要极力避免的。

对于Ⅰ型结构如图4-22a所示，串联在谐波源和负荷之间的有源滤波器应当具有很大的串联阻抗，以阻断谐波源谐波对负荷的影响，所以补偿器的增益应当尽可能大于系统的阻抗，注意到忽略电路中电源u_s时，滤波器接入前受电端电压为

由滤波器互阻抗u_c=-k₁i_s，得到滤波器接入后受电端电压为

故Ⅰ型滤波器的插入损耗为：

显然增益k₁越大，则插入损耗越大，或者说谐波分量的抑制效果越好。为了达到理想补偿效果要求k₁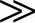Z_n+Z_s。

对于图4-22c所示的Ⅲ型结构而言，可以得到类似的结论，此时由于i_c=-k₃u_s，故

相应的插入损耗为

此时，只有当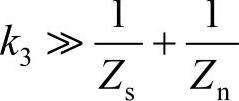，即有源滤波器的导纳远大于原系统的导纳时，才能得到理想到补偿效果。此时滤波器的作用和常规无源滤波器相似，为谐波电流提供一个低阻抗的通路，从而减少流入受电端的电流，达到降低施加于受电端到谐波电压的目的。从式（4-46）和（4-48）可以看到，这两种结构的插入损耗IL依赖于系统阻抗，为了提高补偿效果均要求滤波器的增益远大于原系统的总阻抗（或导纳）。由此，对于Ⅰ型而言，假如谐波源是电流型的，即阻抗Z_n→∞，则由于有源滤波器的增益是有限的，插入损耗趋近于1，也就是几乎对谐波没有抑制作用，或者说其补偿效率很低，所以不适于对电流型的谐波源，如负荷为大电感的整流器进行补偿。而对于Ⅲ型结构而言，如果谐波源是电压型的，即Z_n→0，或其导纳无穷大，则同样不能达到满意的补偿效果，即不适宜用于电压型非线性负荷的补偿。

研究表明，实际上只要有源滤波器的增益足够大，并且与谐波信号相位相同，即呈纯阻性，则完全可以在忽略系统参数的条件下，达到理想的补偿效果。

而对于Ⅱ、Ⅳ两类结构，其插入损耗与系统参数无关。以拓扑Ⅱ为例，由i_C=-k₂i_s得到

如果谐波源的内阻Z_n远大于线路阻抗Z_s，即Z_n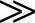Z_s，插入损耗IL为

IL₂≈1+k₂ （4-50）

即此类滤波器适于对具有无穷大阻抗的电流源性质的谐波源进行补偿，同时其插入损耗正比于有源滤波器的增益。而Ⅳ型滤波器在谐波源导纳远大于线路导纳Y_n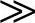Y_s，换句话说，在其内阻远小于线路阻抗，即Z_n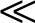Z_s时，具有类似特性

IL₄≈1+k₄ （4-51）

图4-23则表示前馈型有源滤波器的等效电路。图4-23a对应的拓扑Ⅴ型与拓扑Ⅱ型相比，除传感器的设置点外，高频等效电路完全相同。只是前馈型是检测谐波源的电流，而反馈型是检测受电端，即电源侧的电流。同样拓扑Ⅵ型和Ⅳ型具有类似的关系。而拓扑Ⅰ型（即电流检测电压补偿型）和Ⅲ型（即电压检测电流补偿型），两种涉及跨导的电路结构，则没有对应的前馈电路。

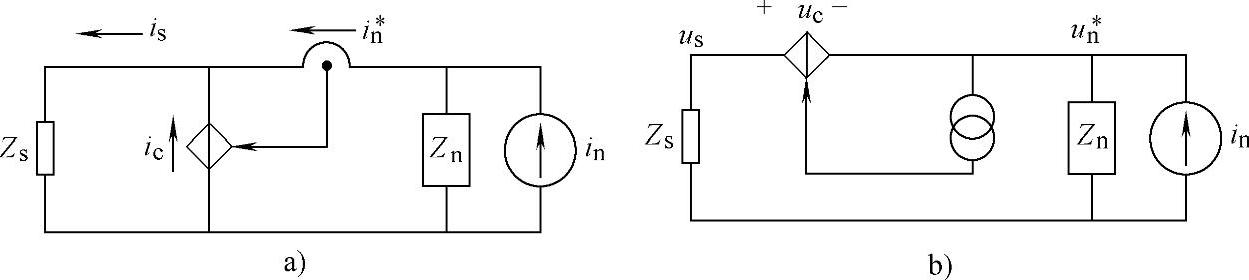
图4-23 前馈型有源滤波器等效电路

a）电流检测电流补偿型（Ⅴ型） b）电压检测电压补偿型（Ⅵ型）

由表4-13可以看出，当有源滤波器的增益为1时，前馈型有源滤波器具有无穷大的插入损耗，即可以完全消除谐波分量对受电端的影响。否则滤波器的补偿效果有限。对于Ⅴ型结构，如果谐波源接近于电流源，即如拓扑Ⅱ型时Z_nZs，

即插入损耗可以近似看作与系统阻抗Z_n、Z_s无关。

表4-13 有源滤波器的插入损耗和谐波改善率

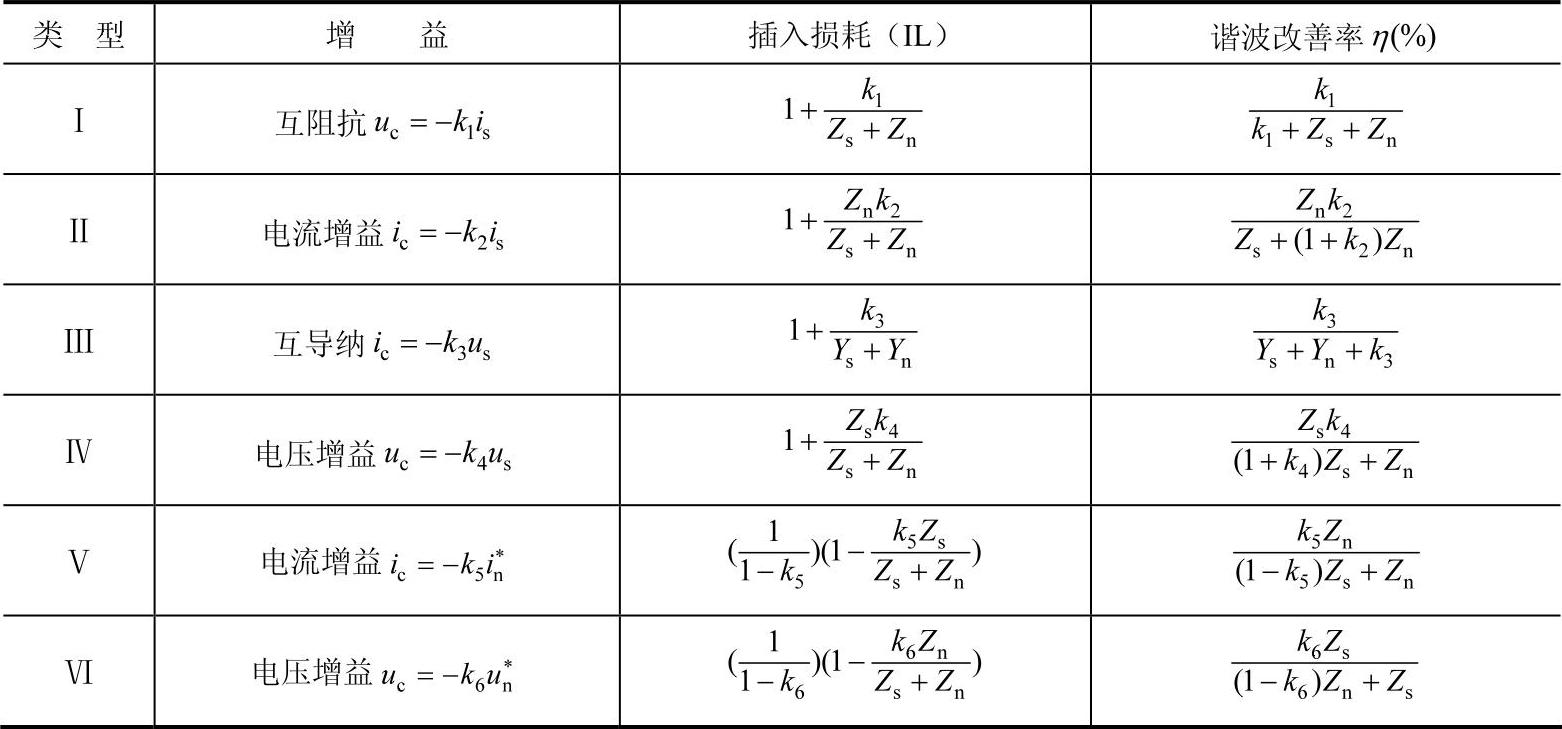
注：，。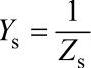

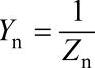对于Ⅵ型结构，如果谐波源接近电压源时，即如拓扑Ⅳ型时Z_n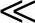Z_s，

综上所述，电压补偿型的装置，如Ⅰ、Ⅳ、Ⅵ型有源滤波器可以通过提高线路的谐波阻抗，来限制流入受电端的谐波电流；理想条件下，电压补偿型的有源滤波器可以对谐波电流起到完全补偿或阻断作用，此时实际上流经滤波器本身的谐波电流也为零。而电流补偿型有源滤波器，如Ⅱ、Ⅲ、Ⅴ型的功能是为谐波源发射的谐波电流提供一个低阻抗的通路，或者说通过使谐波源产生的谐波电流最大限度地流经电流型有源滤波器，来减少流入受电端的谐波电流。实际上此类有源滤波器并不会减少在系统中循环的谐波电流，只是重新安排其路径和分流系数。

上述讨论从滤波器插入损耗，也即谐波衰减（或补偿）效果入手，提供了一个关于基本结构有源滤波器的功能和局限的统一描述，从而为以下进一步的讨论提供了基础，也为根据应用场合和补偿对象的要求选择适用的有源滤波器拓扑提供了一个参考。由于插入损耗的概念不是很直观，实际中可以采用谐波改善率来对有源滤波器的效果进行评估，定义谐波改善率为

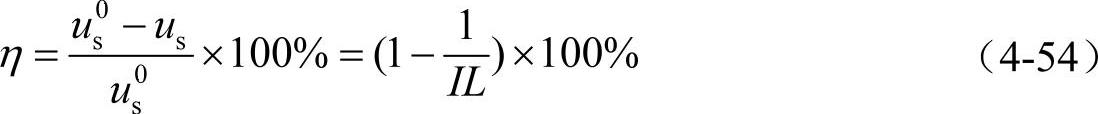
此时I型结构的谐波改善率就可以表示为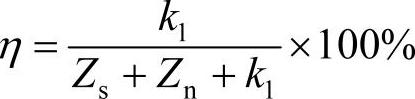，随着k₁→∞，谐波改善率趋近于100%，即实现完全补偿。较之插入损耗，谐波改善率可以更为直观地得到采用有源滤波器后抑制谐波电流的效果，以及如何选择适当的参数来提高补偿效果。其他类型的改善率可以参见表4-13。

2.并联有源滤波器

（1）原理与结构 图4-24给出了用于谐波电流滤波的并联有源滤波器结构图，是有源滤波系统的一种最基本的结构，包括构成有源滤波器核心的电压源（或电流源）逆变器、与系统耦合的变压器（或电抗器），以及相应的检测控制电路。图中串联电抗L_AC设置在非线性负荷的电源侧，以保证有源滤波器工作的稳定性和可靠性。

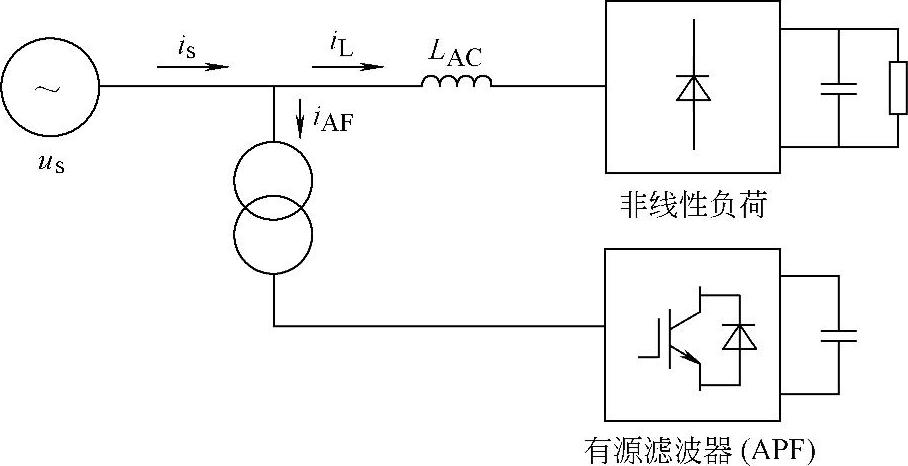
图4-24 并联有源滤波器原理图

有源滤波器通过向系统注入与欲补偿的谐波电流大小相等、方向相反的电流，与系统中的相应电流分量抵消，从而达到“滤波”的目的。并联型有源滤波器（APF）由于通过耦合变压器并入系统，不会对系统运行造成影响，具有投切方便、灵活以及各种保护简单的优点。其工作原理可以根据图4-25所示的等效电路图，以电压源逆变器为例分析如下。

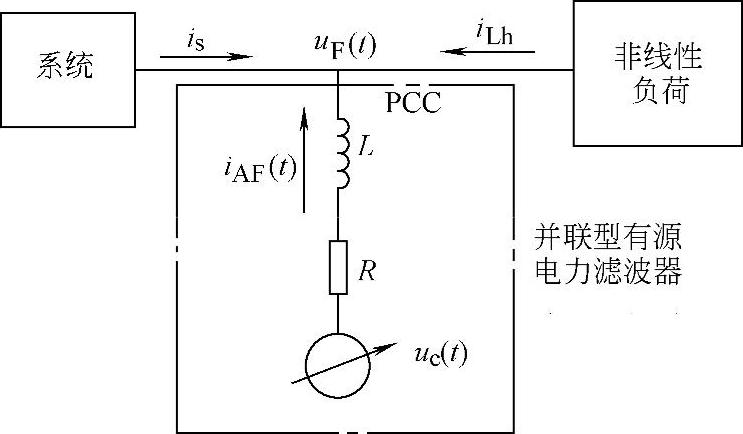
图4-25 并联有源电力滤波器等效电路

电压型逆变器产生的补偿电流i_c（t）满足下面的等式：

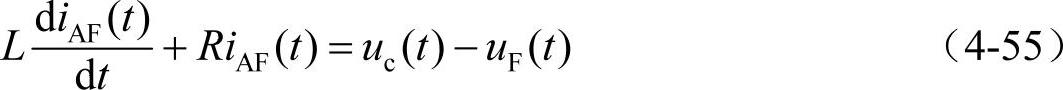
式中，u_c（t）、u_F（t）分别为逆变器和有源电力滤波器的输出电压；L、R分别为等效的电感与电阻。通常情况下，等效电阻R很小，因此可以忽略。所以近似有

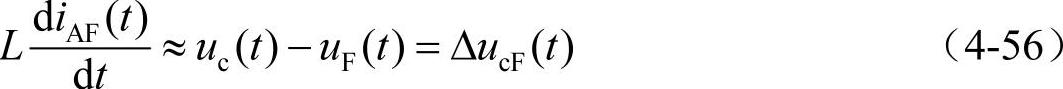
因此，有源电力滤波器产生的补偿电流大小主要取决于逆变器的输出电压u_c（t）的大小。根据电压源逆变器的调制控制理论，可以将电压源逆变器等效为一个比例放大器，即

u_c（t）=K_mu_dc（t） （4-57）

式中，u_dc（t）为电压源逆变器的直流侧电容电压；K_m为与调制控制方法有关的函数。

对于并联型有源电力滤波器，其主要的功能是补偿电流i_AF能快速跟踪负荷电流中的谐波分量，从而使流入电网的谐波电流尽可能小，以减少对系统的污染。而为了使i_AF能够快速跟踪要补偿的电流，需要满足两个条件：首先，i_AF的幅值要满足最大补偿电流的要求，即有源电力滤波器的补偿容量满足负荷补偿的要求；其次，有源滤波器输出电流的变化率di_AF（t）dt要大于谐波电流的最大变化率，以确保快速跟踪谐波电流的变化。这可以通过两个办法解决，即减小有源电力滤波器的等效电感L，或提高逆变器输出电压u_c（t）以加大电压差。耦合电感L越小，其电流跟踪能力越强，但是L过小，会导致输出信号中含有大量开关频率的特征谐波分量，并降低故障时的可靠性。因此，提高直流侧电容电压u_dc（t）成为提高有源电力滤波器电流跟踪能力的有效手段。

该滤波器通过变压器（或电抗器）与非线性负荷并联连接，对其特性的可以简述如下：

①逆变器应当包括一个辅助的、频带达1kHz的电流环，并且采用载波频率为25kHz的PWM方法，对补偿电流i_AF进行控制。上述条件使得滤波器可以对高达25次的谐波电流进行有效的补偿。对于整流器类的非线性负荷而言，由于主导谐波为5次，往往需对其加以特别关注，这一点在以下的讨论中将会专门加以说明。

②控制电路应当能从非线性负荷电流i_L中利用数字信号处理的方式，尽可能精确地瞬时提取欲补偿的谐波分量i_Lh的幅值和相位的信息。对于三相平衡负荷而言，这可以借助瞬时有功和无功理论实现。由于同步坐标变换可以将欲补偿的频率分量转换为直流，从而便于和其他分量区别，所以通常需要采用锁相环（PLL）来保证变换与电源的频率、相位的同步。

③为了从补偿电流i_AF中消除PWM逆变器开关频率的脉动，所以一般与逆变器并联一个小容量的无源滤波器。其安装位置应当尽可能靠近逆变器。

（2）控制系统有源电力滤波器控制系统由两大部分组成，即指令电流运算电路和补偿电流发生电路。其中，指令电流运算电路的主要功能是由补偿对象的电流中提取所需补偿的谐波和无功等电流分量，即所谓的谐波检测电路。补偿电流发生电路的作用则是根据指令电流运算电路得出的补偿电流的参考信号，构造实际的补偿电流。下面将分别加以说明。

1）补偿信号的检测方法：实际上，补偿器的补偿特性取决于由负荷电流中提取谐波的算法，即在很大程度上，APF的有效性依赖于是否能得到没有失真地表示欲补偿的谐波分量的参考信号。因此，APF控制关键问题之一就是找到一种算法，该算法可以由负荷电流中精确地提取欲补偿的谐波分量的幅度和相位，从而为控制提供参考。

并联有源滤波器通常包括三种类型的谐波检测方法，考虑到实际检测系统不可避免地存在的检测延时，实际中通常用一个一阶惯性环节来进行描述，这分别可以表示为

①负荷电流检测：该方法对位于有源滤波器接入点下游处的电流，即负荷电流i_L进行检测，然后从中提取谐波分量i_Lh。而实际补偿电流为

②电源电流检测：该方法对位于接入点上游的电源电流i_s进行检测，并从中提取谐波电流分量i_sh。而实际补偿电流为

③母线电压检测：该方法检测接入点处的母线电压u_pcc，然后从中提取谐波电压分量u_h。实际补偿电流仍为

通常，谐波提取技术可以分为两类，一种为直接法，即采用陷波滤波器将基频及不计划由APF补偿的低次谐波信号从所采集的信号中滤出，剩余的信号即可作为APF控制器的参考信号；另一种则为间接法，即将除干扰信号外的所有信号均由输入信号中取出，进行解耦，然后重新将所需的分量进行组合以作为参考信号。

a）陷波器（带阻滤波器）：基于陷波器原理的APF如图4-26所示，负荷电流i_L经采样后生成的采样信号i^s_L通过调谐于基频的陷波滤波器后，采样信号中的基频分量i^s₁被消除，而在参考信号中仅含计划补偿的谐波分量。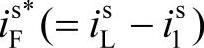

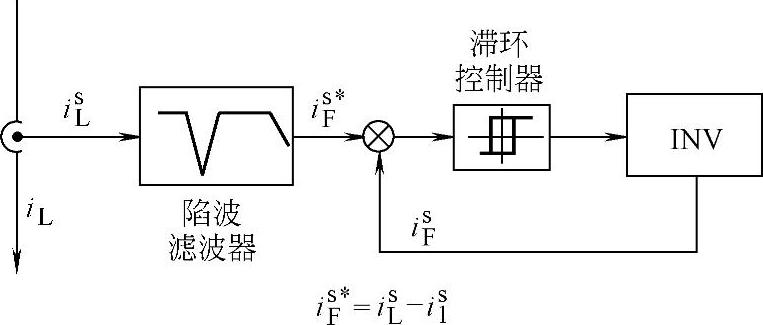
图4-26 基于陷波器的有源滤波器结构图

为了在没有失真的条件下滤出基频分量，需要采用窄带陷波器，但实际滤波器由于受到陷波器幅频和相频特性的影响，输出信号会发生失真，即上述简单的结构就不能实现理想的补偿。特别是窄带陷波器往往意味高阶滤波器，而这也表明对各次谐波分量造成更严重的互不相同的相移和幅度衰减，所以其无失真的提取需要大量的计算或昂贵的硬件结构。一个可行的方法是采用自适应滤波器。图4-27是一个采用IIR（无限脉冲响应）陷波滤波器的框图，为了克服上述问题，它采用了一个匹配滤波器，该滤波器可以完成上述陷波功能又不会引起附加失真，但由于牵涉大量计算从而限制了响应速度。

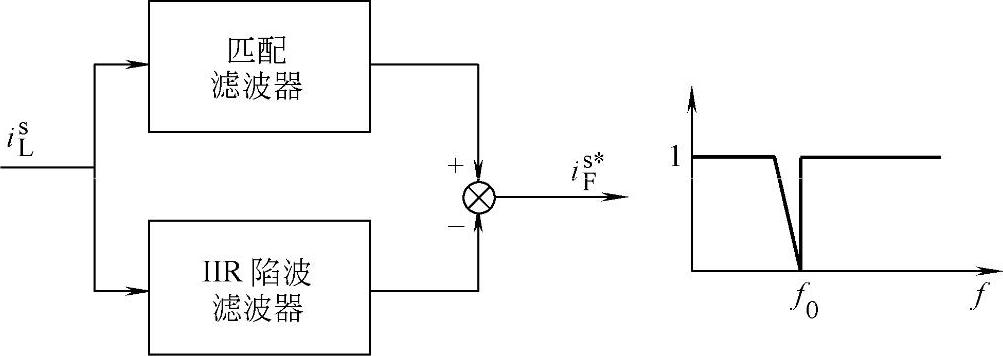
图4-27 自适应噪声滤波器

b）分解合成方法：图4-28给出了利用对采集信号的谐波分量解耦然后再组合构成的滤波器，它仅使所需补偿的分量通过，经组合后形成补偿器的参考信号。

图4-28a为采用多个调谐陷波器的方案，图4-28b是采用硬件FFT。但由于两者的硬件结构较为复杂，所以仅适用于计划消除某些特定谐波的项目。

c）自适应噪声对消：为了实现实时控制，三相有源滤波器的谐波检测目前普遍采用的是基于瞬时无功理论的谐波检测；但上述方法对于单相有源滤波器难于使用。一种可能的间接采样的例子就是所谓的自适应噪声消除方法（ANC）。这种方法的结构和幅频特性如图4-29所示，其特点是利用电网基频信号作为参考信号，对负荷电流中与参考信号同频率同相位的信号产生陷波作用，使输出信号仅含除参考信号外的谐波与无功功率分量，并以此作为有源滤波器的控制信号。

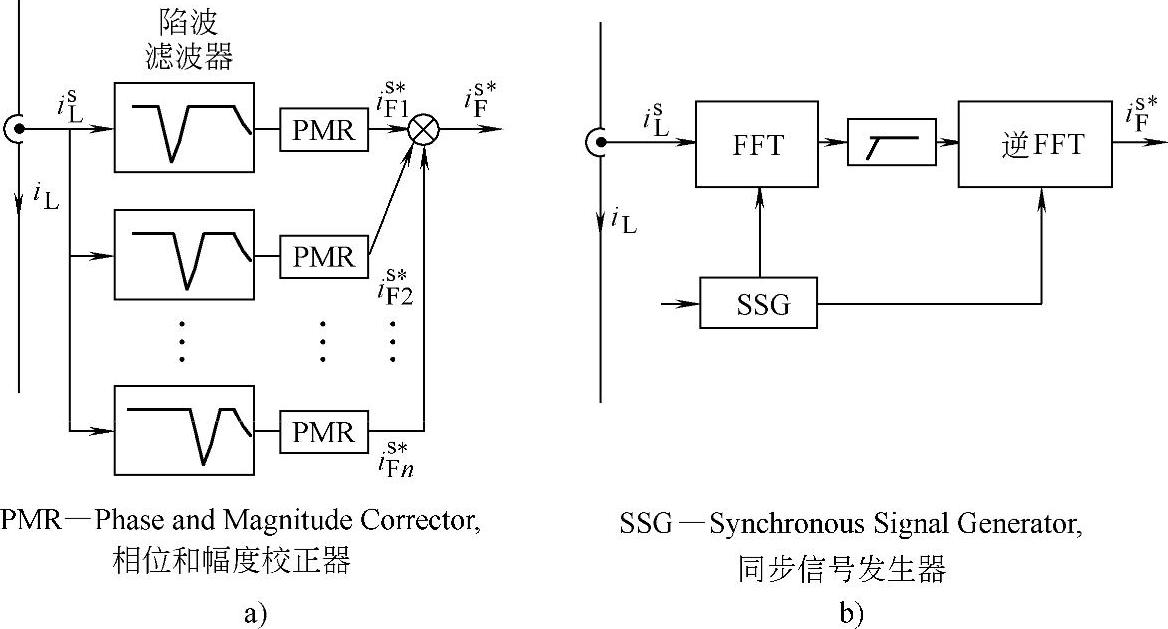
图4-28 谐波解耦组合滤波器

a）带通滤波器 b）FFT解耦方法

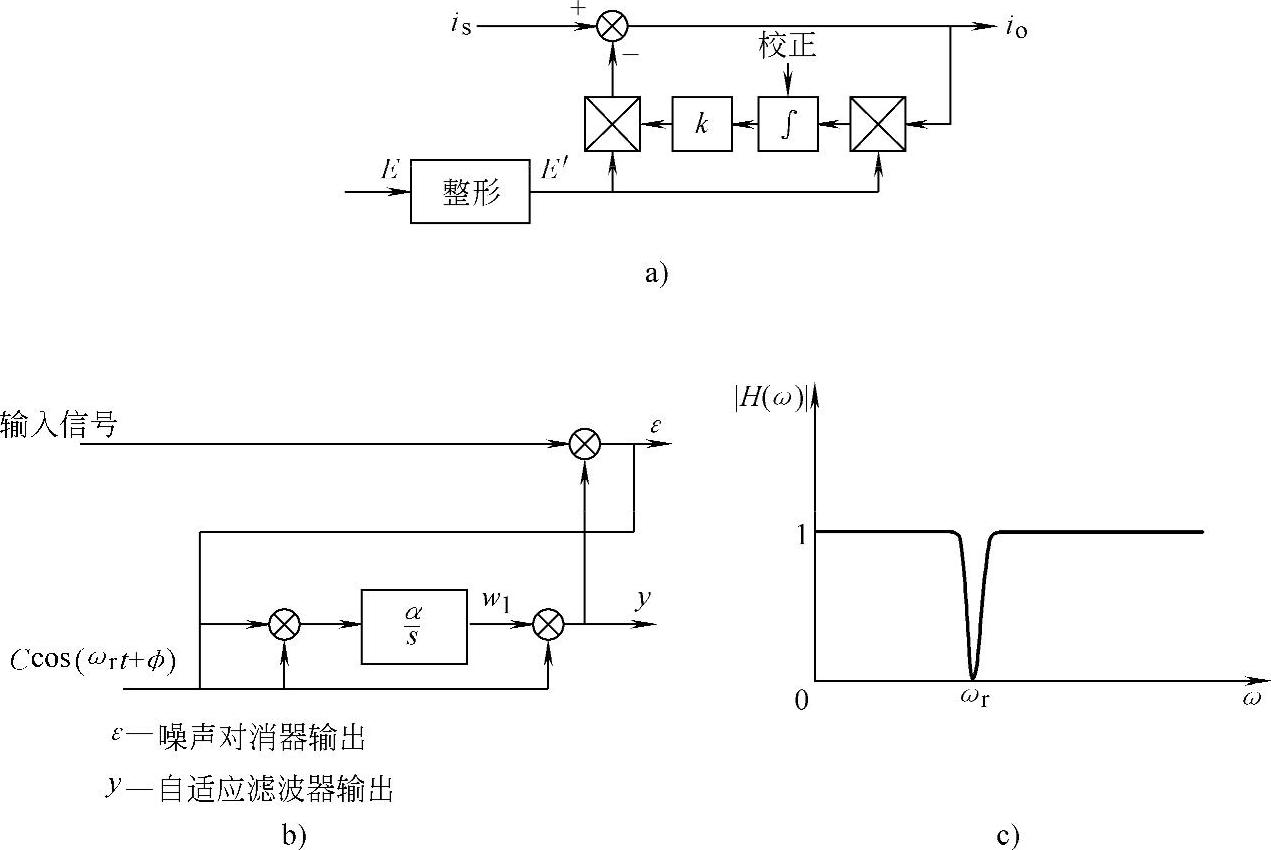
图4-29 自适应噪声滤波器原理图与传递函数

a）自适应检测电路原理图 b）数字实现原理图 c）频率特性

i_o为谐波检测电路的输出；E为电网电压，通常为标准正弦基波电压E=E_msinωt，从图4-28可得：

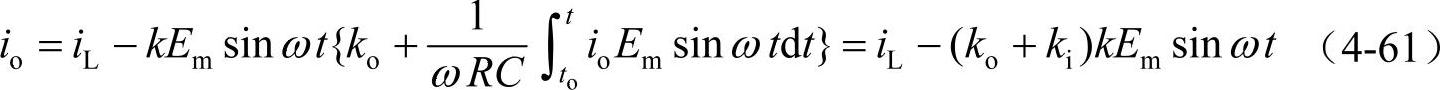
式中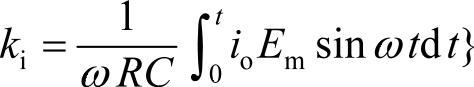，；k为比例系数，k_o为积分器输出的直流分量，当稳态时，k_o保持恒定值不变；k_i为积分器输出的交流分量，由于正交原理及积分器的时间常数很大，积分后除基频正序分量，该分量为与E′同频率且同相位的正弦分量，此外所有其他分量均趋于零。而由于积分器输出中的直流分量经比例放大器和乘法器后产生与i_o中正弦基波分量相对应的正弦基波分量，再经反相求和运算，抵消i_o中的正弦基波分量，直至i_o中不再含有与E′同频率的正弦分量时，积分器输出的直流分量将保持在某个值不变，此时检测电路进入稳定状态。故稳态时输出信号中基频分量为零，所以最终作为积分器稳态交流输出的k_i也将近似为零。

假设负荷电流 i_L=i_p+i_q+i_h （4-62）

式中，i_p为基频有功分量；i_q为基频无功分量；i_h为谐波分量。如前所述，稳态时i_o不含有与电网同频率的基频分量，故

i_o=i_L-kk_oE_msinωt=i_L-i_p=i_q+i_h （4-63）

可见，检测电路的输出i_o即为负荷电流中的无功分量及谐波分量。该电路的优点是适应范围广，稳态检测精度高，检测精度不受电网基波频率变化影响，且硬件实现简单，易于调整。同时，可以根据需要，分别检测负荷中的谐波和无功功率。其缺点是动态响应较慢，同时因硬件电路中运放等器件的零漂影响，实际电路中需加校正装置。

对于非线性负荷所产生的噪声，上述方法均可望取得良好的效果，但应当注意的是，由于往往APF与输电线的耦合需经变压器实现，而常规的铁心变压器及其漏抗的非线性对谐波的衰减作用将严重影响到补偿效果。一般而言，13次及以下谐波受铁心变压器影响不大，对于更高次谐波的补偿则需注意铁心材料的选择和变压器的设计。

d）瞬时无功功率：基于瞬时无功功率算法对电源电流或负荷电流的基频分量或特定频率分量进行检测的方法将在第5章进行详细的讨论，这里就不再重复；采用该方法可以在同步坐标系上将特定频率的分量变换为直流分量，然后通过低通滤波器将相应分量检出，就可以得到所需补偿的电流指令，如图4-30所示。

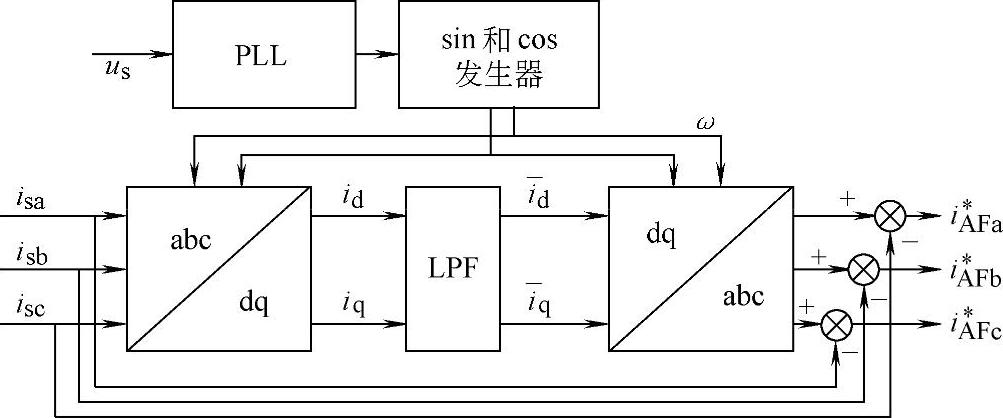
图4-30 基于同步坐标系的瞬时电流计算方法

图4-31为一个典型的采用空间电压矢量PWM调制方法的控制系统框图。图中，LPF表示低通滤波器，PLL为锁相环，abc/αβ表示补偿器的三相/两相变换，SV PWM表示空间电压矢量PWM调制。据统计，日本在实用的有源滤波器的控制中采用瞬时空间矢量法的系统占总数的84%^[7]。可见对上述方法的充分研究是十分重要的。

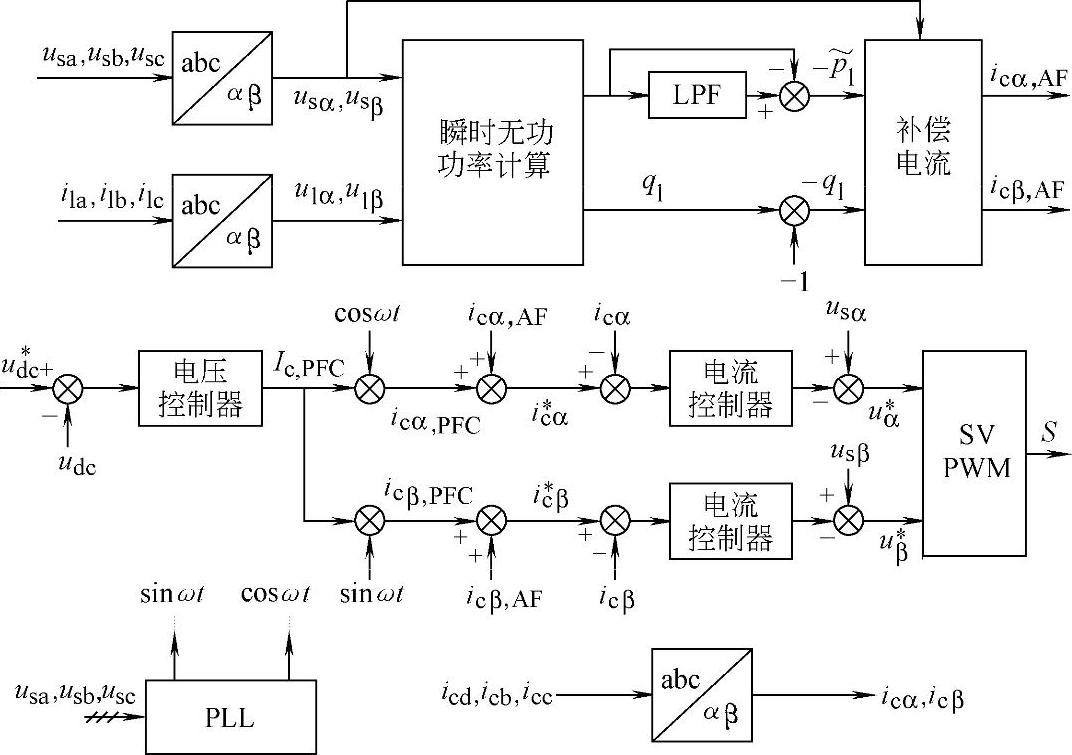
图4-31 并联有源滤波器控制系统框图^[7]

2）控制系统结构：下面分别对采用三种不同谐波信号检测方法的闭环控制系统分别加以讨论^[9]，其中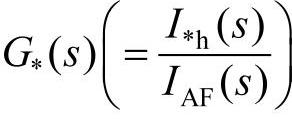表示不同的控制系统的开环传函。为了便于比较，额定输出功率均选为2.99MW。(www.xing528.com)

①基于负荷电流检测的控制系统：采用负荷电流检测的闭环控制系统如图4-32a所示，其对应的波特图见图4-32b所示。波特图显示，该方法的相位裕量仅为6°～7°，在实际系统应用中考虑到控制延时，这可能导致系统的不稳定。

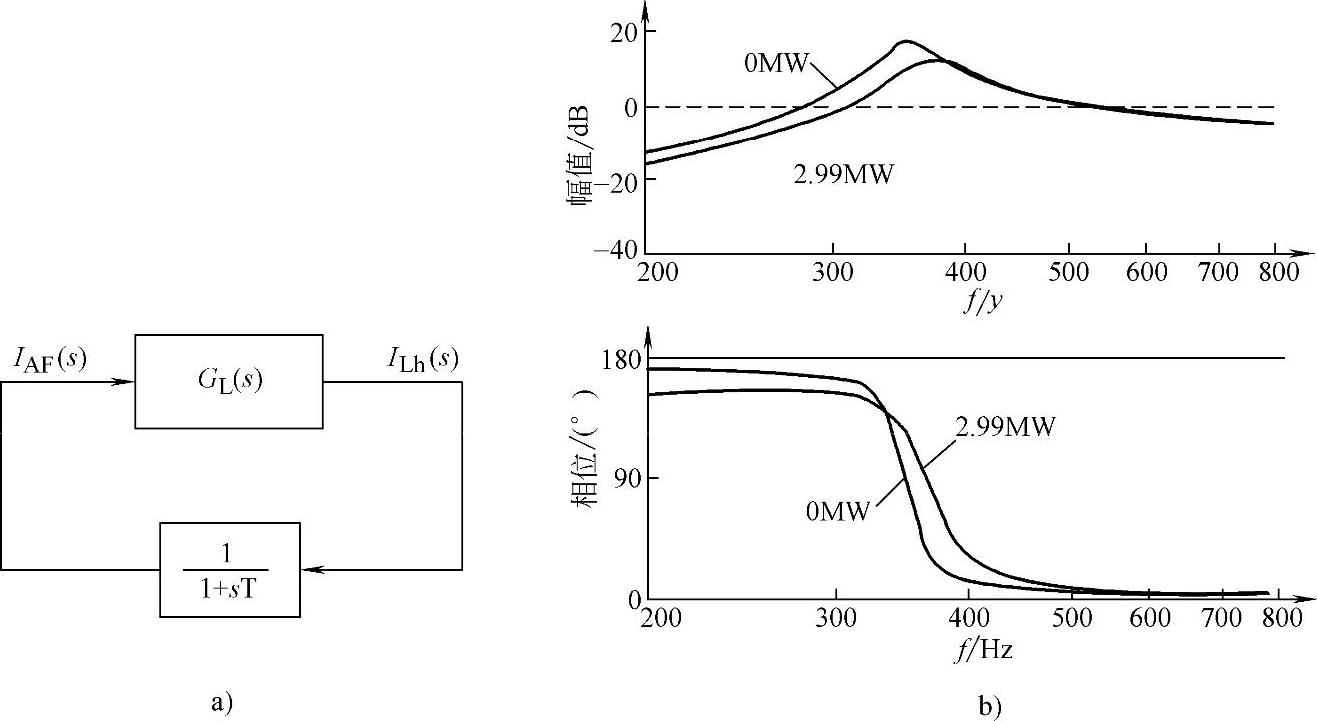
图4-32 基于负荷电流检测的控制系统

a）系统框图 b）G_L（s）波特图

②基于电源电流检测的控制系统：相应的框图和波特图见图4-33。其中，k_s=20。

根据波特图，在额定负荷时相位裕量为37°，但是在空载时上述裕量下降到22°，同样可能引起系统的不稳定。

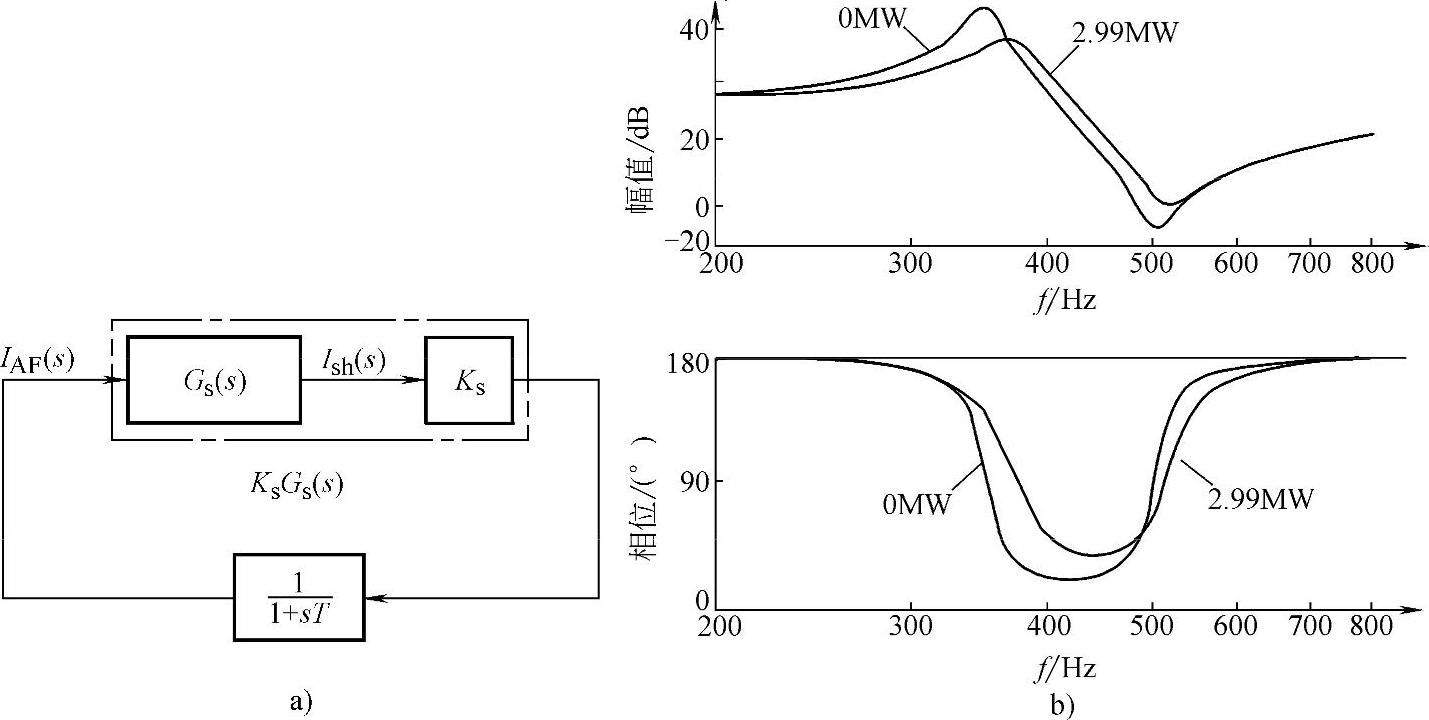
图4-33 基于电源电流检测的控制系统

a）系统框图 b）K_SG_S（s）波特图

③基于母线电压检测的控制系统：母线电压检测的闭环控制系统框图和波特图如图4-34所示，其中K_u=2。由于相位裕量始终在90°以上，所以检测母线电压的有源滤波器控制方法是稳定的，仿真研究表明，即便控制延时达到0.16ms，即接近一个周期，系统仍然相当稳定。由此，从稳定性角度出发，母线电压检测方法是最适于配电系统并联有源滤波器的控制方法。当将其安置在非线性负荷附近时，可以有效地消除接入点的谐波电压。而如果希望利用并联有源滤波器来阻尼沿馈线传播的谐波的话，其最佳安装位置为一次线的终端。

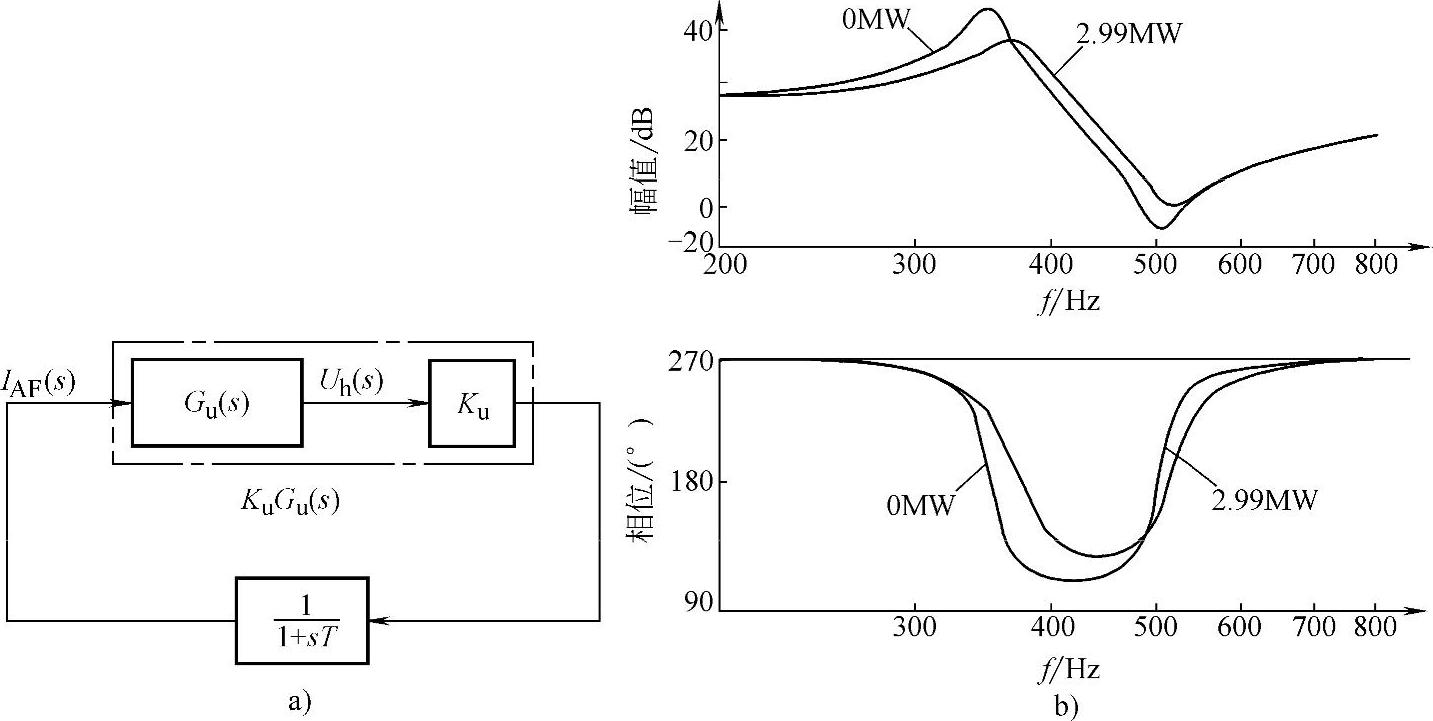
图4-34 基于母线电压检测的控制系统

a）系统框图 b）K_uG_u（s）波特图

参考文献[7]中Akagi给出的一个“纯”有源滤波器的实施例可以对上述讨论作一个总结。该滤波器的目的是，将电源电流i_s的谐波含量降低到5%以下。由于滤波器本身与电网直接连接，所以逆变器的输出电压u_AF中将包含接入点电压u_pcc。

图4-35给出了纯并联有源滤波器的电路图。非线性负荷也采用一个整流器负荷表示。补偿装置为一个三相并联纯有源滤波器。电路中，有源滤波器不是通过变压器而是串联耦合电抗器L_F接入系统的。由于需要直接接入480V交流系统，直流侧电压采用750V。为了达到良好的补偿效果，采用了频率为10kHz的载波信号。

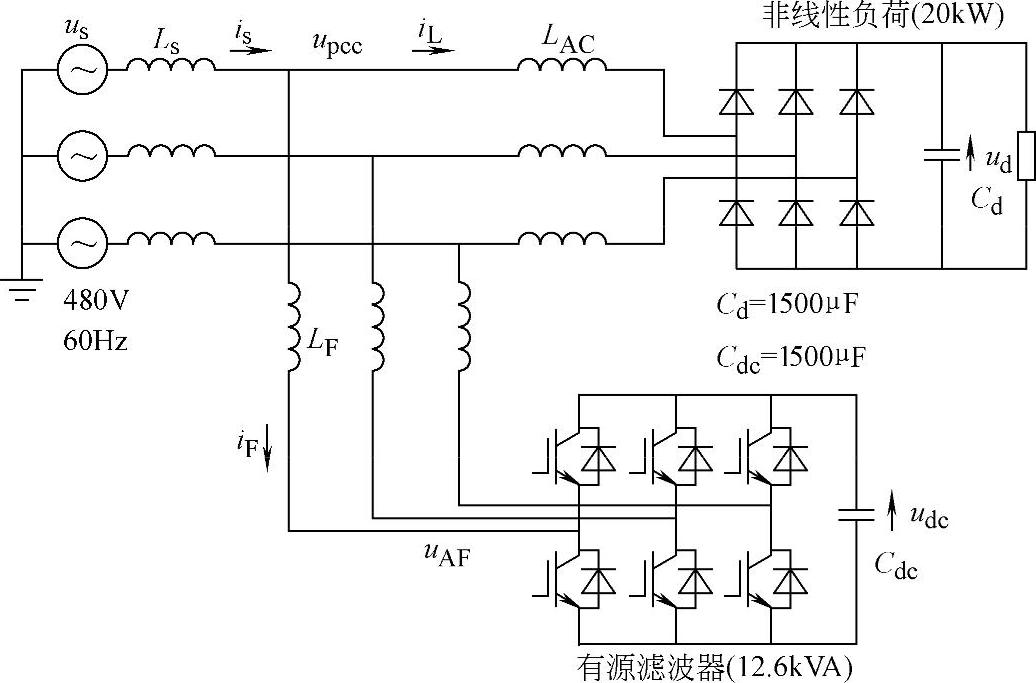
图4-35 纯并联有源滤波器电路图

纯有源滤波器的额定功率可以计算如下：

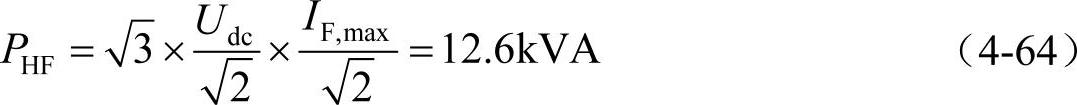
式中，I_F，max是滤波器电流的最大值。

上述纯有源滤波器的控制器包括三个部分，即反馈控制、前馈控制和直流电压控制。其系统框图如图4-36所示。

反馈控制的目的是通过检出需要补偿的谐波电流，其中d₁-q₁变换模块通过同步坐标变换将流入电网的三相电流i_s，abc转换为瞬时有功电流i_d1和瞬时无功电流i_q1。此时电网电流中的基频分量呈现为直流分量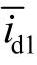、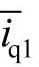，而其中的谐波分量则呈现为交流分量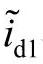、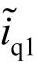。通过两个截止频率为16Hz的一阶高通滤波器（HPF）提取出对应于谐波分量的交流分量，然后经过d₁-q₁逆变换提取出电源侧三相谐波电流分量，对常规并联型有源滤波器而言，如图4-36所示，由于以注入系统的电流作为补偿信号，所以实际上就已经完成了滤波器补偿电流参考值的计算。

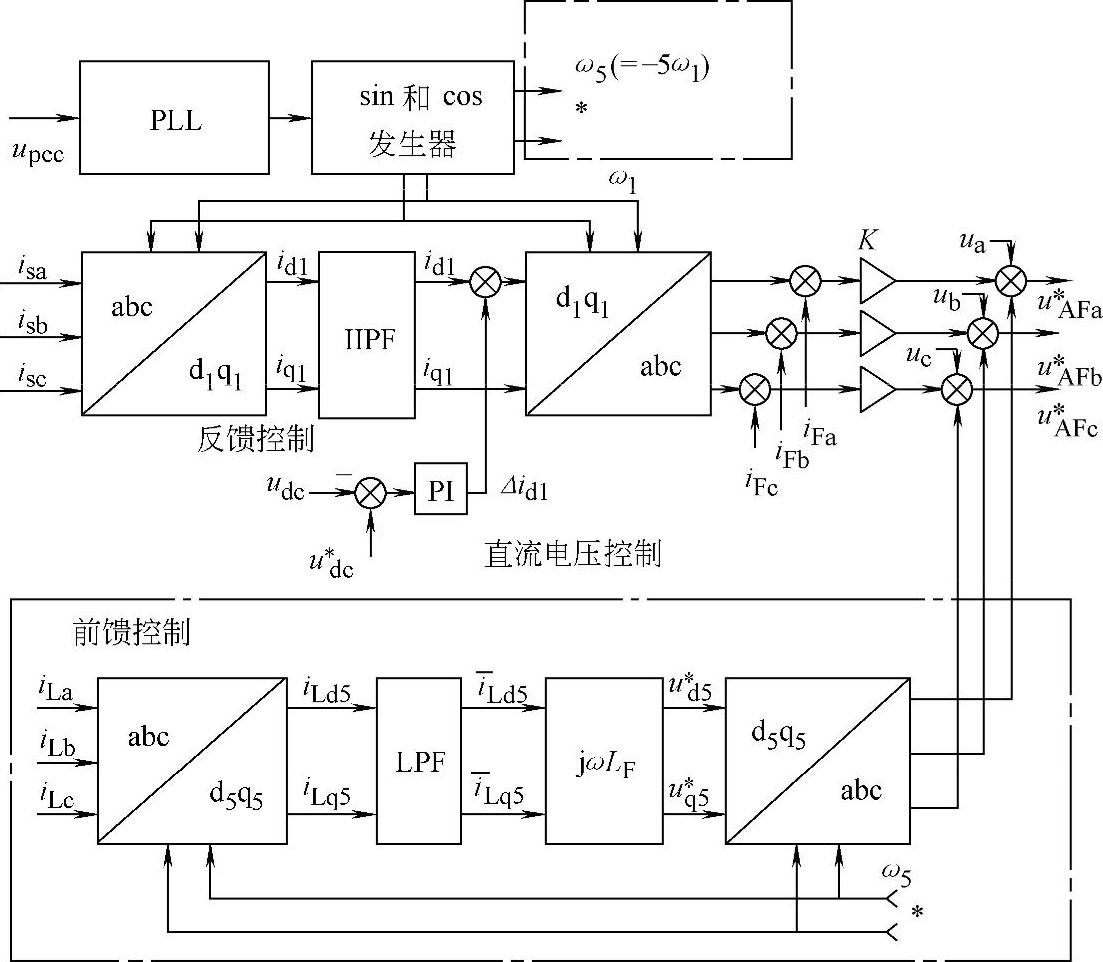
图4-36 纯并联有源滤波器控制系统框图

文献[9]则采用了另外两个与常规作法不同的、十分新颖的措施，一是以补偿器输出电压作为控制目标，所以接入点电压成为逆变器输出电压的一部分。为了实现上述控制，将谐波电流分量与流经耦合电抗（即有源滤波器）的电流i_F，abc相加，得到补偿器输出电流。该输出电流乘以放大系数K，得到有源滤波器在耦合电抗器L_F两端生成的电压的参考值：

该电压值和检出的公共连接点PCC处的电压u_a、u_b、u_c相加，得到有源滤波器输出电压的参考信号u^*_AF,abe。由于该算法将公共连接点的电压u_pcc作为控制信号的一部分，所以可以用来补偿该电压对谐波电流可控性的影响。

二是由于作为非线性负荷的整流器，其主导谐波为5次；为了更好地实现对其补偿，控制系统中专门设计了一个5次谐波的前馈控制环节（见图4-36中点画线框）。其功能是计算流经耦合电抗器L_F上的负荷的5次谐波电流引起的附加电压降。做法是，首先提取非线性负荷的电流i_L，abc，然后通过d₅-q₅变换得到以5次谐波频率同步旋转的同步坐标系上的负荷电流分量i_L，dq；此时5次谐波分量转换成直流分量，而其他分量仍为交流。然后通过两个截止频率为16Hz的一阶低通滤波器（LPF）得到作为直流分量的5次谐波的dq分量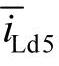、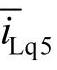，乘以耦合电抗ωL_F得到负荷电流在耦合电抗上引起的5次谐波电压分量的参考值u^*_d5、u^*_q5再经过逆变换得到耦合电抗器两端由于非线性负荷5次谐波电流所引起的三相谐波电压分量。该值进一步和前述反馈环节得到的电压信号u^*_AF,abe相加，得到新的、考虑到5次谐波在L_F上所引起的附加压降的有源滤波器输出电压的参考信号。更详细的讨论请参考文献[7，11]。纯并联滤波器的仿真波形如图4-37所示。

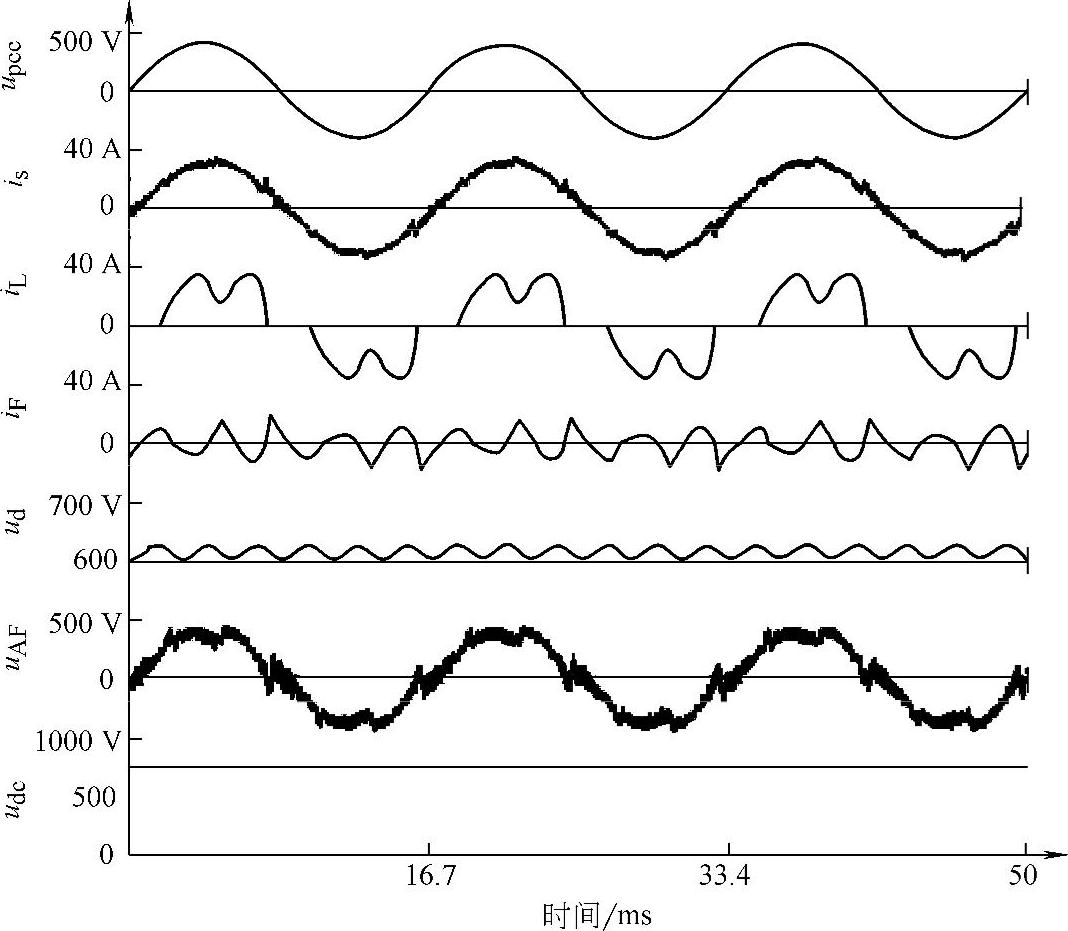
图4-37 纯并联滤波器仿真波形

需要指出的是，单纯从控制的角度而言，该前馈环节并不是必须的，略去图4-36中点画线包围的部分同样，可以达到类似的补偿效果。只是由于其他谐波的幅值与主导谐波相比可能相差太远，利用附加的前馈控制环节对主导谐波单独进行控制，可以降低反馈环节所需的放大系数，从而改善系统的稳定性。对于常规的有源滤波器而言，该部分很少采用。

直流电压控制用来维持直流电容上的电压，以为补偿器提供电压支持。因此，有源滤波器是通过控制电量Δd₁向直流电容提供基频有功功率，来控制直流侧电容电压。

参考文献[10]中提出了一个采用多重化技术和基于瞬时无功功率理论的反馈控制系统的并联有源滤波器，其结构如图4-38所示。该装置兼顾了补偿特性和器件开关频率的要求，对于中大容量的实际应用具有很好的前景。

随着功率器件和数字控制电路价格的不断下降，目前并联纯有源滤波器在电能质量控制领域已经具有良好的市场前景，但价格因素仍是制约其广泛应用的一个重要条件。目前10～400kVA容量的纯有源滤波器已经被应用在电力系统、工商企业和医院等领域。

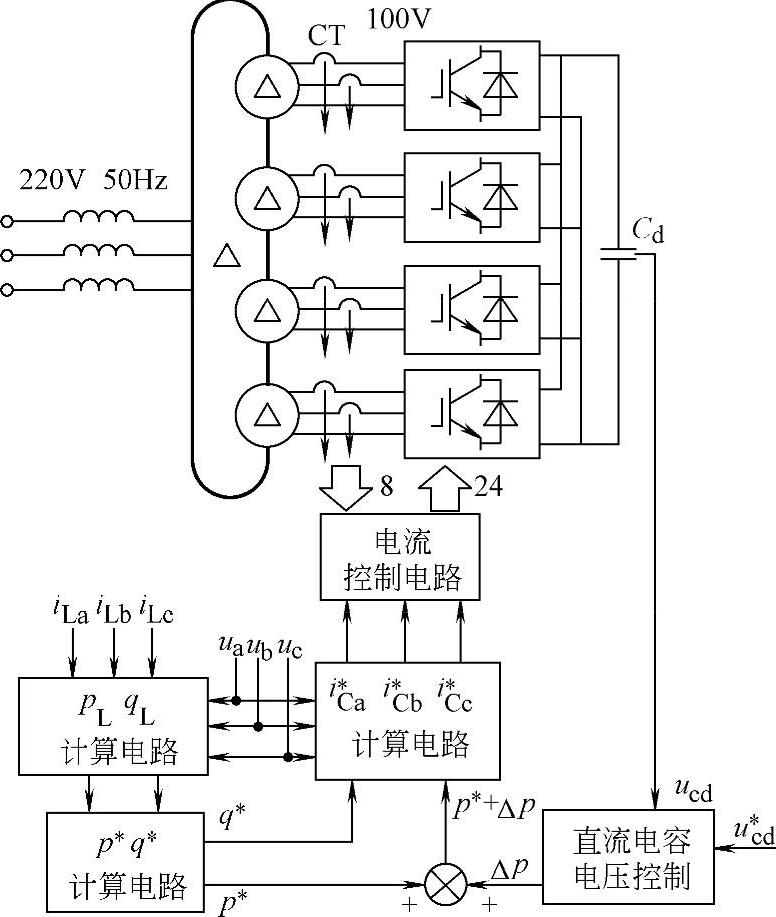
图4-38 四重化串联有源滤波器的结构和控制框图^[10]

3.串联有源滤波器

串联有源电力滤波器是串联在供电电源与非线性负荷之间的电能质量治理设备，其主要功能是电压调节，即当系统电压受到干扰时，串联有源滤波器将产生适当的补偿电压，使负荷侧电压不受系统电压变化的影响，如图4-39所示。这时，通常称为串联型电能质量控制器（Series Power Quality Controller，SPQC），也称为动态电压调节器。串联有源电力滤波器的另一功能是接在供电系统与非线性负荷之间，将系统与非线性负荷隔离开，同时在负荷侧并联无源滤波器，防止非线性负荷的谐波电流流入系统。此时串联有源滤波器的谐波阻抗大，非线性负荷的谐波电流都通过阻抗小的无源滤波支路分流了。

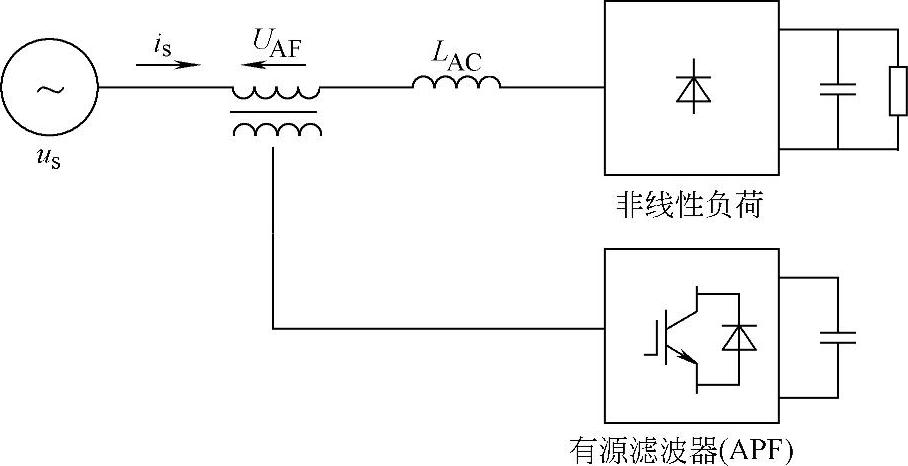
图4-39 串联有源滤波器原理图

图4-39所示的串联有源滤波器通过三相变压器或三个单相变压器串联到线路之中，是按以下反馈的原则进行控制：

1）控制器检测瞬时线路电流i_s。

2）利用数字信号处理的方式，从线路电流中提取需要补偿的谐波电流i_sh；所谓第一代的检测方法是利用基于同步坐标系的高通滤波器来提取谐波分量，但面临系统参数和控制时延带来的稳定性问题。第二代检测方法则是利用基于同步坐标系的低通滤波器，从信号中提取基频分量i_s1，然后利用i_sh=i_s-i_s1取得谐波分量。相对于第一代检测而言，可以有效地减小控制时延，进而提供稳定性。

3）有源滤波器的功能是在串联变压器两端施加一个补偿电压U_AF=-Ki_sh。当反馈增益K足够大时，相当于在线路中接入一个对于谐波分量而言呈高阻抗的元件，从而可以显著地减小线路的谐波电流i_sh。

串联有源滤波器采用的控制方式与并联有源滤波器相似，主要包括前馈和反馈两种，在此不再赘述。

4.统一电能质量控制器

如上所述，并联有源电力滤波器通常主要用来解决和电流相关的电能质量问题，如电流的谐波分量、无功分量和不平衡问题。而串联有源电力滤波器则用来解决与电压有关的电能质量问题，如谐波电压、电压暂升和暂降，以及电压不平衡问题。而目前电力系统中，往往是两者并存，因此通过共用中间直流环节将两者背靠背结合起来的串并联综合控制器，即所谓统一电能质量控制器（Unified Power Quality Controller，UPQC）得到了越来越广泛的认同^[12，13]。

UPQC的主电路结构如图4-40所示，包括串联有源滤波器、并联有源滤波器、直流储能单元三个部分。两个脉宽调制（PWM）逆变单元分别构成串联单元和并联单元的主要部分，直流储能装置则是两个逆变单元共用的，这三个部分共同组成一个完整的用户电力装置。其中，串联部分用来在公共连接点向线路插入一个与线路电流成正比的串联电压，从而一方面可以抑制线路电流中的谐波分量，另一方面又可起到缓冲器的作用，以消除线路电压跌落或闪变对负荷的影响。而并联部分则一方面用来通过直流中间环节向串联补偿器提供潮流控制所需的有功功率，另一方面可以对较低频率的谐波进行补偿。这种统一电能质量控制器从应用角度区分，又可分为两类：一类是面向系统的，往往安装在变电所附近，其中安装在变压器侧的串联部分主要用来在配电线路和变压器之间起谐波隔离作用，并且对公共连接点处的用户提供电能质量控制，而装设于线路侧的并联有源滤波器则用来对负荷侧的谐波、无功功率和负序电流提供补偿；另一类是面向负荷的，通常安装在负荷附近，用来抑制闪变、电压跌落等现象对位于其下游的敏感负荷的影响。从结构上，UPQC与输电系统的统一潮流控制器（UPFC）相似，但是两者不论从应用场合、补偿对象，还是容量上均有相当大的不同。

由于串并联谐波综合控制器的串联和并联两部分共用直流侧，因此电网和装置之间必须进行隔离，否则会出现电容直通、相间短路等情况。现有串并联谐波综合控制器采用的隔离方法，基本上都是在并联或者是串联单元接入系统的地方增加隔离变压器。但隔离变压器的应用会带来一系列负面影响，并且增加了装置的成本，所以近年来又提出了一种新型的三相串并联谐波综合补偿器，称为直流隔离串并联谐波综合补偿器（DC Isolation UPQC，DCI-UPQC）。

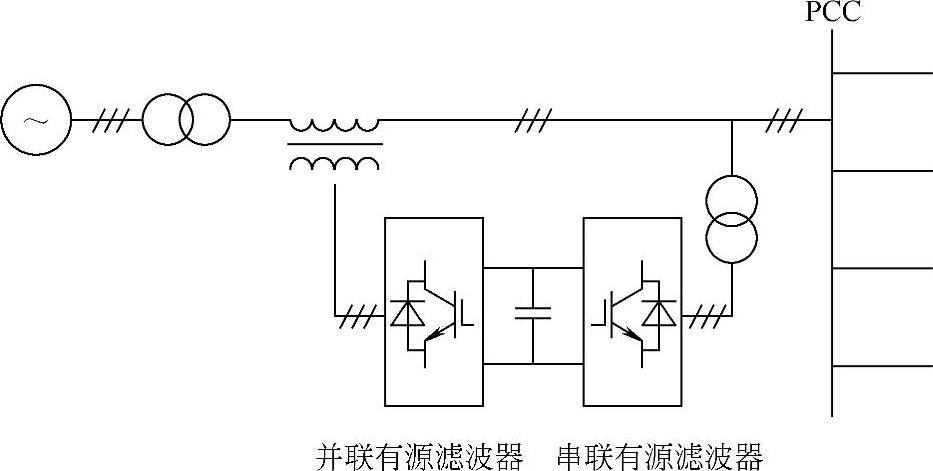
图4-40 统一电能质量控制器（UPQC）结构

DCI-UPQC的单相拓扑结构如图4-41所示。其结构的主要特点在于，它采用三组相同大小的电容互相并联（图中的C_s、C_com、C_p），电容之间采用电子开关进行连接（图中的S₁和S₂），开关S₁和S₂的开关状态互补。在S₁关断、S₂导通的时候，C_p和C_com进行均压；当S₁导通、S₂关断的时候，C_com和C_s进行均压，从而实现装置中串联单元和并联单元能量的交换。为避免在电容均压过程中充放电电流出现尖峰，在C_com支路上采用限流电阻或者是电感进行限流。

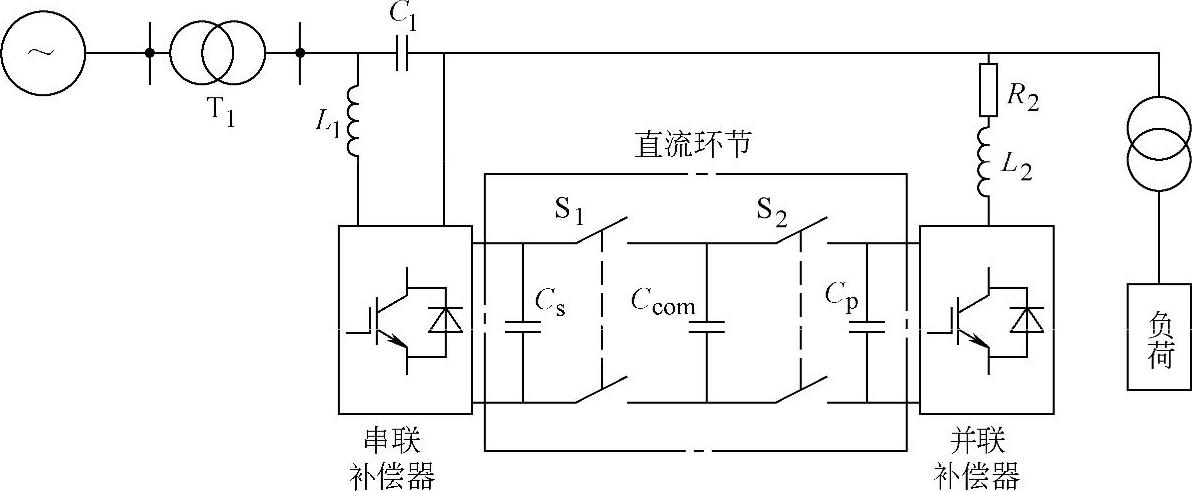
图4-41 DCI-UPQC单相拓扑结构

参考文献[14，15]提出的UPQC状态反馈方法是一个从理论和实际应用中均很有特色的方法，这里首先加以介绍。为了便于讨论，同样采用该参考文献中提出的原理框图，如图4-42所示。图中，6个逆变器利用状态反馈进行独立控制。

为了便于讨论，这里用串联理想电压源来表示串联有源滤波器，而以并联理想电流源来代表并联有源滤波器，来建立UPQC的等效电路^[14]。从结构上看，串联单元和并联单元的位置存在两种可能的选择，如图4-43所示。图中，PCC点的电压为u_t，负荷电压、负荷电流、电源电压和电源电流分别表示为u_L、i_L、u_s、i_s；而串联单元插入的电压为u_d，并联单元注入的电流为i_f。

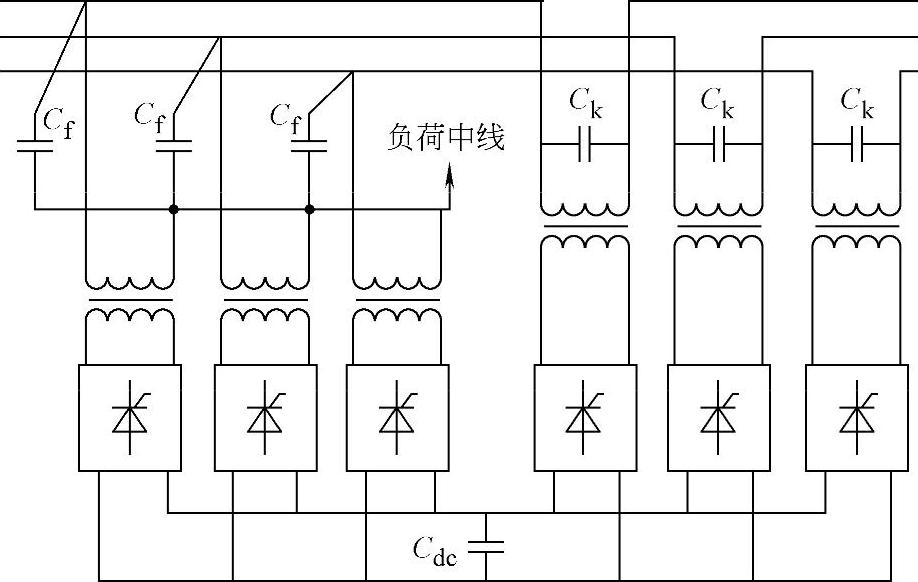
图4-42 UPQC原理框图

随着敏感负荷的应用日益广泛，电压不平衡和电压畸变引起的电能质量问题占了实际发生的电能质量问题的大多数，为了简化讨论，同时不失一般性，将讨论的重点放在电压畸变，而忽略谐波分量对负荷的影响，同时利用叠加原理对串联单元的电压补偿和并联单元的电流补偿分别讨论。讨论中，采用对称分量法，用下标0、1、2分别表示零序、正序和负序分量。

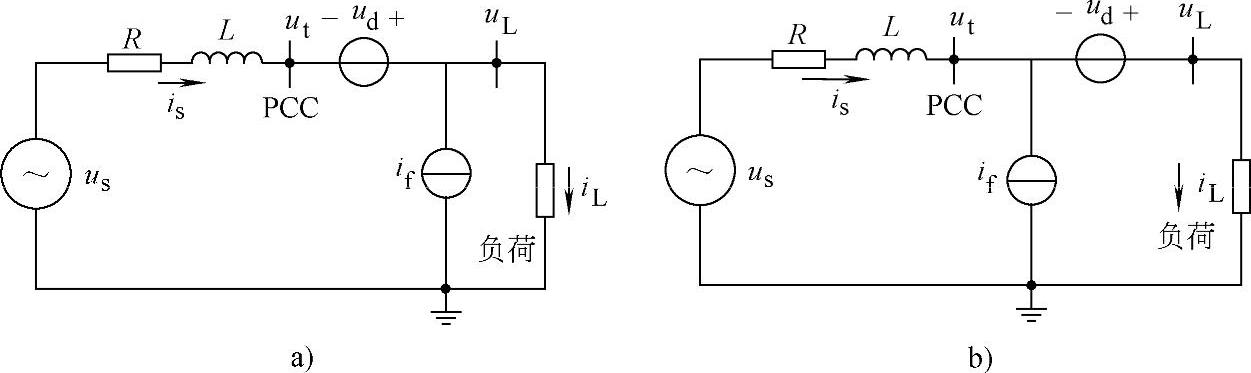
图4-43 串联单元和并联单元所处的位置

a）串联单元位于电源侧 b）并联单元位于负荷侧

首先假定电源电压不平衡，但不含谐波分量。此时由于

为了补偿由于电源电压的不平衡所造成的负荷端电压不平衡，对于三相四线制系统，串联补偿电源输出的电压需要能消除电源电压的零序和负序分量，即

为了使串联补偿器不需吸收额外的正序有功功率，故令其输出的正序电压与线路电流的正序分量I_s1正交，得

式中，α₁+jβ₁表示与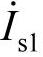正交的单位相量。进一步假设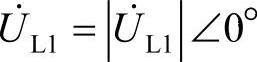，由此得到负荷端电压的二次方程为

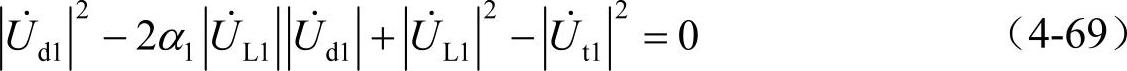
求解该方程得到的较小的解，即是为了补偿由于电源电压不平衡造成的负荷侧电压不平衡所需注入的电压。

而对于利用并联单元对不平衡电流的补偿，同样可以类似的方法得到

上述公式给出了UPQC对三相电流和电压不平衡补偿的计算公式。如果上述补偿是理想的，则流经串联补偿器的电流将完全是正序电流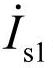，而由于串联补偿器插入的正序电压与流经该补偿器的正序电流相互正交，所以上述不平衡电压的补偿将不需要消耗任何正序功率。而由于上述补偿完全限制在正序范畴，所以也不产生任何负序和零序功率损耗。这说明上述正序电压补偿的平均功耗为零。而由于经过补偿后的负荷电压是严格正序的，而并联补偿中又不需注入正序电流，所以不平衡电流补偿所消耗的平均功率损耗同样是零。这说明串联单元位于负荷侧的UPQC在对不平衡进行补偿时，除了补偿装置本身的损耗所需的功率外，与系统之间没有任何有功功率的交换。对于串联单元位于负荷侧的UPQC可以用类似的方法进行讨论。

对上述串联单元位于电源侧和负荷侧两种UPQC结构的分析表明：

1）前者可以工作在零功率交换模式，后者不能。

2）前者可以通过调节并联补偿器输出的无功补偿电流使负荷端的功率因数为1，后者则取决于负荷本身。

3）前者的并联部分可以直接提供负荷所需的全部无功功率，而后者由于并联部分只能对接入点的无功功率进行直接补偿，所以只能提供负荷所需的平均无功功率。

图4-44为串联单元位于电源侧的UPQC等效电路。图中，负荷电阻与电感分别为R_L、L_L；为了改善控制的稳定性，在串联滤波器两端并联有L_d、C_d、R_d构成的滤波器，在并联滤波器两端引入电容C_f构成的滤波器；串联变压器的漏感为L_T，并联变压器的漏感和逆变器损耗L_f、R_f，电容C_d两端电压为u_sd，串联单元插入电压为u_d；直流环节电容电压为U_dc；串联和并联逆变器输出电压则分别表示为U_dcu_c1、U_dcu_c2。

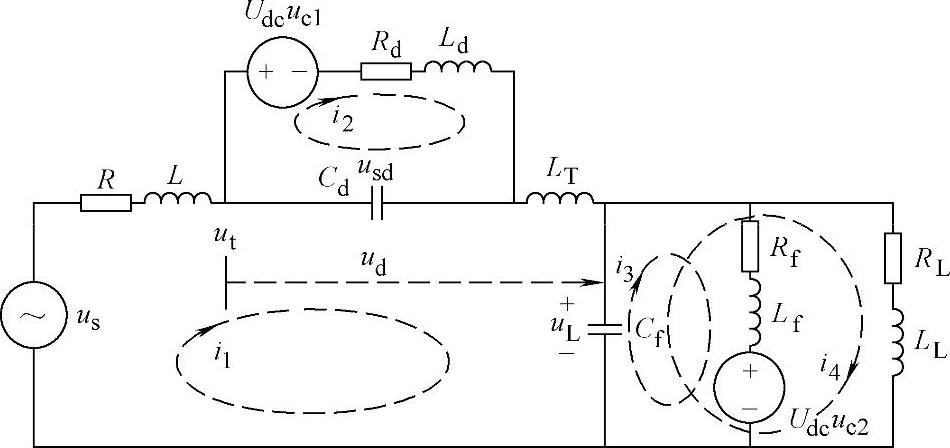
图4-44 串联单元位于电源侧的UPQC单相等效电路

图4-44所示系统的状态方程包括6个状态变量，即

式中

将状态方程式（4-71）改写为

式中，z=Px，而z^T=[i_fi_cfu_Li_Li_cdu_d]

而控制输入为u=-K（z-z_ref） （4-73）

式中，K是LQR增益矩阵，可以由矩阵PAP^-1和PB₁得到。上述系统可以利用滞环实现控制。而参考信号z_ref的选择需要根据网络理论谨慎地进行。其中，负荷电流i_L的参考值的选择最为困难，实践中往往采用降阶反馈控制的方法将其消去。详细的实现方法可以参见参考文献[14]，这里就不再详细讨论。

参考文献[15]给出了作者对串联补偿器位于负荷侧的系统进行的仿真研究。此时的等效电路如图4-45所示。采用如前所述的状态反馈得到的控制系统，仿真结果如图4-46所示。

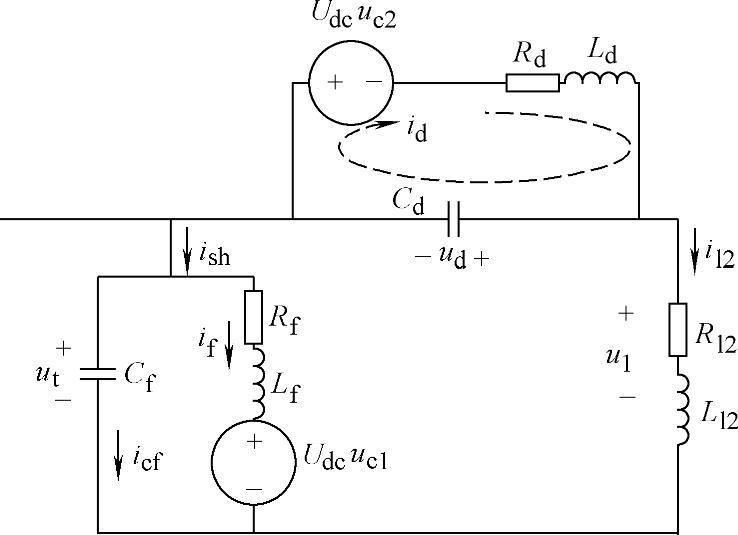
图4-45 串联单元位于负荷侧的UPQC单相等效电路

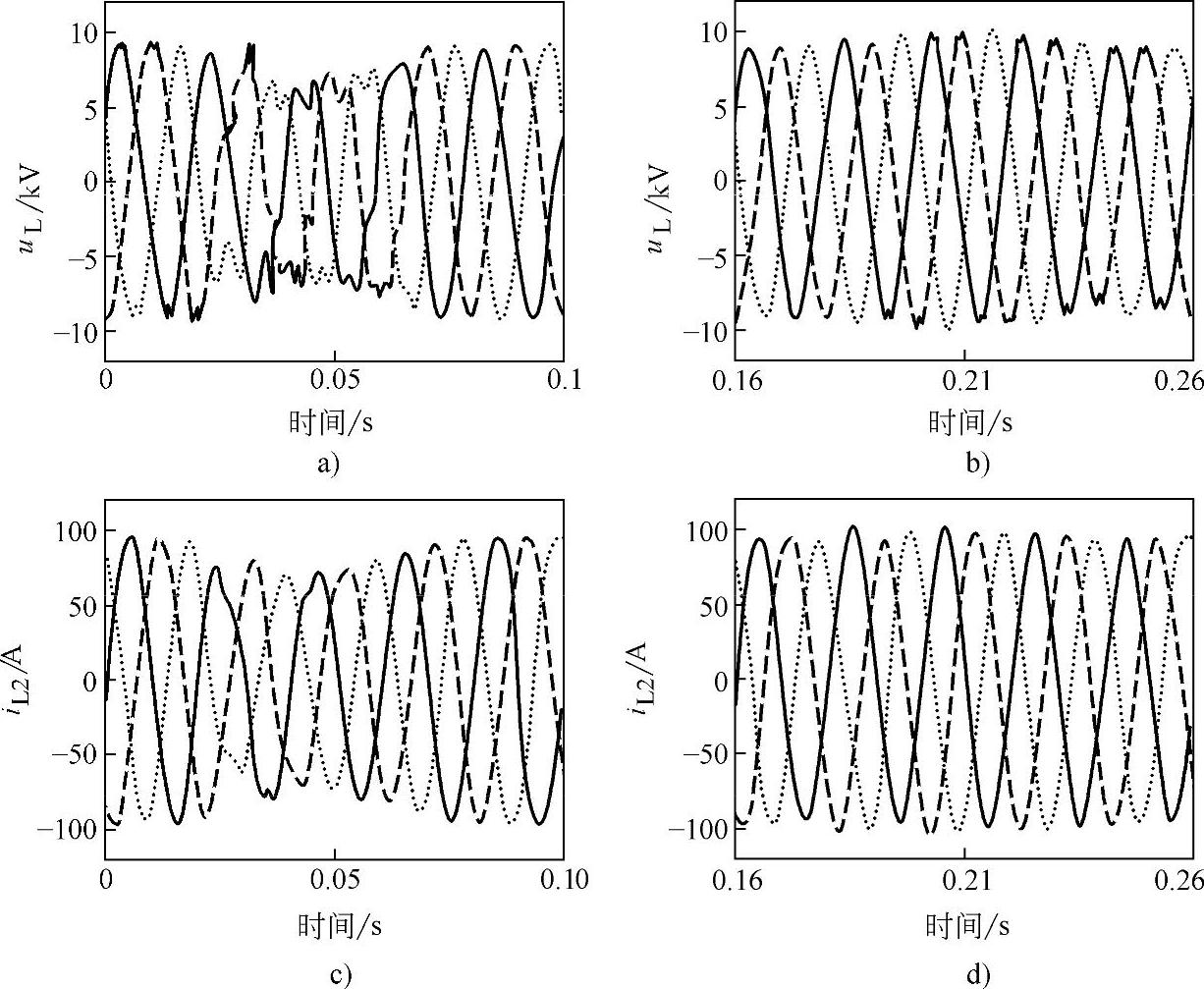
图4-46 电压暂降和恢复时负荷端电压、电流波形

a）、c）电压暂降时负荷端电压、电流波形 b）、d）电压恢复时负荷端电压、电流波形

设电源电压在稳态运行一个周波后突然跌落到标称值的一半，8个周波后电压又恢复到标称值。此时仿真结果如图4-46所示。可以看到，暂降发生后两个周波内，负荷电压和电感电流均发生下降，然后逐渐恢复到接近标称值。而在故障清除后，所需恢复的量已经很小。由此可以看到，UPQC在系统电压跌落时有极好的补偿作用，完全可以保护敏感设备不受电源电压扰动的影响。

同样在系统稳态运行条件下，系统电压在0.02s时发生突变，b相电压峰值维持在标称值9.0kV；a相电压的峰值跌落到7.0kV；c相则突升为11.2kV。4个周波后（0.1s），故障清除。仿真结果如图4-47所示。在该期间虽然接入点电压u_t呈现明显的三相不平衡，但是由于并联补偿器的作用，该点电压的不平衡度远小于电源电压的不平衡度。特别值得指出的是，负荷电压和电流基本维持平衡，显然补偿是成功的。而直流电容电压U_dc虽然呈现出一定的振荡，但其跌落的幅度不大。

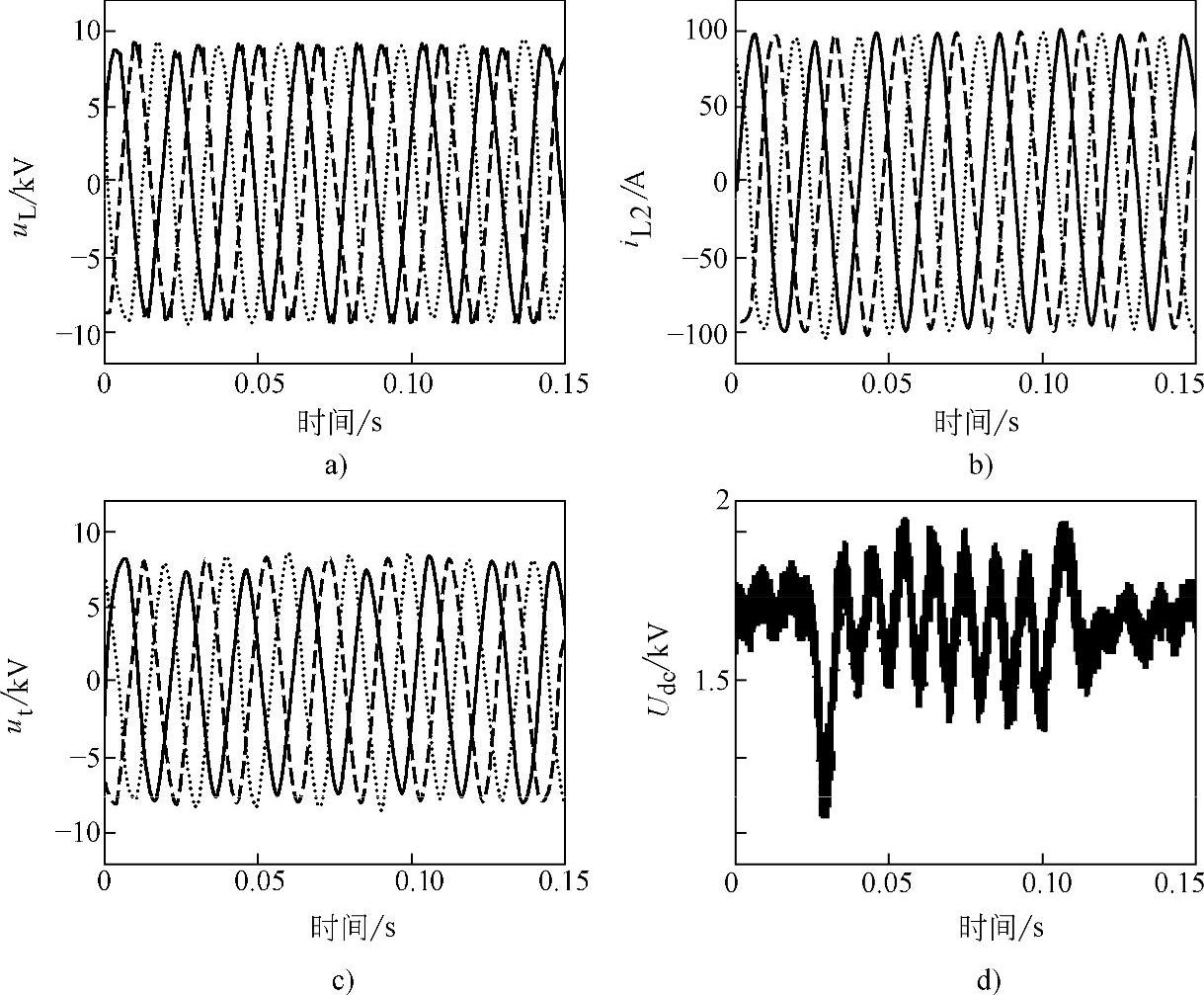
图4-47 三相不平衡暂降时系统响应

上述研究表明，采用上述式（4-73）给出的状态反馈方法，UPQC可以在有效地控制敏感负荷端电压的同时，还可以有效地校正母线电压，具有良好的补偿效果。上述研究还表明，由于当有源滤波器位于电源侧时，UPQC可以工作于零有功功率交换模式，所以直流电容电压的控制就得到了简化。但是对于任何结构的UPQC，电容容量的选择都是十分重要的，因为其存储的能量必须能在各种暂态过程中提供必要的电压支撑，而这就涉及容量的确定和控制策略的选择。