偏谐振式滤波器与滤波器组优化方案

1.单调谐带通滤波器设计

单调谐滤波器可以按照分流方式，即如前所述，将滤波器调谐频率选择某特征频率处进行设计。但实践中，为了防止滤波器与电力系统发生谐振，往往采取偏谐振式滤波器，并且其调谐频率低于计划抑制的特征谐波频率。其中，一种常用的方法是采用所谓的感性偏谐振滤波器^[12]，即将滤波器电感的值提高一个百分比ε（也称感性偏谐振率），此时滤波器电压谐振点为

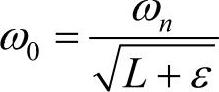
偏谐振时的阻抗公式为

简化设计时，可以取ε=δ_m，此时电压谐振点落在特征频率的（1-δ_m/2）标幺值处，从而避免了与电力系统发生谐振。取电容器为48μF，则调谐频率处电抗为

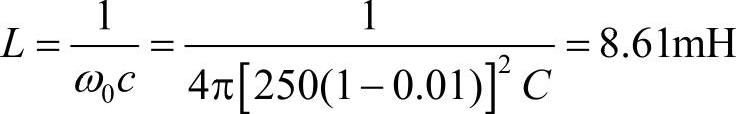
取电抗器的品质因数Q=60，电抗器的电阻为

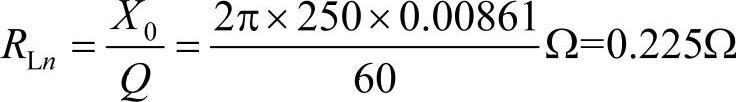
电容器的谐波电阻为

R_Cn=X₀tanθ=12.96×0.0008Ω=0.01Ω；R_fn=R_Ln+R_Cn=0.235Ω。实际的滤波器品质因数为

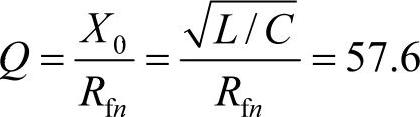
图4-17为上述方法得到的在不考虑接入点阻抗条件下滤波器的阻抗频率特性和考虑接入点阻抗条件下的系统综合阻抗频率特性。可以看到，由于系统阻抗与滤波器发生的并联谐振作用使得两者的特性有相当大的不同。

考虑到系统参数，一个对实际滤波器品质因数的估计方法如下^[12]：

式中，ϕ_s为电力系统谐波阻抗角，ϕ_s=arctan（X_sn/R_sn），该角随着负荷的增加而减小。比如当系统有中等负荷时，阻抗角ϕ_s为80°～82°；轻载时，ϕ_s取85°。

比如以偏谐振式简化方法设计一个中等负荷条件下的5次滤波器，此时取频率偏差δ_m=0.02，ϕ_s=80°，可以得到所谓最有利的品质因数^[18]为

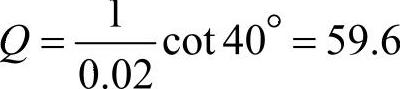
如前所述，由于系统电感L_s的存在，该电感和串联单调谐滤波器中电感和电容一起会产生频率低于滤波器调谐频率的并联谐振，其频率为

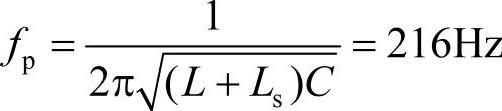
由图4-17可以看到滤波器自身的频率特性为在调谐频率f₀以下的低频区域，滤波器呈现容性，相位超前；而在调谐频率f₀以上的区域，滤波器呈现感性，阻抗在调谐频率f₀处呈现最小值。而考虑接入点短路容量时，上述并联谐振点处f_p阻抗急剧增大，而偏离该谐振频率f_p时，在高频和低频段阻抗均受到接入点短路阻抗的限制，所以呈现感性。滤波器接入点的短路容量对滤波器接入后系统的频率特性具有相当大的影响，所以在按参考文献[18]推荐的滤波器计算公式（此类公式通常不考虑接入点参数对滤波性能的影响）完成设计后，利用计算机仿真进行核算是必不可少的步骤。

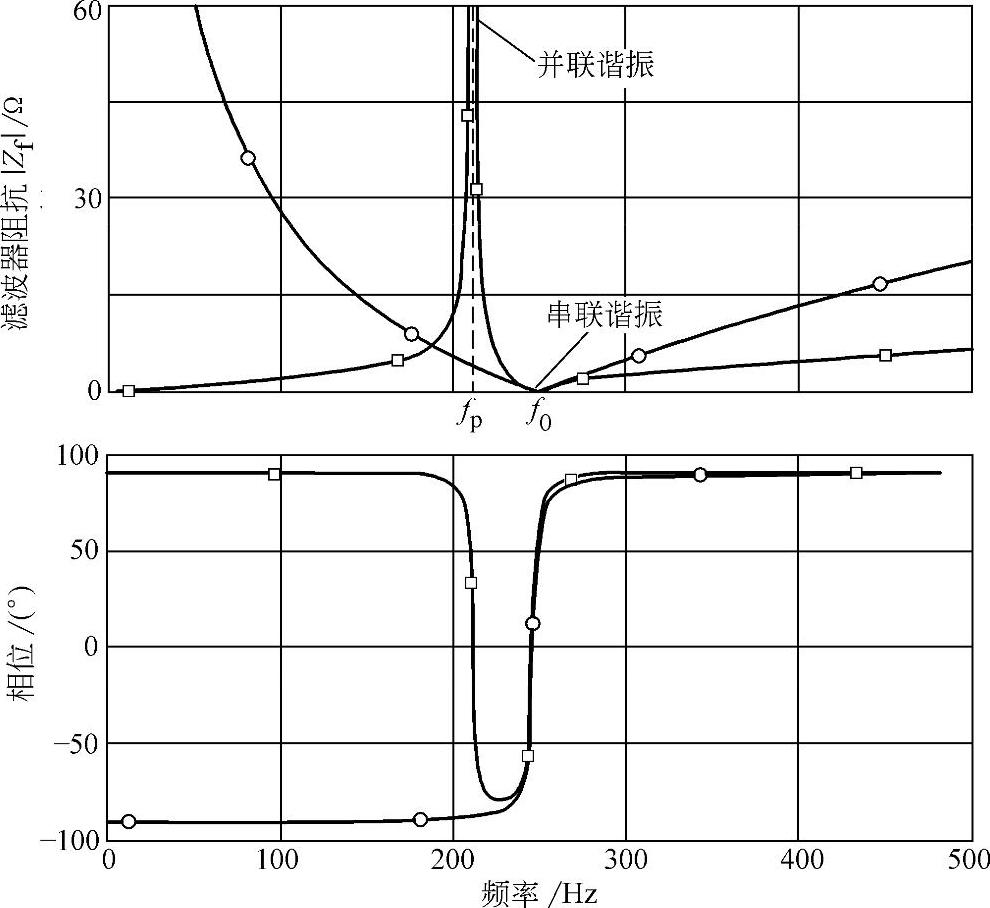
图4-17 单调谐滤波器阻抗和相位频率特性

注：图中标注□的曲线对应考虑接入点短路阻抗为1Ω时的系统综合频率特性；标注○曲线对应接入点短路阻抗无穷大，即滤波器自身的频率特性，也是参考文献[18]中通常给出的特性曲线。

这种方法设计简单，同时得到的滤波器安装容量小、效益高、损耗小，比起前述的分流式单调谐滤波器可靠性高，通常用于变压器二次母线上。但该方法与前述IEEE推荐的低于特征频率3%～15%的调谐频率仍有较大的差别，下面根据上述方法对滤波器进行设计。

由于实际工业系统中往往含有多次谐波，所以针对主要的谐波分量利用多个单调谐滤波器并联使用来分别削减相应的谐波含量是一个广泛应用的实践。比如假定增加一个7次谐波滤波器，并且让其谐振于n=6.7次（δ/2=0.043）。假定电容取18μF，则根据式（4-21）电感为

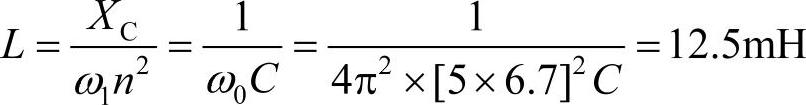
同样，考虑到取电抗器的品质因数为60，得到R=0.458，由于电容的损耗较小，这里忽略不计。得到下述并联的由5次和7次单调谐滤波器组成的滤波器组。假定滤波器接入点系统电压为10kV，短路容量为100MVA，则短路阻抗为1Ω，在忽略电阻分量条件下，相应的电感为3.18mH。得到图4-18所示的仿真电路，其中I_s是扫频电流源。

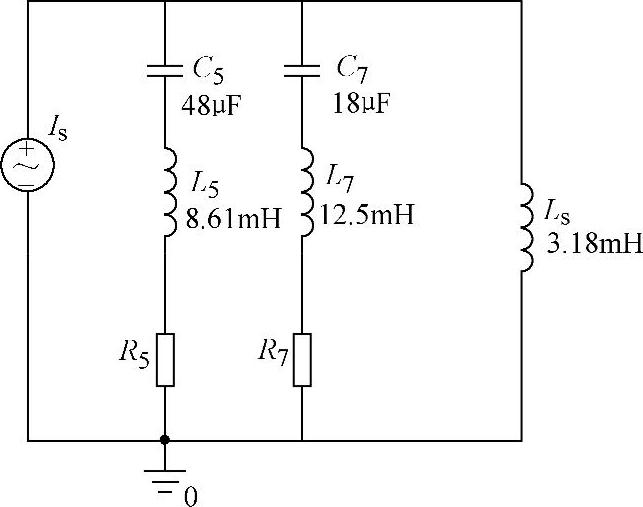
图4-18 PSPICE中的仿真电路

图4-19所示为仿真得到的5、7次单调谐滤波器组频率特性，标注○的曲线为不考虑系统短路阻抗时的滤波器频率特性，标注□的曲线为短路阻抗为1Ω时的系统综合频率特性。

当增加5、7次滤波器后，如果系统中存在的其他次谐波仍然超标，则往往需要进一步增加相应的滤波器。应当指出的是，每个单调谐滤波器均会引起谐振频率向低于其调谐频率的方向移动，假如被移动后的谐振频率与某次特征、非特征和3的倍数次谐波吻合，则会导致在上述频率处出现谐波电流放大。此外，变压器的开关涌流中富含3次和偶次谐波，这也会导致对注入系统和滤波器的谐波电流的增加。

2.双调谐滤波器设计

双调谐滤波器如图4-20b所示，通常由一个串联滤波器和一个并联滤波器组合而成，它同时吸收两个频率的谐波。与图4-20a所示的相同频率的由两个单调谐滤波器构成的单调谐滤波器组相比，电路得到了简化，基频损耗较小，同时由于只有一个电抗器L₁承受全部冲击电压，而L₂的耐压可以大幅度降低，从而降低了造价。但这种滤波器结构比较复杂，调谐也较困难，然而由于占地面积小，特别是在高压大容量滤波器中应用，还是具有一定的技术和经济上的优势。

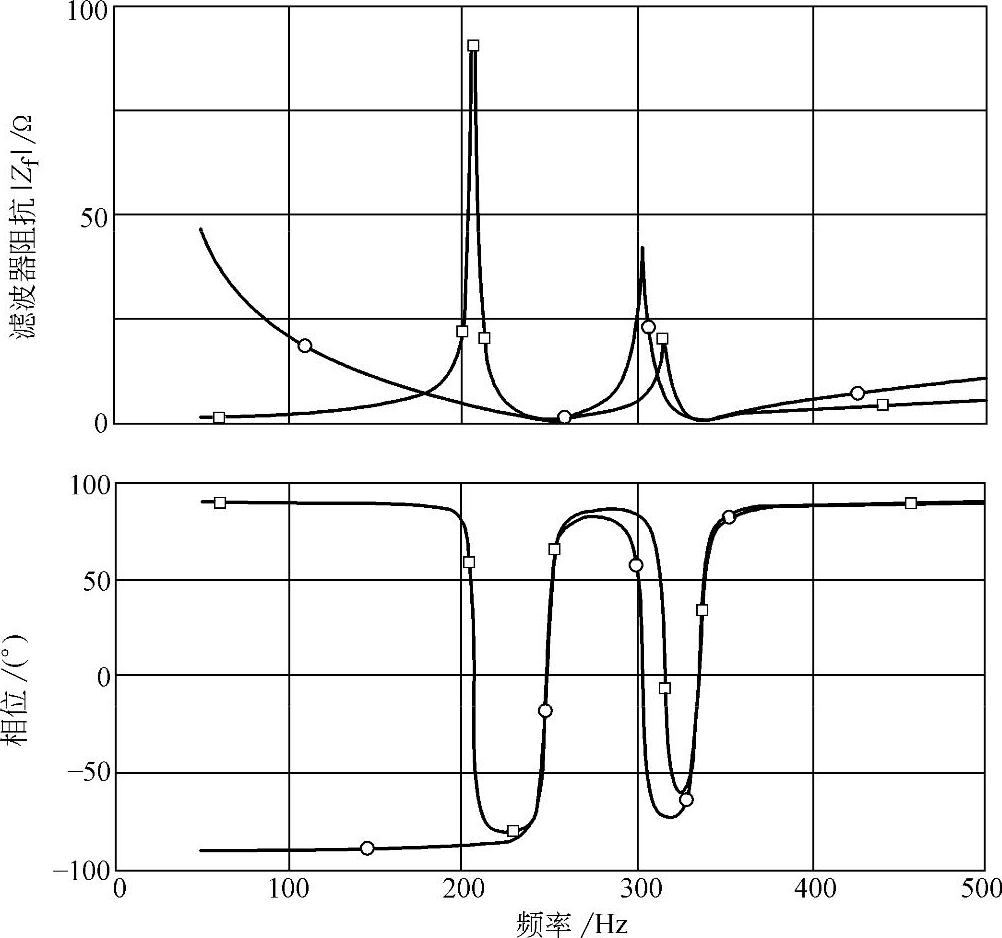
图4-19 5、7次单调谐滤波器组频率特性

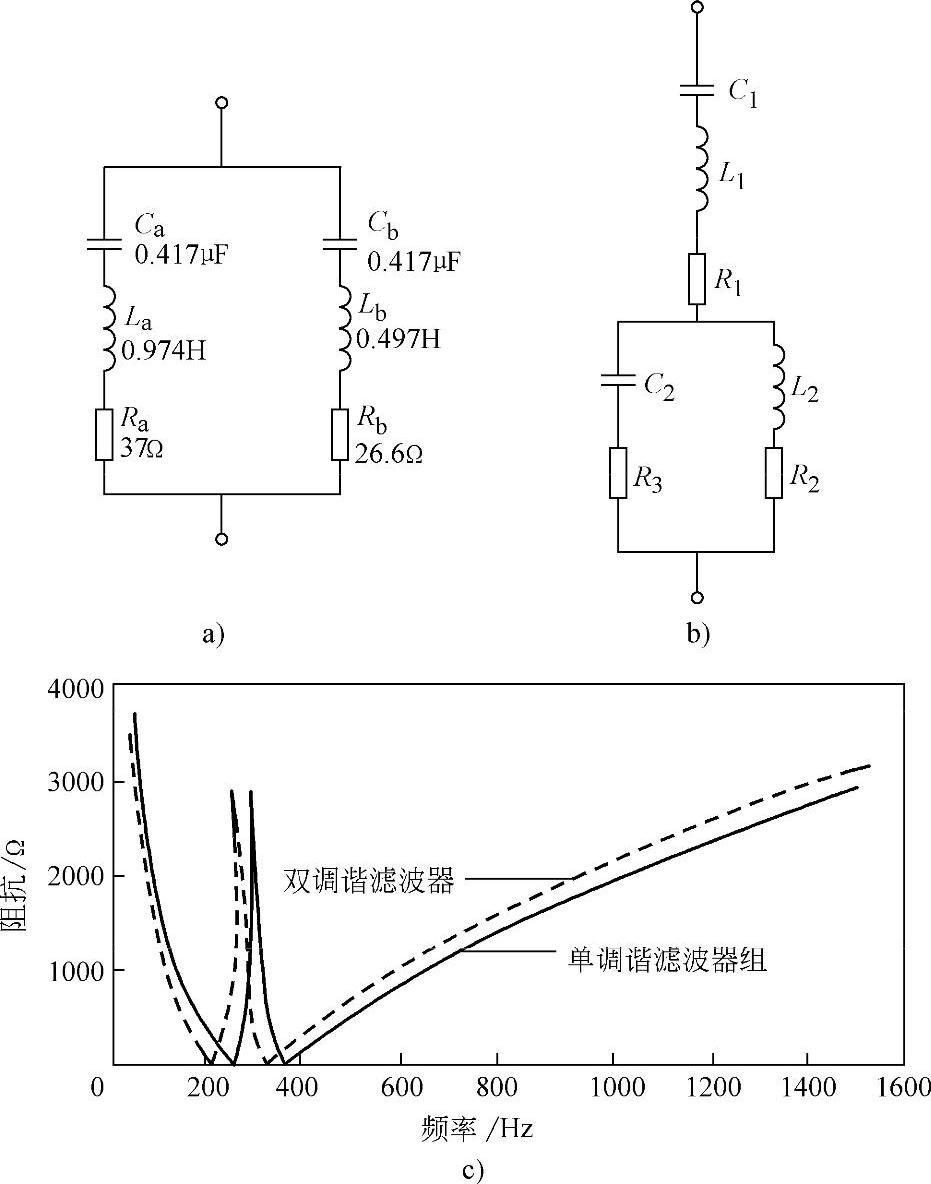
图4-20 双调谐滤波器及频谱特性

a）两个单调谐滤波器构成的单调谐滤波器组 b）双调谐滤波器 c）频谱特性(https://www.xing528.com)

由于单调谐滤波器在工程上已经有广泛的应用，而且有成熟的设计方法，所以对双调谐滤波器设计时，可以首先按常规的方法设计两个单调谐滤波器，然后再根据阻抗频率特性等效性原理，将设计参数转换成具有相同阻抗频率特性的双调谐滤波器参数，即令两个滤波器阻抗表达式中的分子和分母的系数分别相等，就可以直接利用两个不同频率单调谐滤波器的设计结果计算新滤波器的参数，此时有

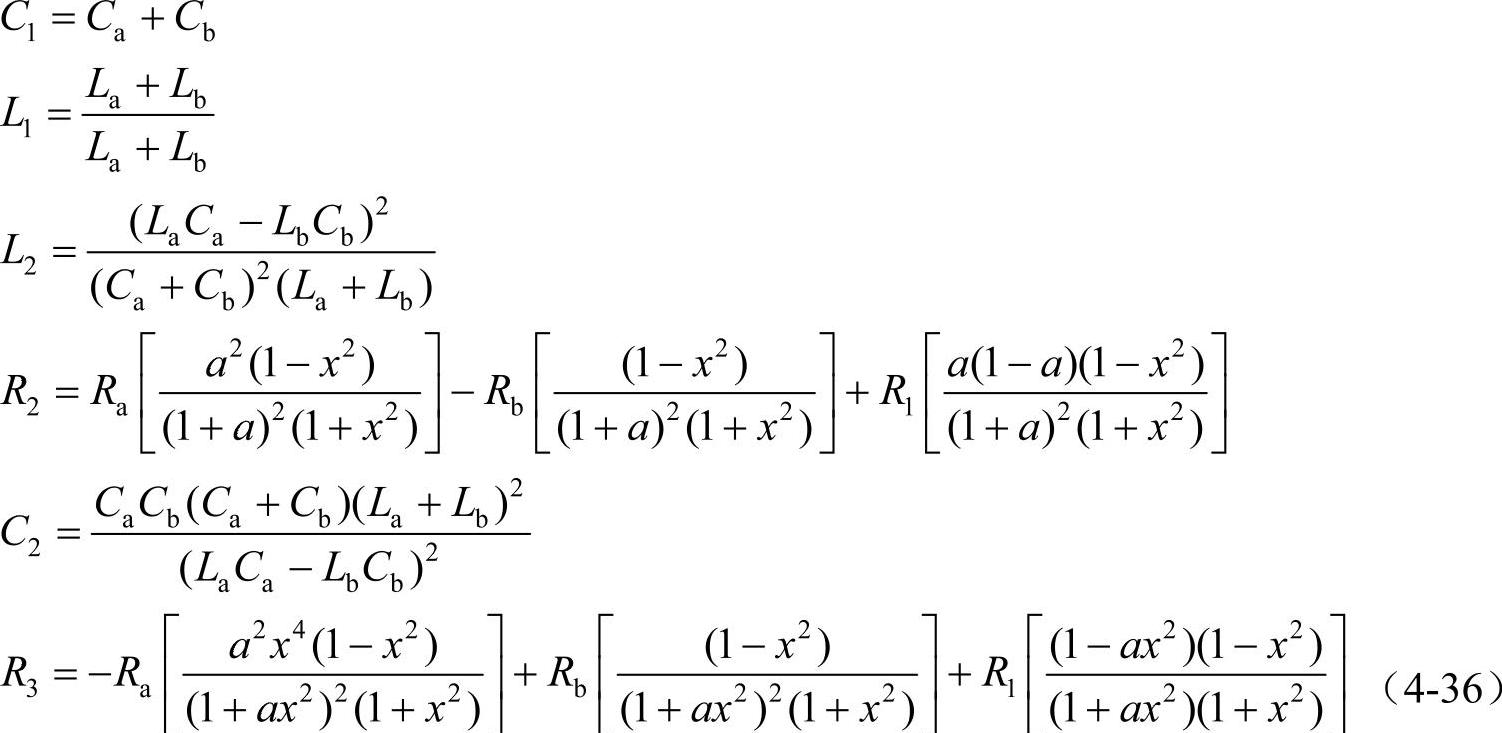
式中，a=C_a/C_b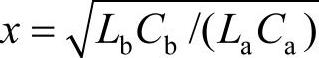；，并且通常R₁可以忽略。由图4-20a得到的双调谐滤波器参数为：C₁=0.34μF，L₁=0.329H，R₁=2.07Ω；C₂=7.931μF，L₂=0.039H，R₂=1.527Ω，R₃=1.232Ω。

两个滤波器的频谱特性如图4-20c所示，非常接近。上述方法同样可以利用到多调谐滤波器，如三调谐滤波器的设计中。随着高压、超高压交直流输电技术的应用，采用多调谐滤波器解决输电系统谐波污染和提供其所需的无功是目前国际上得到普遍使用的重要手段之一。

3.高通滤波器设计

高通滤波器[也称阻尼滤波器（DampedFilter）]如图4-21所示，主要有一阶、二阶和三阶阻尼型和C型四种。其中，一阶阻尼（减幅）型由于基频损耗过大，并且需要很大的电容，所以一般在电力滤波器中很少采用。三阶阻尼型由于C₂（比C₁容量小得多）的存在，加大了滤波器的阻抗，故基频损耗小于二阶阻尼型，但频率特性不如二阶阻尼型，所以也很少应用。而二阶阻尼型滤波器由于基频损耗小、结构简单，同时阻抗频率特性也较好，故在工程上，特别是在高频复合滤波器中得到最广泛的应用。

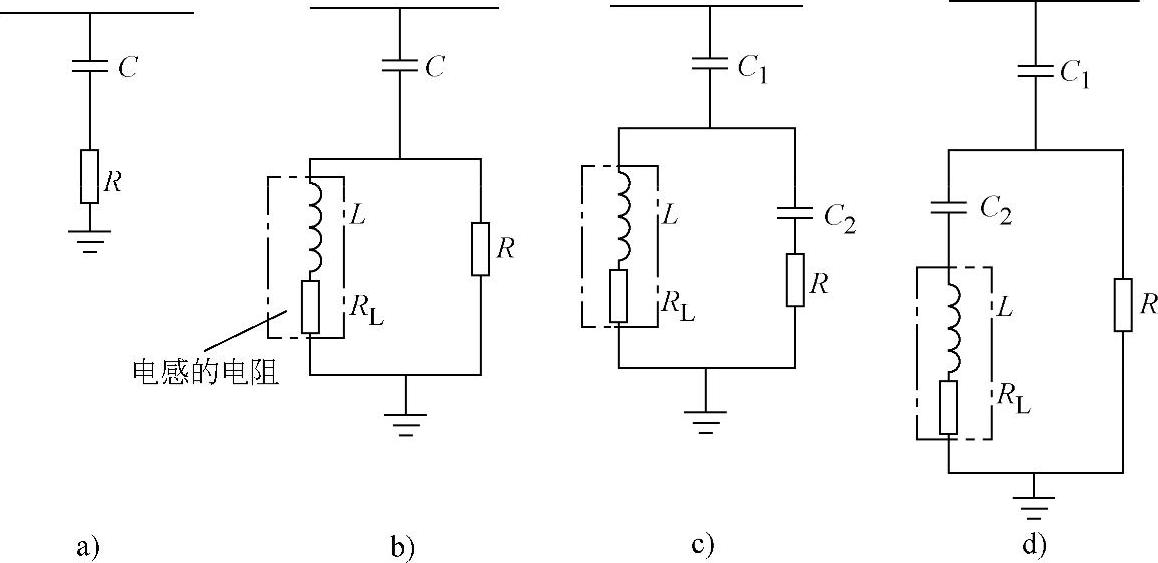
图4-21 高通（阻尼）滤波器电路

a）一阶 b）二阶 c）三阶 d）C型

高通滤波器的一个主要特点是对于参数的变化不敏感，而其性能通常可以利用下列m和截止频率f₀两个参数加以描述：

其导纳可以用下式给出：

Y_f=G_f+jB_f （4-39）

式中，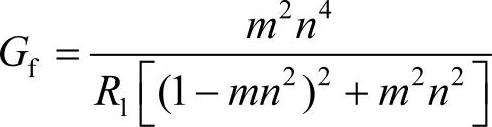

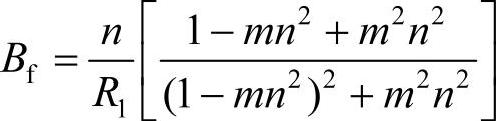
其中，n=f/f₀。

滤波器在截止频率f₀以上时，由于容抗减小，其阻抗为与并联电阻数量级相同的低阻抗，且截止频率一般略高于装设单调谐滤波器的最高特征谐波频率。而在截止频率f₀以下的频率范围，由于容抗迅速增加，使滤波器呈现容性高阻状态。对于给定的电容容量，选择截止频率f₀和参数m，以使滤波器在给定的频率范围内具有足够小的阻抗。其中，m的取值范围通常在0.5～2之间。

在忽略电感的电阻条件下，滤波器的阻抗可以表示为

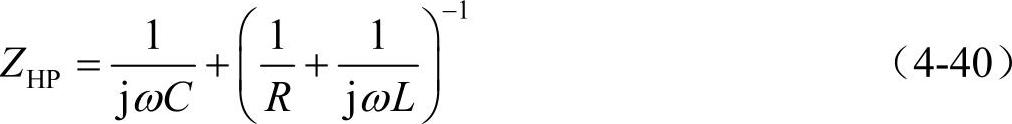
二阶高通滤波器由于电感L与电阻R并联，所以其并联阻抗不会超过电阻值，由于电阻越大，其对电抗的旁路效果越小，即滤波器特性越接近单调谐滤波器，谐振特性越陡。为了便于讨论，定义高通滤波器的品质因数为

式中，n₀为以工频ω₁为基准得到的特征谐波的次数，n₀=ω₀/ω₁。

实际设计中，有两种常用的设计方法。

第一种设计方法，是按照单调谐滤波器的公式计算滤波器的特征谐波频率^[18]，即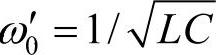，此时品质因数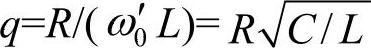的取值范围为1～5，为国内冶金企业所推荐使用。

第二种设计方法，是将前述截止频率f₀作为调谐频率，对应的截止谐波次数n₀=X_C1/R。因为此时q=R/（ωL）是频率的函数，为了使品质因数仍为一个确定的数，通常和单调谐滤波器一样，定义滤波器容抗和感抗相等的频率，即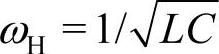时的q值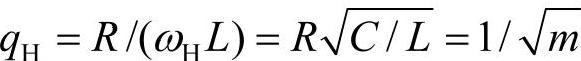，其中m的取值范围为0.5～2（q=1.414～0.707），被IEEE和电力系统所推荐。这种方法设计的滤波器基波损耗不大，因为基波电流主要流经电感L，高频损耗为主要的，因此在满足滤波要求条件下，截止谐波次数n₀不宜取太小，容量也不宜过小。

实际上，两种设计方法虽然对滤波器的调谐频率的定义不同，但对品质因数的定义却是相同的，即均定义在滤波器的感抗和容抗相等时。为了便于比较，根据截止频率为ω₀=1/（CR）和第一种设计方法的调谐频率ω₀′，得到

根据式（4-41）上式可改写为

即两种设计方法得到的滤波器的调谐频率之比是品质因数q的倒数或参数m的平方根。当q=1或m=1时，两种设计方法得到的滤波器参数相同。

尽管无源滤波器在电力系统中得到广泛的应用，但其本身存在下述问题：

1）无源滤波器由于其调谐频率和容量均是固定的，不能适应系统参数和运行条件的变化，而元件的老化、变质和温度影响均可能导致滤波器失谐，甚至引起谐波放大。

2）滤波器的设计受到系统阻抗的影响，对于需要无功补偿容量很大的场合，滤波器的投入可能会导致系统过补偿和过电压，而其切除又可能引起欠电压。特别是无源滤波器作为一个分流装置，必须在滤波器的阻抗远低于系统阻抗时才能有效发挥作用，因此对于短路容量大的系统其作用有限。

3）由于单调谐滤波器只能消除特定的某次谐波，实际系统中往往由于谐波含量丰富而需要多组滤波器并联。此时由于滤波器之间的相互影响会改变单个滤波器的调谐特性，而其中一组滤波器的切除会改变整个系统的频谱特性和谐波电流的走向，以致造成剩余滤波器组的过负荷或损坏。

4）滤波器和系统之间或滤波器组间可能会产生并联谐振，从而导致对特征或非特征谐波电流的放大。高通滤波器虽然不会引起谐波放大，但其滤波效率较低，并且体积较大。

5）对于大容量滤波器而言，其串联电阻可能产生可观的有功损耗。

随着电力电子技术的发展，有源滤波器由于采用谐波对消原理，故可以有效地同时消除多次谐波，并且不会出现谐波放大的问题，所以得到越来越广泛的关注与应用。