什么是谐波？谐波含量和间谐波解析

1822年，法国数学家傅里叶（J.Fourier，1768—1830）指出，一个任意函数都可以分解为无穷多个不同频率正弦信号的和。据此，IEEE定义“谐波是周期性波形或周期量的正弦分量，其频率为基频的整数倍”。谐波次数n为“以谐波频率和基波频率之比表示的整数”。目前一个普遍接受的谐波定义为：“谐波是一个周期电气量的正弦波分量，其频率为基波频率的整数倍”。

理想电力系统所提供的电压和电流具有工频正弦波形。以电压为例，可表示为

式中，U为电压有效值；θ为初相角；ω为角频率，ω=2πf=2π/T；f为频率；T为周期。

当正弦波电压作用在无源线性元件（如电阻、电感和电容）上时，所产生的电流和电压仍为同频率的正弦波。但是当正弦波电压施加在非线性负荷上时，电流就成为非正弦波。对于周期为T的非正弦信号u（ωt），在满足狄里赫利条件下，可分解为如下形式的傅里叶级数：

式中

即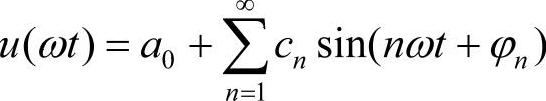 （4-3）

式中，c_n、φ_n和a_n、b_n的关系为

其中，频率分量与工频相同的分量称为基波（n=1），频率为基波频率其他整数倍的分量称为谐波，谐波次数为谐波频率和基波频率的整数倍。与之相关的定义包括：

谐波含量（Harmonic Content），指的是从周期性交流量中减去基波分量后所得到的量。其中，谐波电压含量U_H定义为

谐波电流含量I_H定义为

谐波含有率以HR（Harmonic Ratio）表示周期交流量中含有的n次谐波分量的方均根值与基波分量的方均根值之比的百分数。比如第n次谐波电压的含有率表示为

式中，U_n为第n次谐波电压有效值（方均根值）；U₁为基波电压有效值。(www.xing528.com)

并定义电压谐波总畸变率THD_u（Total Harmonic Distortion），即谐波含量的方均根值与基频分量的方均根值之比的百分数，为

而电流谐波总畸变率THD_i为

我国电力系统的基波频率为50Hz，因此2次谐波为100Hz（或120Hz），3次谐波为150Hz（或180Hz）。在某些暂态现象中，电力系统会出现一些非整数的分数次谐波，如间谐波、次谐波和分数谐波等。作为谐波的一种，间谐波可能出现在各个等级电压的网络中。它们可以以离散频率或者很宽的频谱的形式出现。间谐波波形畸变的主要来源是静态变频器、周波变频器、异步电动机和电弧装置。电力线载波信号也可以被认为是一种间谐波。

间谐波的影响还没有被广为认知，但是已经表现出影响电力线载波信号，并且会给显示设备（比如CRT）带来视觉上的闪烁。

这里有两个常用的定义值得注意：

1）IEC标准中对总谐波电流的方均根值定义，仅限于40次及以下的谐波，即

2）在开关电源等电力电子装置的讨论中，功率因数通常定义为

式中，cosϕ定义为位移因子，有时也记为K_d。

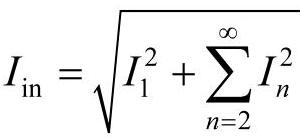畸变因数K_p，定义为输入交流电流基频分量的有效值和交流电流的有效值之比，即。其中，，得到；

因此，功率因数也可记为PF=K_dK_p。所以对于开关电源而言，当谈到功率因数时，往往包括畸变因数，即谐波失真的影响，并且通常畸变因数起着主导的作用。