3.4.1.1 不平衡的定义
IEC定义电压不平衡为多相系统中基频线电压的方均根值,或两个顺序线电压之间的相角不相等,并且将三相电压不对称(或者不平衡)定义为负序或零序分量与正序分量之比,通常用百分比来表示。实际电力系统中,负序或零序电压的产生通常是由于不平衡负荷接入系统,并且从电力系统中抽取的三相电流具有不同的幅值或相位差而引起的。理论上,正常运行的三相电动机、发电机和变流器不会引起不平衡。但可能由于设计的原因造成一些小的、可以忽略的不平衡。馈线阻抗的差异同样也会造成一定的不平衡。造成三相不平衡的一个重要原因是系统中大量存在的单相负荷,如家用电器、计算机、照明设备、加热器、电气化铁路、焊机等。在实践中,这些设备应当尽可能均匀地接入三相系统,以减少不平衡。但特殊的三相设备(如交流电弧炉),由于三相电极的独立性,实际中运行中相当于三个单相负荷,从而同样会造成严重的三相不平衡。除了负荷不平衡的原因外,三相不对称故障同样会引起电压的不平衡。
图3-51给出某靠近电气化铁路的工厂三相电压呈现的明显不平衡,图3-52给出某一住宅馈线上测量得到的由于中线故障引起的持续电压不平衡的例子。
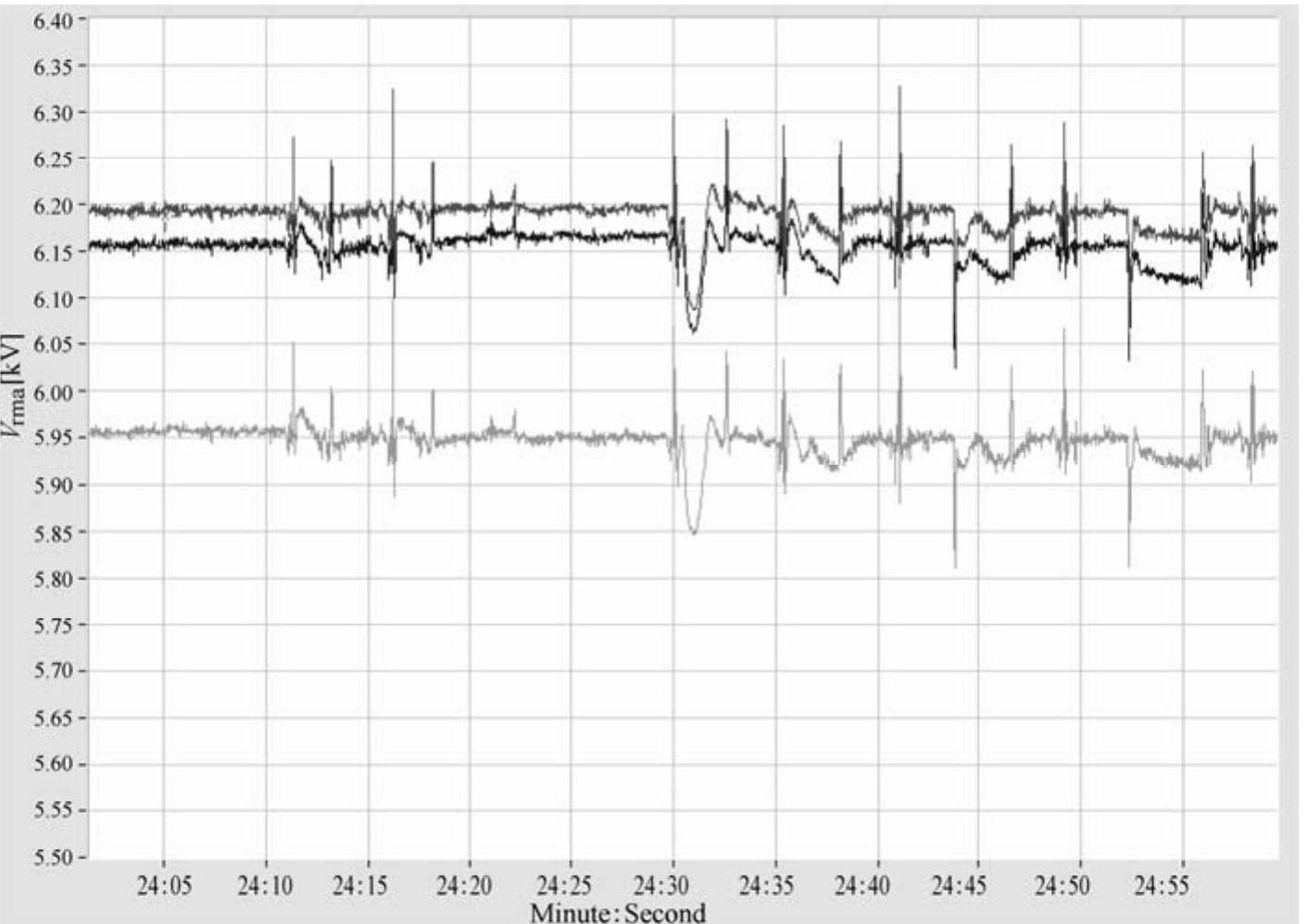
图3-51 某工厂由于电气化铁路引起的三相电压不平衡
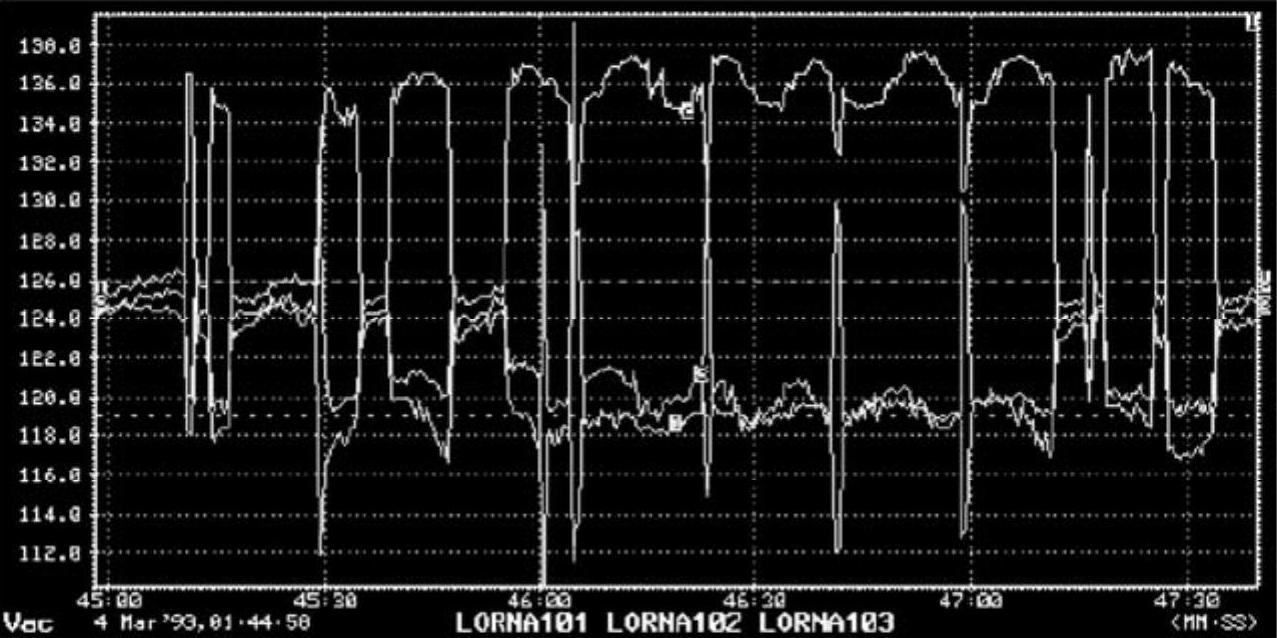
图3-52 住宅小区三相电压不平衡
根据电工理论,多相系统可以分为对称的和不对称的两大类。所谓对称的M相系统是指各相电量(电动势、电压或电流)的幅值大小相等,而且彼此之间的相移均等于(2π/M)。电力系统分析中,所谓的多相系统实际上指的都是三相系统。应当注意的是,实践中所谓三相平衡设备通常并不是指三相电流平衡,而往往指的是三相额定电流模块的差别小于20%的设备。
不平衡度可以用三相电压(或电流)中偏离三相电压(或者电流)平均值的最大量,除以三相电压(或电流)的平均值来计算,通常用百分比来表示。
电压不平衡度=100×(偏离平均电压最大量)/平均电压 (3-32)
国标中规定电力系统公共连接点正常电压不平衡度允许值为2%,短时不得超过4%。接于公共接点的每个用户,引起该点正常电压不平衡度允许值一般为1.3%。
例如,以图3-51为例,相电压稳态幅值分别为6.20kV、6.15kV和6.05kV,平均值为6.133kV。三个读数中距平均电压的最大偏移是0.083kV。不平衡度为100%×0.083/6.133=1.35%。而以图3-52为例,在47min附近的平稳区间中,三相电压分别为约119V、119V、136V,得到的不平衡度为9.09%。
又如电弧炉在熔化期其平均负序电流可以高达额定电流的20%,而其峰值则达到额定电流的40%。图3-53为额定电流944A的电弧炉的负序电流波动。其峰值大体达到约400A。
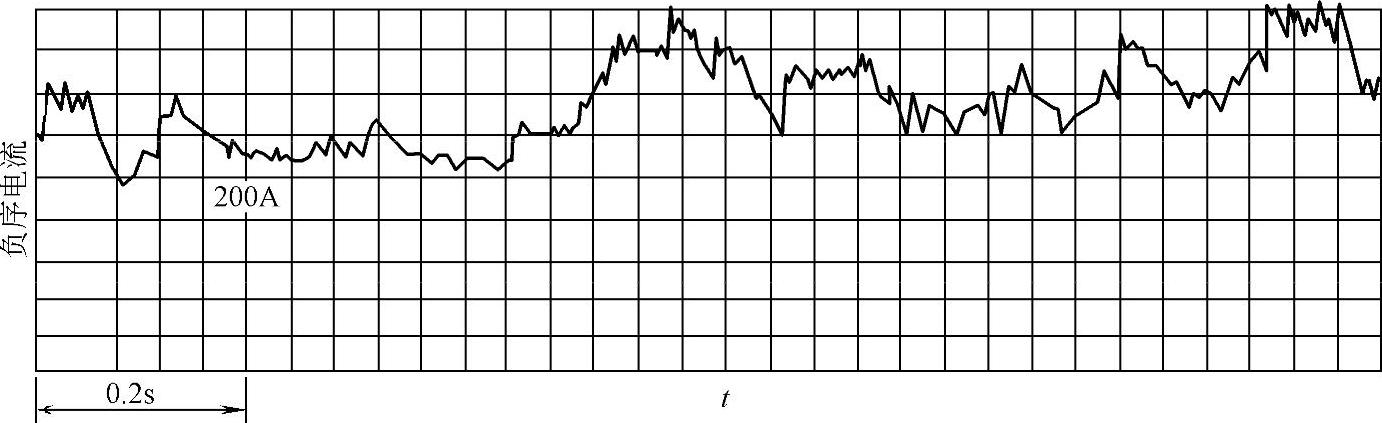
图3-53 电弧炉22kV馈线的负序电流
3.4.1.2 电压不平衡的影响
当不平衡电压加于三相电动机时,相电压的不平衡使得电动机中的负序电流增加,产生与电动机旋转方向相反的旋转磁场和反向转矩,从而降低了效率的同时增加了转子内的热损失和振动噪声,当一相开路,转子处于单相运行时,情况最为严重。资料指出,电压不平衡度为2.8%时,异步电动机的温度达到正常运行时允许的最大值。为了保证电动机的寿命,日本电气学会提出应将电压不平衡度限制在1%以下。表3-7列出了U型与T型机座两种电动机在规定的三相不平衡电压时的温升增高表。
表3-7 相电压不平衡对异步电动机温升的影响

所有的电动机对相电压不平衡均是敏感的,而对密封的空压机电动机的影响要比对标准的空气冷却电动机的影响更大。由表3-7可以看出,当相电压不平衡超过2%时,若电动机接近满负荷运行,就很可能产生过热。
某些电子设备如计算机,在相电压不平衡大于2%或2.5%时,也可能受到影响。通常,不应将单相负荷接在有对相电压不平衡敏感的设备的三相供电回路中。这种设备应分开供电。
大多数电力公司采用三相四线制 联结、中性点接地的配电系统,以便单相变压器能够连接于相线与中性线之间,向居民住宅及街灯等单相负荷供电。单相负荷的变化引起三相线路中电流各不相同,因而产生的电压降也不相同,并使得相电压不平衡。一般最大不平衡的相电压出现在一次配电系统的末端,实际不平衡程度则取决于如何将单相负荷平均分配在系统各相之间。对于此类单相供电方式而言,完全平衡是根本做不到的,因为负荷是在不断变化,所以相电压的不平衡度也在不断变化。电力公司的任务就是适当地在分支线路和馈电线两方面平衡三相中的单相负荷,使负荷的不平衡及相应的相电压的不平衡保持在适当的范围内。
联结、中性点接地的配电系统,以便单相变压器能够连接于相线与中性线之间,向居民住宅及街灯等单相负荷供电。单相负荷的变化引起三相线路中电流各不相同,因而产生的电压降也不相同,并使得相电压不平衡。一般最大不平衡的相电压出现在一次配电系统的末端,实际不平衡程度则取决于如何将单相负荷平均分配在系统各相之间。对于此类单相供电方式而言,完全平衡是根本做不到的,因为负荷是在不断变化,所以相电压的不平衡度也在不断变化。电力公司的任务就是适当地在分支线路和馈电线两方面平衡三相中的单相负荷,使负荷的不平衡及相应的相电压的不平衡保持在适当的范围内。
3.4.1.3 不平衡分析与计算
1.对称分量法
从电工原理知道,任何不对称的三相相量均可用对称分量法分解为三组对称的正序、负序和零序分量。正序、负序、零序分量的概念及计算方法是在1918年,由C.L.Fortescue在美国电气工程师学会的一次会议上提出的,该方法已广泛用于分析电力系统的不对称运行及故障分析。对称分量法的基本概念是,电力系统在理想条件下工作时,A、B、C三相电压均为50Hz的正弦电压且有效值相等,B相电压相位落后A相120°(2π/3),C相落后B相120°,即

满足上述条件的三相电压为正序电压。同理,如果三相负荷相同,则此时三相电流也满足上述关系,即三相电流为50Hz的正弦电流且有效值相等,B相电流相位落后A相120°(2π/3),C相落后B相120°。如果令 ,则可以定义基频正序算子
,则可以定义基频正序算子
e1=(1,α,α2) (3-34)
可将上述理想三相电压表示成三维相量的形式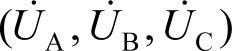 ,则上面的三相正序电压可以表示成
,则上面的三相正序电压可以表示成

当电力系统出现故障或负荷不平衡情况,虽然三相电压或电流仍然是50Hz的正弦波,但有效值和相位将不再满足上述关系,为了便于分析,人为定义了电力系统中的负序量和零序量。即如果三相电量的相量 、
、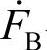 、
、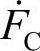 满足A、B、C三相有效值相等,且B相领先A相120°,C相领先B相120°,则称为其为三相负序相量;如果三相电量的相量F
满足A、B、C三相有效值相等,且B相领先A相120°,C相领先B相120°,则称为其为三相负序相量;如果三相电量的相量F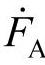 、
、 、
、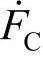 满足:A、B、C三相的有效值与相位均相等,则称其为三相零序相量。可以仿式(3-34)分别定义为
满足:A、B、C三相的有效值与相位均相等,则称其为三相零序相量。可以仿式(3-34)分别定义为
基频负序算子:
e2=(1,α2,α) (3-36)
基频零序算子:
e0=(1,1,1) (3-37)
很明显,e1、e2、e0是三维空间线性独立的相量,因此可以构成三维相量空间的基。对于三维相量空间中的任意相量,可以用它线性表出,见图3-54,定义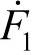 为正序分量,
为正序分量, 负序分量,
负序分量,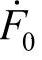 零序分量:
零序分量:

很明显,如果已知系统三相电压相量,采用公式(3-38)可以计算出正序电压相量、负序电压相量和零序电压相量分量

式(3-39)表明,由三个不对称相量可以分解为唯一的三组对称相量,其中负序电压为

据此可以定义电压不平衡度为负序电压的方均根值与正序电压方均根值之比,即
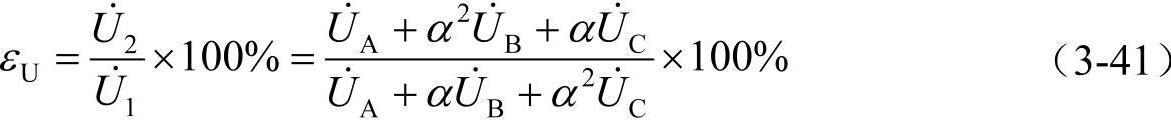
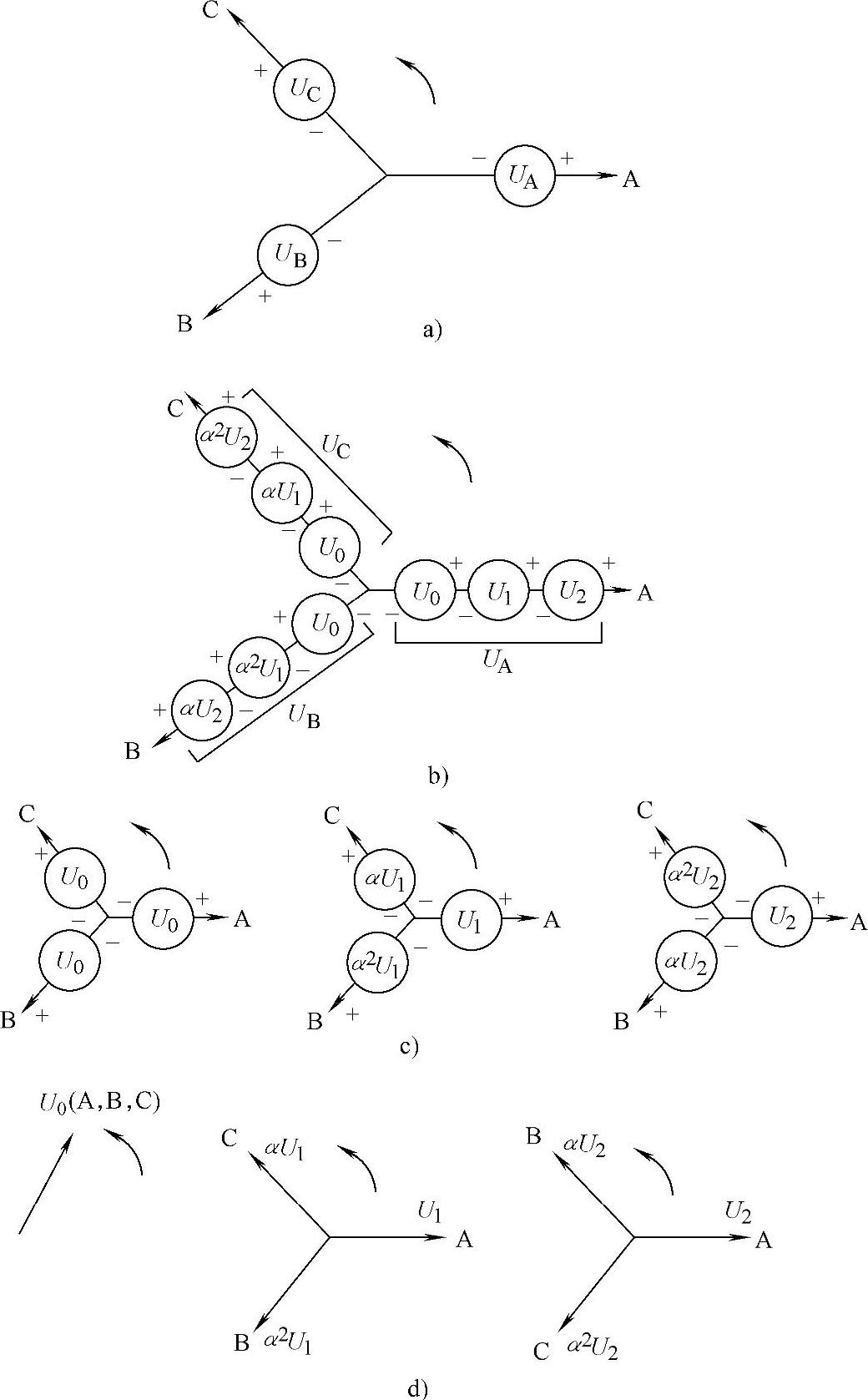
图3-54 三相不对称电压的分解过程
同样,电流的不平衡度定义为负序电流的方均根值与正序电流方均根值之比。在各相电流的幅值和相位均已知的条件下,IEC建议可以用下式去计算负序电流:
1)三相负荷星形联结
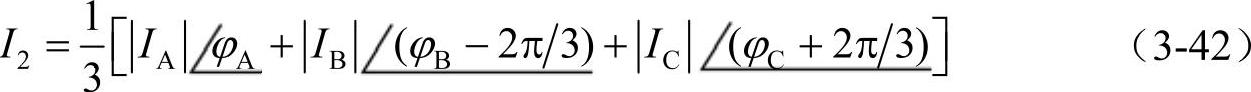
2)三相负荷三角形联结

3)接于相间的单相负荷

利用上述电流的计算可以得到相对负序电压的一个计算公式:

式中,Isc为企业内公共连接点的三相短路电流。
图3-55给出了一个典型的三相不对称电压利用对称分量法分解的结果。
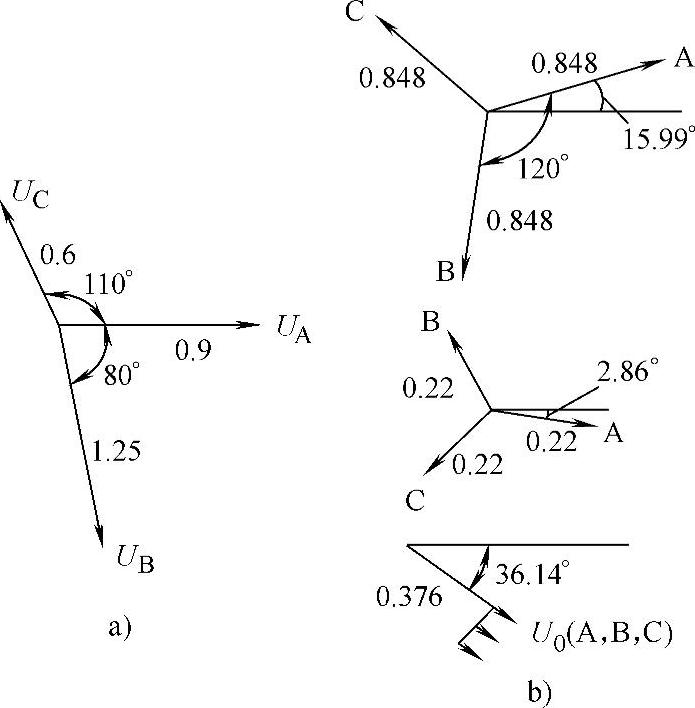
图3-55 典型的三相不对称电压利用对称分量法分解的结果
a)不对称三相电压 b)对称分量法分解(由上至下:正序,负序,零序)
例中不平衡度为

国标中规定在已知三个相量 、
、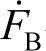 、
、 时,不平衡度可以用下式得到
时,不平衡度可以用下式得到

式中,L为参变量,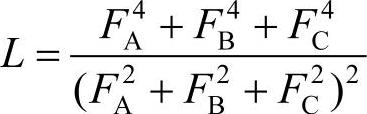 。
。
式(3-46)可以改写为

式中,D为参变量

国标中还另外给出了不平衡度的两个近似计算公式:
如公共连接点的正序阻抗与负序阻抗相等,则

式中,I2为电流的负序分量(A);SK为公共连接点的三相短路容量(MVA);UL为线电压(kV)。
相间单相负荷引起的电压不平衡度为

式中,SL为单相负荷的容量。
电气化铁路是一种典型的单相负荷(见图3-56),以SS8电力机车为例,其牵引功率为4.8MW,假定功率因数为0.8;则视在功率为6MVA。假定将变电所看作一个独立用户,按国标独立负荷1.3%的负序允许值的要求,则可以接入短路容量为460MVA的系统之中。但注意到由于通常一个变电所可能向多台,比如5台电力机车供电,此时就可能要求系统短路容量达到2300MVA,否则就可能超出国标要求。
但是应当指出,由于上述讨论是基于稳态相量的,其计算基于工频周期,因此并不适用于动态变化的系统。
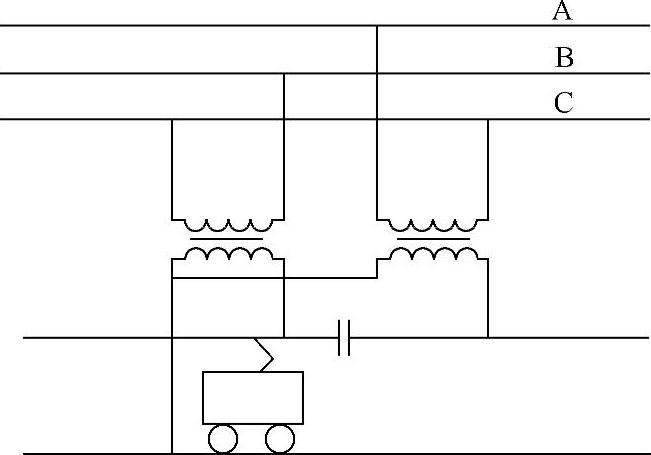
图3-56 采用单相变压器的电气化铁路接线图
2.瞬时值分析
随着计算机技术和FACTS技术的发展,快速控制成为现代电力系统控制的一个基本要求。各种基于瞬时值,如瞬时无功等,而不是方均根值的控制方法得到越来越广泛的重视和应用,因此上述基于稳态的对称分量法的适用性就成为问题。图3-57所示的系统短路时三相电流的瞬时值的剧烈变化就提出了上述算法难以解决的问题。
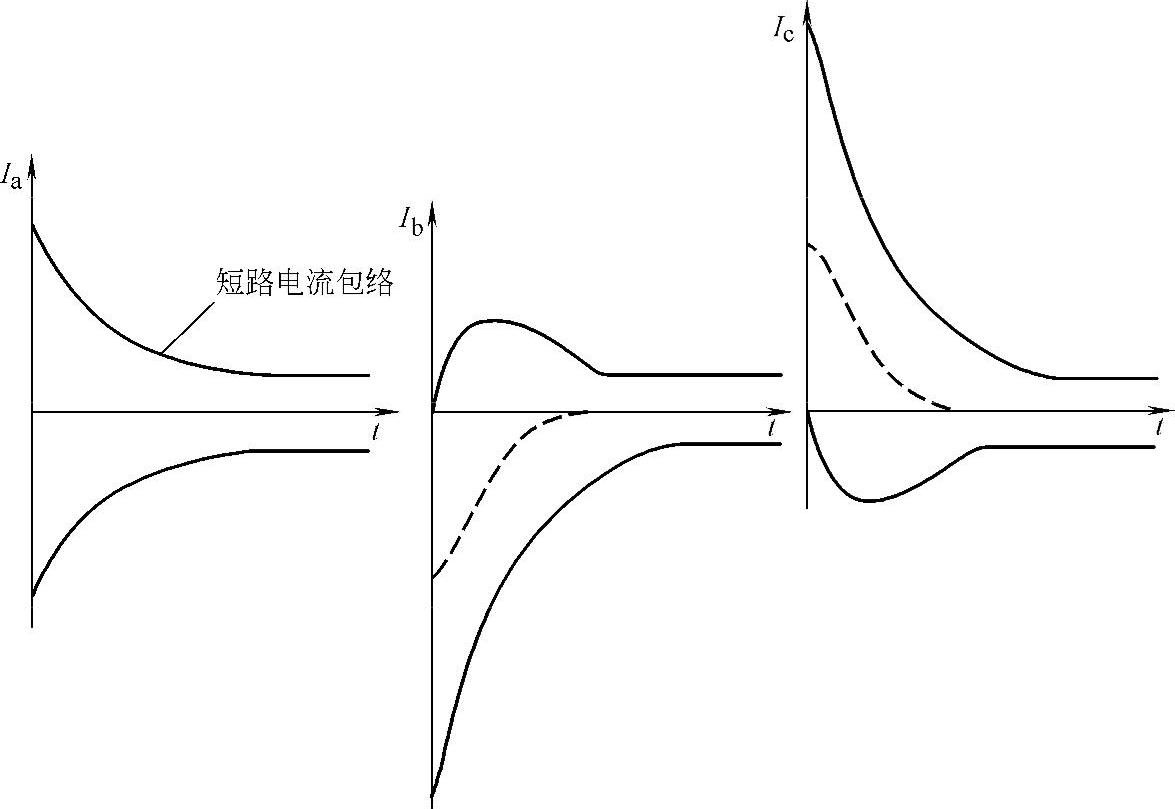
图3-57 单相短路时三相电流包络
为了便于说明,将上述稳态算子α=e-j2π/3直接用于一个三相对称系统的瞬时计算,此时三个相量利用瞬时值分别表示为

利用上述稳态变换算子可以得到

即当利用稳态算子对一个对称三相系统的瞬时值形式进行描述时,将出现一组互为共轭复数的正序和负序分量,也可以将式(3-51)表示为两个旋转方向相反的矢量图。这显然与传统对称分量法的结论不一致,故不能简单地加以直接应用。
实际上,为了快速计算系统基波电压的正序分量、负序分量和零序分量,可以利用瞬时功率理论中计算电流基波正序分量同样的方法。具体步骤如下:
1)定义基波瞬时正序分量为

经αβ变换后,得到瞬时αβ分量:

2)定义αβ0变换矩阵为
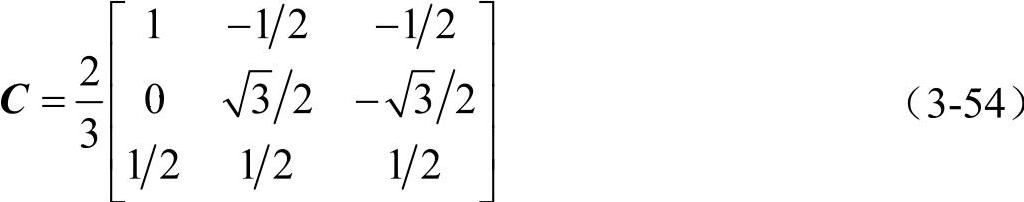
不难看出矩阵C为可逆矩阵,其逆矩阵为

对三相电压进行αβ0变换,即

定义三相电压中的零序分量为
 (https://www.xing528.com)
(https://www.xing528.com)
因此,零序电压分量(包括基波和谐波)可瞬时计算得出,称为瞬时零序电压分量。将瞬时零序电压分量分解为基波分量和其他的分量,则得到三相电压的基波零序分量。
如果三相电压中只存在基波分量,对其进行αβ0变换,得到

令
u=uα+juβ (3-59)
为αβ平面的矢量。根据分析不难看出,如果三相电压为正序基波电压,则u=uα+juβ为αβ平面上逆时针以角速度ω旋转的矢量,记为u+,在αβ平面上画出原点为圆心、半径为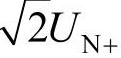 的圆(UN+为基波正序电压的有效值)。同理,如果三相电压为负序基波电压,则u=uα+juβ为αβ平面上顺时针以角速度ω旋转的矢量,记为u-,在αβ平面上画出原点为圆心、半径为
的圆(UN+为基波正序电压的有效值)。同理,如果三相电压为负序基波电压,则u=uα+juβ为αβ平面上顺时针以角速度ω旋转的矢量,记为u-,在αβ平面上画出原点为圆心、半径为 的圆(UN-为基波负序电压的有效值)。如果三相电压中既有正序分量又有负序分量,则u=uα+juβ在αβ平面上画出椭圆轨迹,为角速度ω逆时针旋转的矢量与角速度ω顺时针旋转的矢量所合成的矢量。如图3-58所示,在t和t+Δt时刻,矢量分别为u(t)、u(t+Δt),它们都可以分解为逆时针方向旋转的正序矢量和顺时针方向旋转的负序矢量之和,即
的圆(UN-为基波负序电压的有效值)。如果三相电压中既有正序分量又有负序分量,则u=uα+juβ在αβ平面上画出椭圆轨迹,为角速度ω逆时针旋转的矢量与角速度ω顺时针旋转的矢量所合成的矢量。如图3-58所示,在t和t+Δt时刻,矢量分别为u(t)、u(t+Δt),它们都可以分解为逆时针方向旋转的正序矢量和顺时针方向旋转的负序矢量之和,即

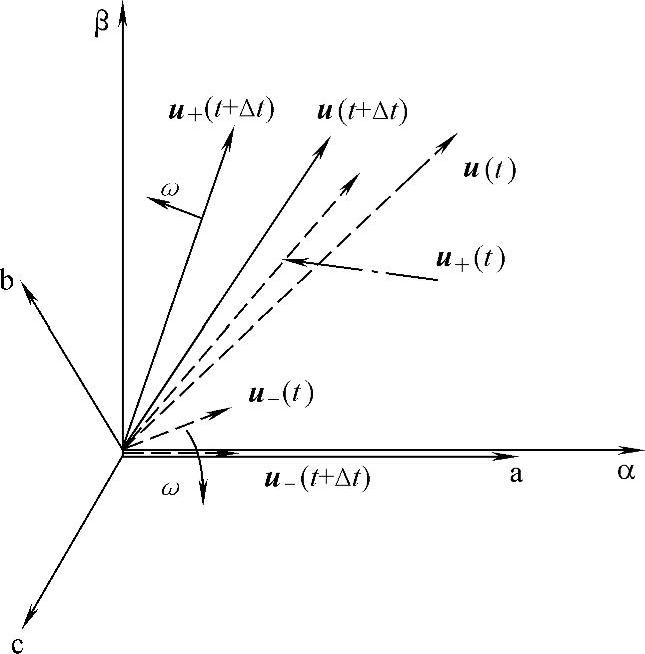
图3-58 三相电压αβ平面上的矢量图
不失一般性,令t时刻正序、负序矢量分别为

则有
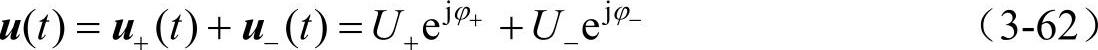
在t+Δt时刻,正序矢量大小不变(或变化为Δt的高阶无穷小量)向逆时针方向旋转+ωΔt角度,而负序矢量大小不变(或变化为Δt的高阶无穷小量)向顺时针方向旋转-ωΔt角度,即
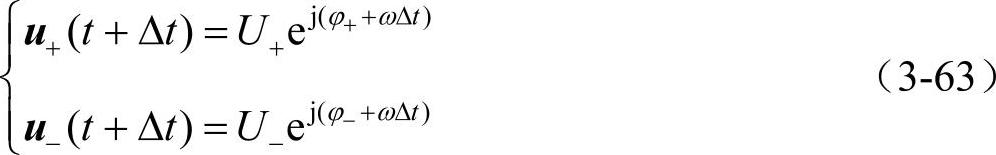
令Δt趋于无穷小,得到
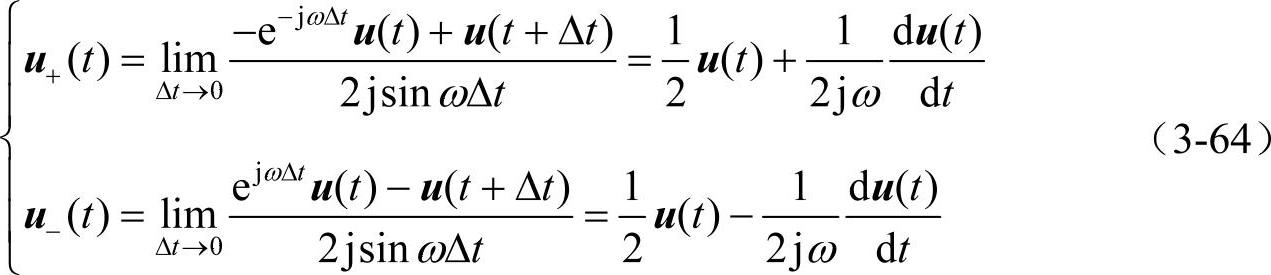
由于u(t)=uα(t)+juβ(t),因此得到:
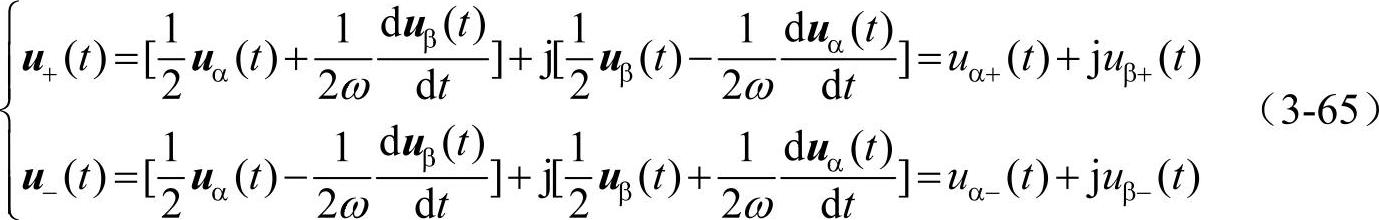
最后可以得到
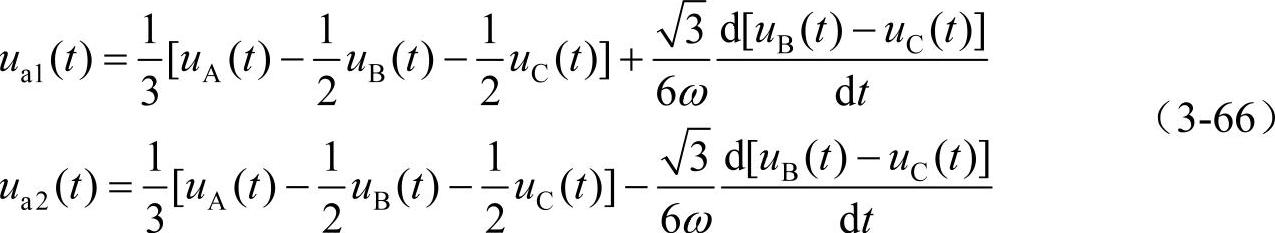
求出A相的基波正序分量、基波负序分量后,B、C相的可类似求出。因此,上述基波正序、负序、零序可以定义为三相系统基波电压的瞬时基波正序分量、负序分量和零序分量。当三相电压为基波分量时,也可以通过简单的方法从稳态算子直接求出三相基波瞬时正序、负序和零序分量,具体方法如下:
将相量换成瞬时量,而将虚数j换成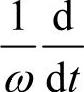 ,其中ω为基频频率,即
,其中ω为基频频率,即

此时,稳态对称分量算子α、α2改写为

代入式(3-66)得到A相电压的负序相量为
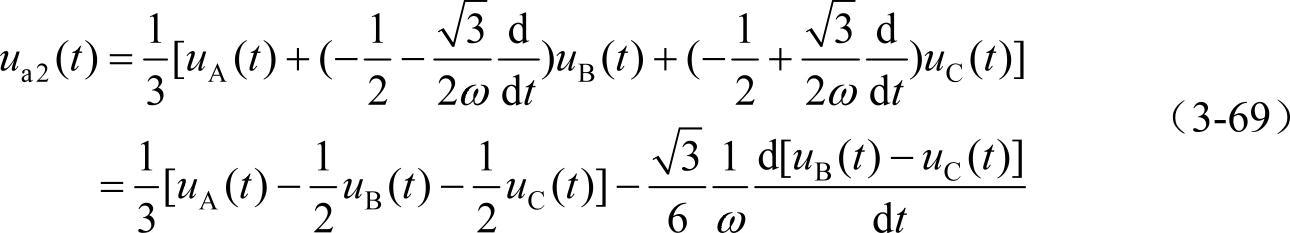
与式(3-66)相同,可以用于瞬时不对称补偿的计算之中。
3.4.1.4 不平衡补偿
供电侧的补偿措施包括可以利用对馈线换相连接的方式,使各相的阻抗相等。常规的用户侧的不平衡补偿措施包括抑制负序电流的发生量和向系统注入负序电流两种,见表3-8和3-9所示。
表3-8 用户侧电压不平衡的抑制措施

表3-9是对单相负荷电气化铁路不同变压器接法的100kVA试验设备的参数。
表3-9 单相负荷连接方法

斯坦梅茨(Steinmetz)平衡方法是目前公认的对于稳态不平衡负荷进行补偿的有效措施。平衡系统总功率是恒定的且与时间无关,而不平衡系统的总功率却是脉动的。因此将不平衡三相系统变成平衡的三相系统时,在变换设备中应该设有能够暂时储积电磁能量的电感线圈和电容器。最简单的例子是如图3-59a所示的单相电阻负荷Gab构成的三相不平衡系统。图3-59b是在其他两相分别适配电抗为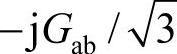 的电感和电抗为
的电感和电抗为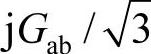 的电容,构成平衡的三相系统。
的电容,构成平衡的三相系统。

图3-59 三相平衡化电路
a)单相电阻负荷 b)平衡化三相系统
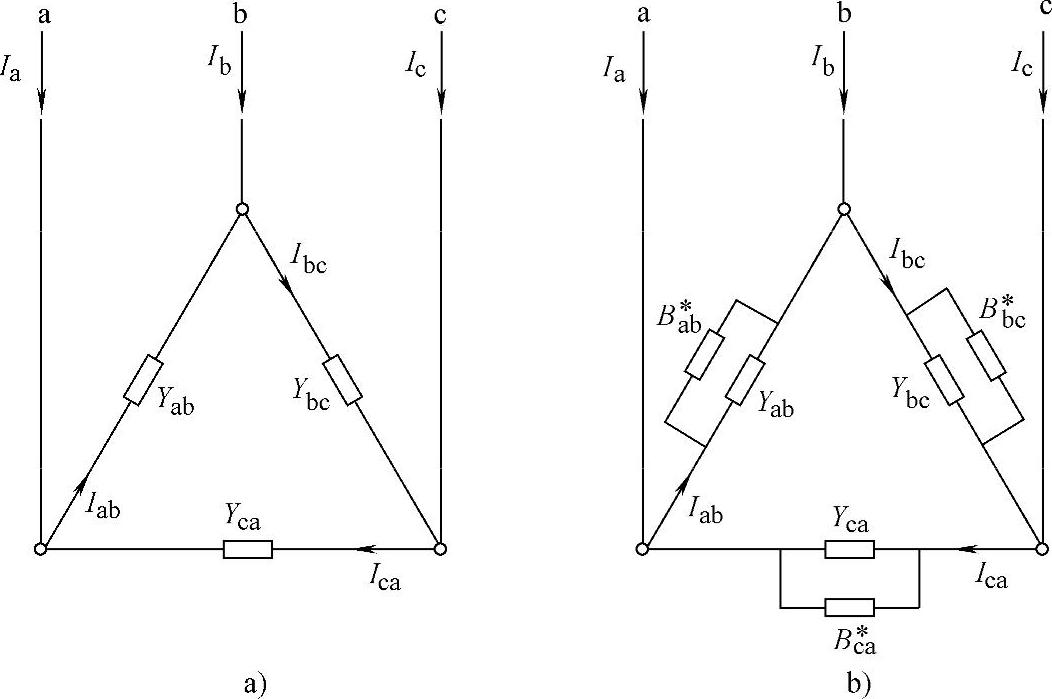
图3-60 三角形联结不平衡负荷的平衡
a)三角形联结的不平衡负荷 b)补偿后的三相负荷
该平衡的三相系统的原理图如图3-60所示。图中,电容电流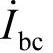 超前电压
超前电压 ,电感电流
,电感电流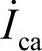 滞后电压
滞后电压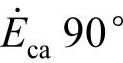 。电感和电容电流的方均根值相等,恰能构成电感和电容谐振的条件。电阻电流
。电感和电容电流的方均根值相等,恰能构成电感和电容谐振的条件。电阻电流 与电压
与电压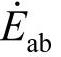 同相,电阻电流的方均根值是电感和电容电流方均根值的
同相,电阻电流的方均根值是电感和电容电流方均根值的 倍。由相量图可以得到此三相电流
倍。由相量图可以得到此三相电流 、
、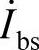 、
、 的方均根值相等,其相位差为120°。原来的单相电路经由上述平衡化电路,变换成了平衡的三相系统。从上述简单电路的平衡化方法可以推导出一般稳态系统的平衡化原理,即所谓Steinmetz原理,下面加以简单说明。
的方均根值相等,其相位差为120°。原来的单相电路经由上述平衡化电路,变换成了平衡的三相系统。从上述简单电路的平衡化方法可以推导出一般稳态系统的平衡化原理,即所谓Steinmetz原理,下面加以简单说明。
不平衡负荷如图3-60a所示,其中负荷导纳分别为Yab、Ybc、Yca,将其分解为实部与虚部,即电导与电纳
Yab=Gab+jBab
Ybc=Gbc+jBbc
Yca=Gca+jBca (3-70)
负荷补偿的基本思想是在原来负荷上并联三个纯无功负荷B∗ab、B∗bc、B∗ca,首先将负荷的无功部分抵消,使三相的功率因数均变为1。
B∗ab(1)=-Bab
B∗bc(1)=-Bbc
B∗ca(1)=-Bca (3-71)
此时整个负荷均为实数,即有功负荷,但是负荷仍然不平衡。为了平衡负荷,需要确定仍需补偿的分量。由于负荷为星形联结,所以零序分量为零,为了达到平衡,唯一所需的就是迫使负序分量为零。假定系统电压为对称的,即仅含正序分量,并且线电压的方均根值为1.0pu,电流的正序、负序和零序分量Ia1,Ia2,Ia0,可以利用式(3-72)得到。其中负序线电流为
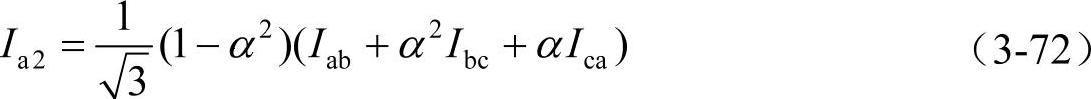
假定负荷的线电压分别为Uab=1、Ubc=α2、Uca=α,流经无功负荷的电流的负序分量,即负序电流的虚部可以表示为
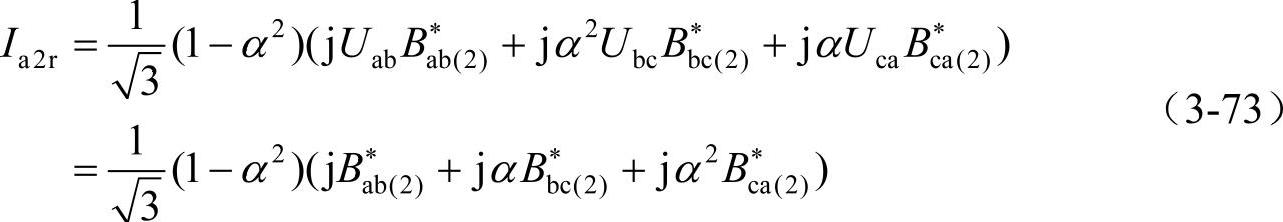
而流经纯阻性负荷的负序电流,即负序电流的实部可以表示为

为了达到负序电流为零的目的,应当满足
Ia2=Ia2r+Ia2a=0 (3-75)
由平衡补偿部分的正序分量得到其虚部,如下式所示:
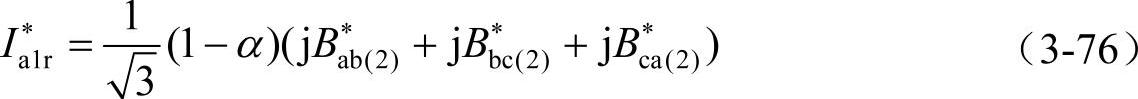
而由于补偿后功率因数为1,即I∗a1r应为零,即
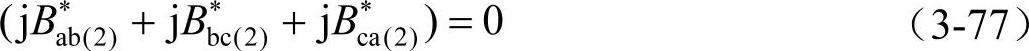
由式(3-73)、式(3-74)和式(3-77)可得到

上述方法将一个理想补偿网络与负荷相关联,就可以把任何一个不平衡的三相负荷变换成一个平衡的三相有功负荷,并且在变换同时还没有改变电源和负荷间的有功功率交换。式(3-78)同样可以利用负荷的有功和无功功率来表示,得到

比如,一个星形联结负荷的三相电纳以标幺值表示分别为
Yab=0.1333-j0.0667
Ybc=0.2667-j0.1333
Yca=0.1282-j0.0256
利用式(3-78)得到
B∗ab=-0.0133
B∗bc=0.1363
B∗ca=0.1025
假定负荷的线电压分别为Uab=1、Ubc=α2、Uca=α,得到线电流分别为
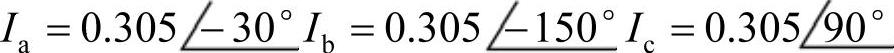
显然,尽管负荷中电流不同,但三个线电流是平衡的,也就是说从系统侧看,三相负荷是平衡的,相当于是三个阻值的标幺值为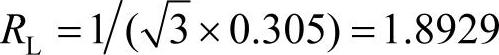 的星形联结的电阻负荷。一个值得注意的结果是
的星形联结的电阻负荷。一个值得注意的结果是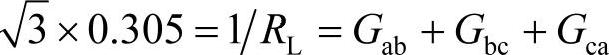 ,即补偿后每相的电导等于原电路三相电导之和。
,即补偿后每相的电导等于原电路三相电导之和。
上述讨论说明,可以利用Steinmetz方法将已知的不对称负荷通过在相间接入适当的无功负荷的方法来实现平衡。
Ghosh和Ledwich在文献[19]中提出一种利用使负序分量最小化的方法来直接控制母线电压。这种方法基于对无功分量的反馈控制而不是前述的阻抗测量,从而可将输电系统和其他不平衡电源的影响均考虑在内。
假定补偿器的电压与正序分量之间的夹角为θ,则线电流为

假定控制目标为使电流的无功分量正比于电压幅值与平衡电压的偏差,则

无功电流在线路电抗jX上引起的相电压变化为
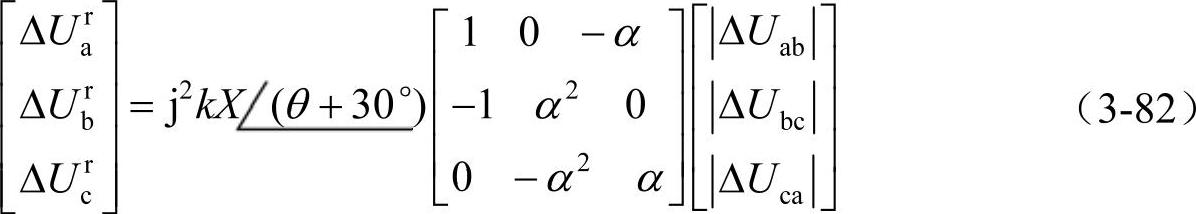
由此得到线电压的变化为

对于电压发生小扰动的场合,电压幅值的变化可以看作与相电压同相,可以近似得到
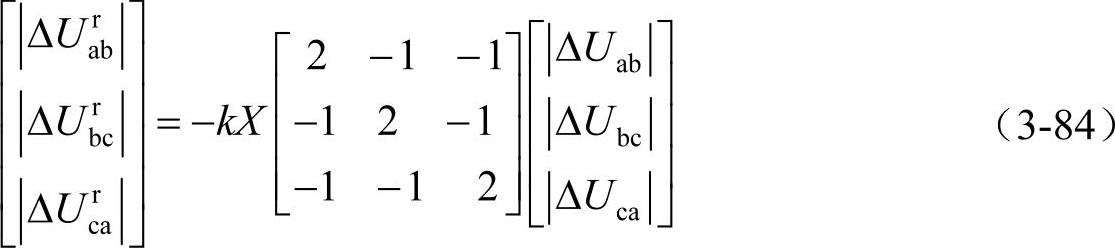
由于线电压中不含零序分量,所以式(3-84)可以进一步简化为

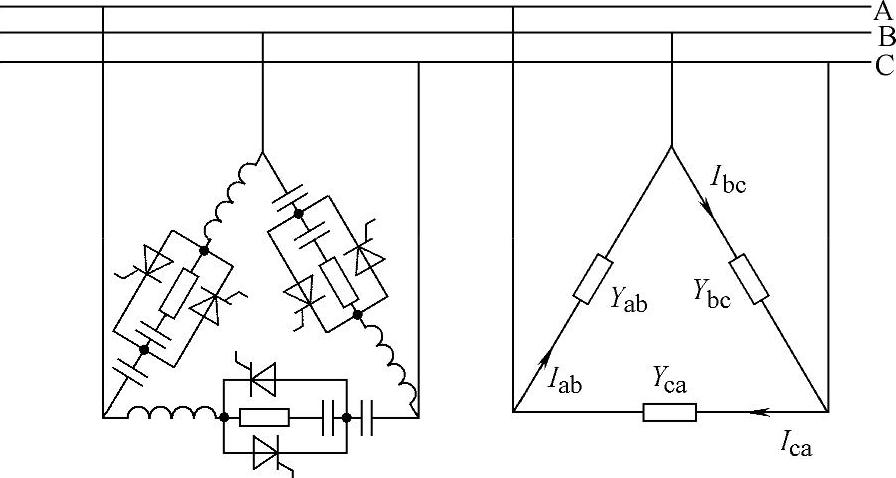
图3-61 利用TSC不平衡控制原理图
即补偿器对线路压降的校正是通过提供与线路电压变化幅值相等、相位相反的电压变化实现的。由于补偿器接为三角形,所以不能对零序误差进行补偿。因此,如果电压的不平衡度有限时,可以利用积分控制算法实现对电压不平衡和正序的补偿。图3-61所示为利用TSC对电压进行补偿的原理图,TSC电路中包括RC吸收回路、限流电抗和一对反并联的晶闸管。当AB线电压降低时,连接于相间的TSC按电压偏差控制,增加接入的电容量,以提高线间电压。TSC的三相独立控制可以达到平衡电压的目的,但仅适用于对电压跌落的补偿。
假定供电电压近似等于正序电压时,可以通过使流过补偿器的电流等于不平衡负荷产生的负序电流来实现补偿。仍然假定补偿器接成三角形,如果需要补偿器流过的负序电流为c+jd,正序电流为je,可以得到
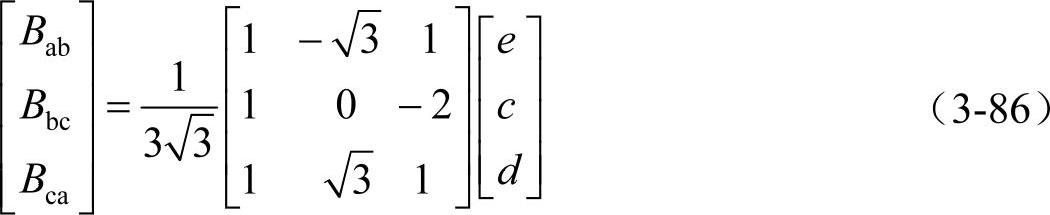
此算法通过所需的补偿电流来得到所需的导纳。通常,当不需零序补偿时,所有的电抗相等,但此方法仅适用于补偿器和负荷端电压为严格正序电压的场合。其他推荐的算法包括用瞬时电流采样法和利用有功或无功功率的平均值计算所需的补偿电纳,感兴趣的读者可以参考相应的文献。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




