振动沉拔桩机系统的数学模型与动力学特性分析

（1）振动沉拔桩机系统力学模型 振动沉拔桩机与土体相互作用，构成一个振动系统，由于土体的参振，该系统具有滞回特性。

若将土对桩的作用看做一个弹簧和一个阻尼器，那么振动沉拔桩系统的力学模型可视为在液压缸的作用下，机座和桩作两自由度的受迫振动。振动沉桩系统的力学模型如图12-13所示。图12-13a表示振动沉拔桩机的工作示意图，图12-13b为简化的振动沉拔桩机系统的力学模型。

图12-13 振动沉桩系统的力学模型

a）工作示意图 b）力学模型

（2）振动系统的运动方程 根据振动系统的力学模型和土的滞回模型，可以建立振动系统的动力学方程：

由式（12-36）和式（12-37）得

式中 m₁、m₂——夹紧器和机座的质量；

x₁、x₂——夹紧器和机座的位移；

k₂——隔振弹簧刚度；

F（t）——液压激振力；

f₀（x₁，x·₁）——沉桩阻力。

液压激振力F（t）由各次谐波力组成，可写为

式中 F₁、F₂、F₃——1、2、3次谐波激振力幅值；

ω——激振频率；

β、β₂、β₃——1、2、3次激振力的初相角；

t——时间。

显然，以上方程为非线性方程，可按非线性振动理论中的解析方法对其求解。

为加速对实际工况的逼近，可取非线性函数等于等效线性作用力加附加非线性作用力，即

式中 k_e——等效刚度；

c_e——等效阻力系数；

ε——小参数；——残余非线性函数。

所以模型的运动方程变为

（3）振动沉拔桩机系统的稳态响应

1）振动系统运动方程的非共振解。对以上方程进行一下变换：

代入方程（12-43）得

(www.xing528.com)

设方程的解为

x₁₀=acos（ω₀t+β）=acosψ （12-45）

f₀（a，ψ，θ）=f（acosψ，-aω₀sinψ，ωt） （12-48）而改进的一次近似解为

x₁₀=acosψ+εu₁（a，ψ，θ） （12-49）

由于阻尼的存在，自由振动将衰减为零，即x₁₀→0。实际上对工程有意义的是方程的强迫振动解，其振幅和相位差角为

等价线性化刚度和等效线性化阻尼可按下式计算：

2）弱非线性振动沉桩系统的共振。在共振情况下，外激励的圆频率ν和固有频率ω的差值为ε的同阶量，对于式（12-43），广义干扰力可以表示为

Q（θ，a，ψ）=εf（θ，ϕ₁acosψ，-ϕ₁aωsinψ）+εEsinθ （12-55）

其中，θ=ωt，ψ=θ+ϑ。

则方程式（12-43）的一次近似解可以表示为

x₁=ϕ₁acos（θ+ϑ）+εu₁+… （12-56）

其中，a和ϑ为

式中

Q₀（a，ψ）=εf（ϕ₁acosψ，-ϕ₁aω₀₁sinψ） （12-59）

令

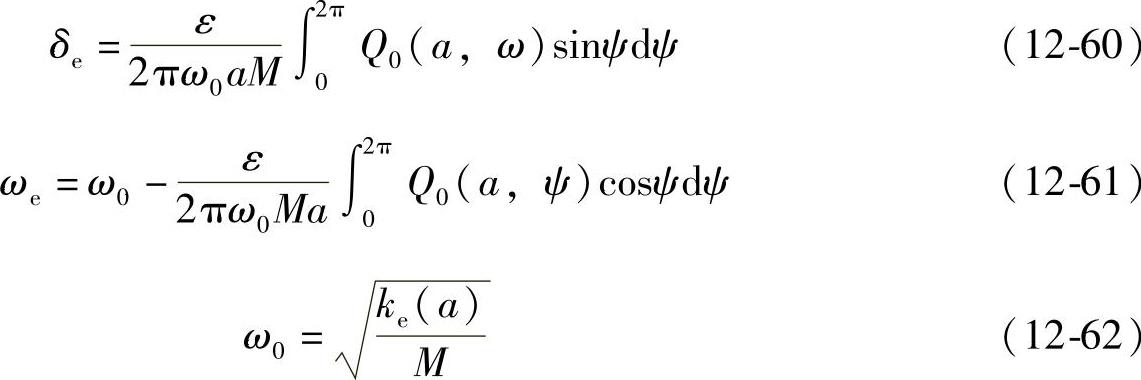
进行分段积分，即得

则振幅和相位在共振区域满足

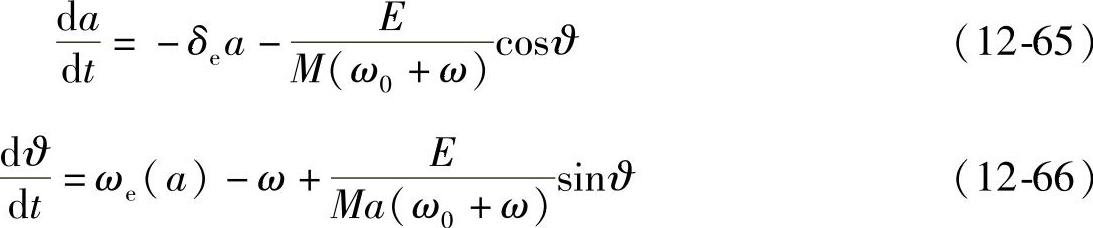
对于定常过程，振幅和相位不随时间变化，即

由此可得幅频、相频特征曲线方程

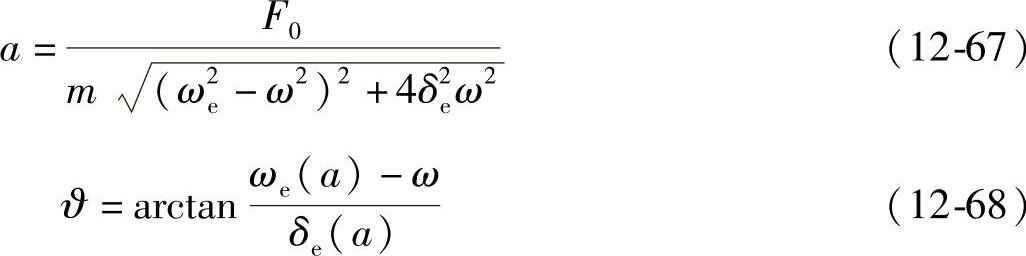
图12-14为振动沉拔桩机的双线性滞回模型稳态共振响应曲线。

图12-14 振动沉拔桩机双线性滞回模型稳态共振响应曲线

由图12-14可以看出，该振动沉拔桩机系统的幅频特征曲线具有软特性非线性系统的特点。