振动沉桩时土的力学模型优化

（1）滞回系统简介 滞回系统是包括非线性刚度及非线性阻尼的典型的非线性系统，在振动利用工程中具有广泛的实际背景。在工程中，滞回非线性一般来自工程材料特别是复合材料的非线性特性、接触面的摩擦特性以及结合面的接触变形等。在载荷作用下这些结构和系统的恢复力与位移之间存在着滞回关系，这种关系本质上是结构与系统变刚度能量损耗特征的描述。此外，这种关系还具有“记忆”特征，即系统的恢复力在任何瞬时不仅取决于在那个瞬时的激励和响应状态，而且也取决于其变形历程。当系统中有弹塑性构件或存在干摩擦时，在周期性荷载的作用下，作用力和系统位移或者应力和应变的关系曲线就可以形成滞回曲线。在工程中具有滞回恢复力的结构和元件很多。钢丝网类减振器是一种在工程上应用较广的新型非线性减振器，它是利用钢丝之间的干摩擦阻尼消耗振动系统的能量，从而达到减振的目的。这种类型减振器的恢复力和位移之间存在非线性滞回特性。粘弹性材料是近十几年来广泛用于减振降噪的一种新型材料，粘弹性材料在动态变形情况下，由于材料内部的能量损耗，使得其恢复力和位移之间呈现了非线性滞回特性，因此它也是一种同时呈现非线性刚度和阻尼的减振元件。在地震过程中，由于结构的塑性变形可以使结构消耗相当的输入能量，当结构进入弹塑性受力阶段时，其恢复力特性是呈非线性的，对于钢筋混凝土和钢结构等构件的恢复力—位移关系明显具有滞回性质。此外很多智能材料如压电陶瓷、形状记忆合金等输入电压与位移之间都表现出了滞回特性。滞回系统是包括了非线性刚度及非线性阻尼的典型非线性系统，在土木工程、机械工程以及控制工程等领域应用广泛。

对滞回非线性系统的研究已有三十多年的历史，目前已成为非线性动力学的主要研究方向之一。1960年Caughey应用Bogliubov和Mitropolsky的平均技术首先分析了双线性滞回非线性系统^[8]。这种双线性滞回系统是一种最简单的滞回系统，它仅能粗略地近似实际结构中的非线性现象，所以这种模型的分析结果与实际有较大的误差。由于缺乏合适的数学模型来模拟一般的滞回非线性系统，因而对于滞回非线性系统的研究进展非常缓慢。1967年，Bouc首先推荐了一个微分形式的数学模型来模拟滞回非线性系统^[9]，直到20世纪80年代前后，Wen与同事们才发展了这个数学模型^[10]，并使其系统化，从而使这个数学模型可以表示各种滞回线的滞回非线性系统。这个数学模型使人们可以较精确地研究滞回非线性系统的各种特性。但是，它是一个非解析的数学模型。

含滞回非线性恢复力的振动机械系统有振动成形机、振动压路机、振动沉拔桩机、利用振动使材料产生塑性变形的轧机等。振动压路机压实土壤的过程中，土壤随着带有振动的压实轮的运动，将产生弹性变形与塑性变形，当轮体向下运动时，压实作用力按弹性和塑性变形两个阶段变化。当轮体回程时，土壤已产生塑性变形，所以只能产生弹性变形。因此，振动压实的一个周期将出现不对称的滞回过程。

对于滞回曲线的区分，一般可以分为两大类：第一类是正阻尼型，它消耗系统的能量而使得系统的振动衰减，例如在土木工程中结构混合控制防震系统在地震、风载等外界激励下呈现出的滞回特性；材料的结构阻尼；非线性减振器由于干摩擦造成的滞回；振动压实过程中由于物料弹塑性变形而引起的滞回等。第二类是负阻尼型，它补充系统的能量而使振动加强，例如继电器的死区特性。

研究滞回系统的振动问题，首先应当建立滞回系统的数学模型。

由上可见，具有滞回非线性的系统和构件很多，它们的特性也不尽相同。由于滞回非线性是一种多值性的非解析系统，因此建立一个具有一般性能的滞回非线性系统的数学模型是极其困难的。

关于滞回系统的研究总是沿着两条方向进行的，一是关于滞回模型的建立；二是对滞回响应的研究。研究者从中抽象出来的滞回模型不下数十种，大致可以分为两大类，一是分段直线形滞回模型；另一类是曲线形滞回模型，下面对这两种类型中常用的模型作简单介绍。

最早提出的滞回模型是Caughy于1960年提出的双线性模型，这个模型具有对称性，是一种最简单的数学模型。在这个模型中系统的力—位移曲线由几个不同的线段组成，它所描述的曲线如图12-10所示。

它的物理系统可以认为是两个线性弹簧及库仑阻尼组合而成，有些文献利用该模型研究了振动压实过程中的不对称滞回模型。

（2）土的滞回模型 土体动本构关系的研究体现在本构理论分析、计算模拟和实验研究三个方面，三者之间相辅相成，互补发展。土体动力特性的早期研究限于实验条件简陋、分析手段落后，所建立的本构模型非常简单粗糙。随着技术的发展和分析方法的改进，人们对于动荷载下土体动力特性的认识日益深刻，模拟的结果越来越接近实际状态。目前，建立的土体动力本构关系模型已多达数十种^[12-14]。

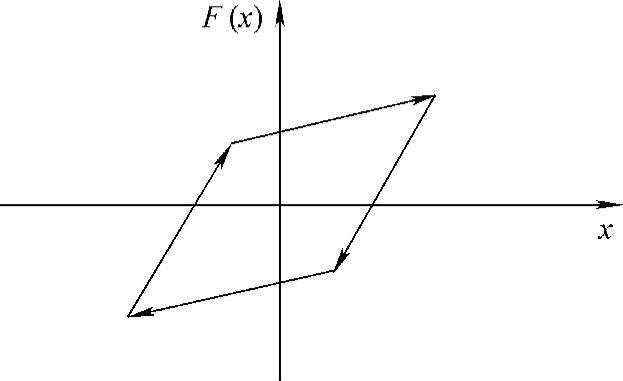
图12-10 Caughy双线性滞回模型曲线

土在周期荷载作用下的应力应变关系有两个特点，一个是非线性，另一个是滞后性。如果沿图中初始切应力为零的平面上缓慢循环加卸载，则在一个周期内的应力应变关系曲线将是一个滞回曲线（见图12-11）。滞回曲线反映出了应变的非线性及应变对应力的滞回性。

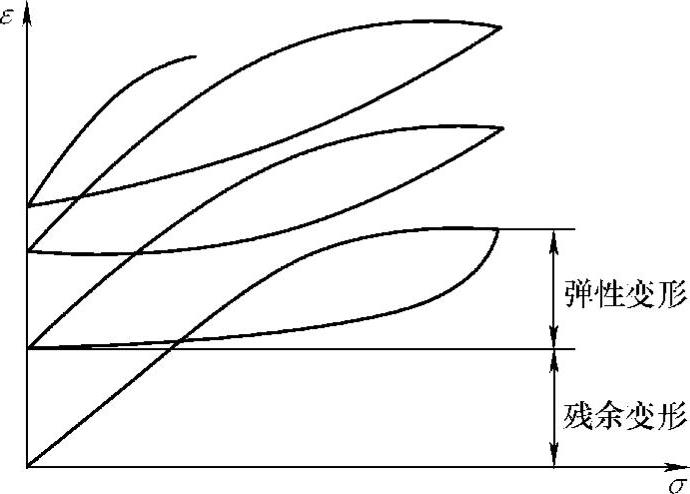
图12-11 土在压缩、回弹时的滞回曲线

土与一般的弹性材料不同，在受压缩时除部分弹性变形外还有相当部分是不可恢复的残余变形。土的弹性变形是指土在压力除去后可以恢复的那部分变形，例如土颗粒的弹性变形、封闭气体的压缩和溶解以及薄膜水的变形等。土的残余变形是指土在压力除去后不能恢复的那部分变形，例如由于土颗粒的相互位移、个别颗粒被压碎、孔隙水和空气从孔隙中挤出所形成的变形等。试验表明，振动沉桩时土的弹性变形比残余变形要小的多。(www.xing528.com)

随着激振力周期的增加。土的应力应变滞回环逐渐向应力增大的方向移动。对于软粘土，滞回环随向右移动而愈来愈大，愈来愈倾斜，出现周期衰化现象；对于松砂（干砂）滞回环随向右移动而愈来愈小，并愈来愈靠近，最终达到稳定状态。

振动沉桩时，桩尖将周期性的作用力加于桩端土，桩下沉时土产生弹性变形和塑性变形，而在回程中桩端土则以弹性变形为主。土在初始受到压力作用时，首先产生弹性变形，但变形量很小。由于在加载过程中土壤产生弹性变形和塑性变形且以塑性变形为主，而在卸载过程中主要产生弹性变形，从而造成了土壤滞回特性出现不对称特点。分析振动沉桩系统的力学特性，必须对土的不对称力学模型进行必要的简化。

把桩阻力f₀（t）看做由两个部分组成，一是桩测向滞回摩擦阻力；二是桩端阻力。桩侧滞回摩擦阻力可简化为双线性对称滞回模型。

滞回非线性作用力有多种形式，本章采用一种较为简单的平行四边形形式，如图12-12所示。

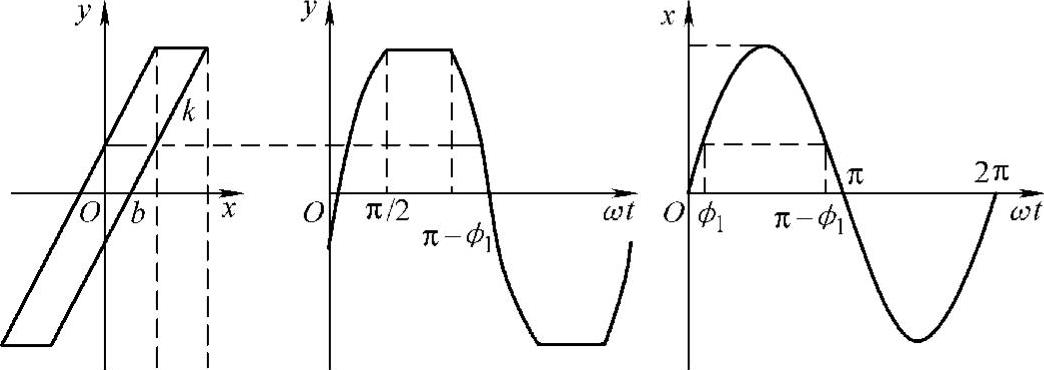
图12-12 平行四边形的滞回模型

沉桩阻力可近似按式（12-33）计算：

式中 f₀₁（x）——桩侧摩擦阻力；

f₀₂（x·）——桩端阻力。

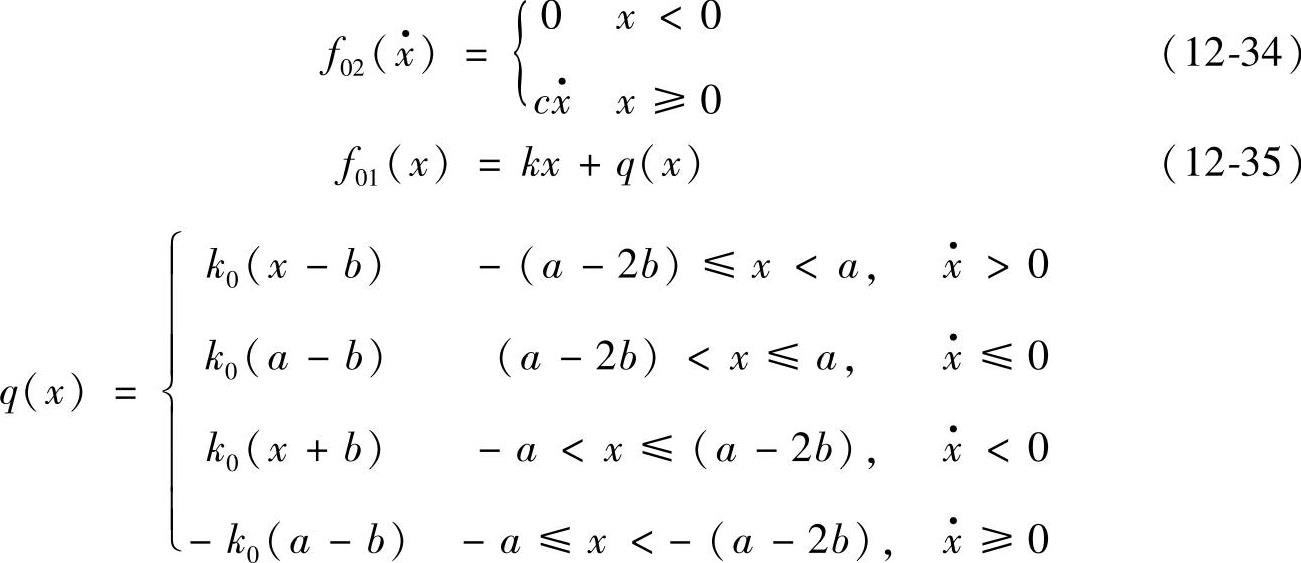
式中 a——次近似振幅；

b——滞回力折线转折点之坐标；

k₀——滞回线倾斜线之斜率；

c——阻力系数。