振动沉拔桩机动压油用回转换向阀的旋转阀结构

（1）旋转阀的结构 由于振动沉拔桩机动压油的振动频率较高，加之普通的换向阀结构和物理性能的限制，不能满足要求，因此采用回转换向阀。旋转阀是产生周期性脉冲激励的关键部件，其主要部件包括阀芯和阀套，结构如图12-6所示。其中阀芯的表面作镀铬处理。

阀芯体上有6个通孔，包括3个压力油孔，2个回油孔和1个卸压回油孔，通孔两端为矩形槽。阀套在通孔位置对应有6个圆孔，分别在阀芯一定位置时与阀芯通孔相通。

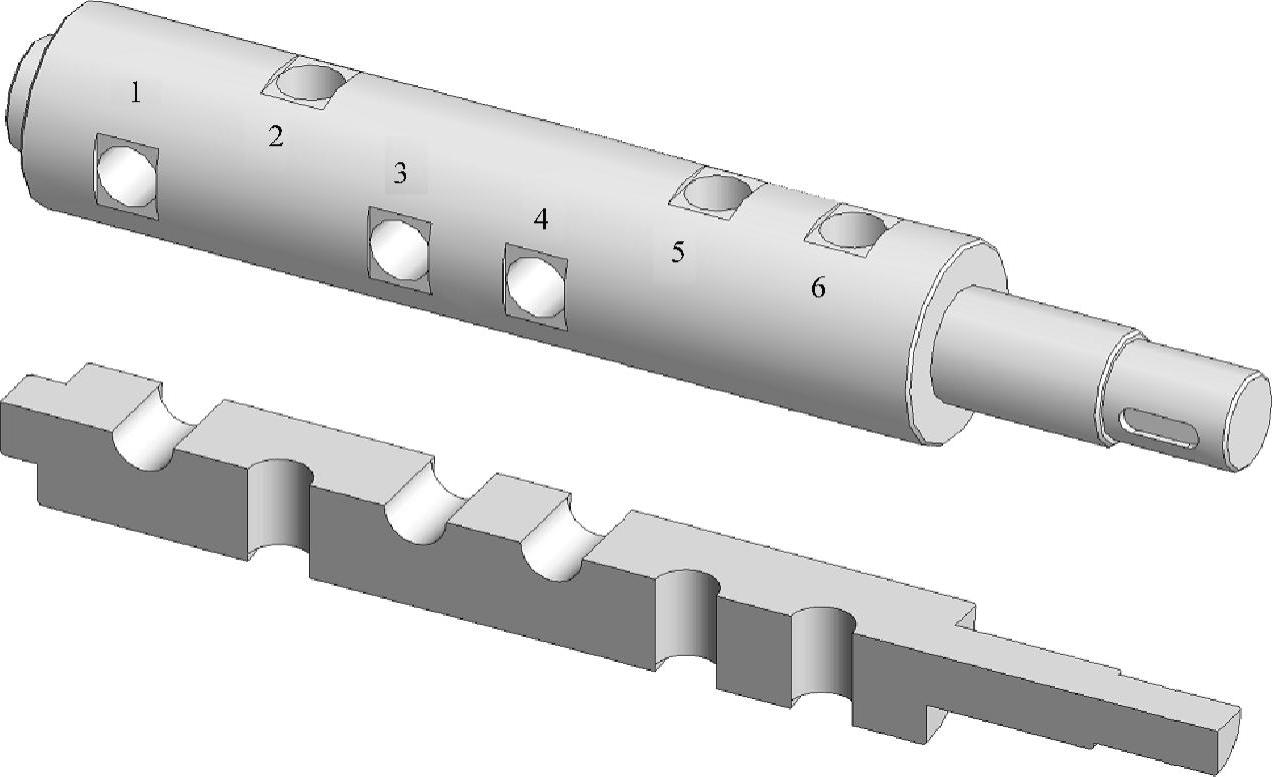
图12-6 旋转阀结构

注：图中序号为通孔号。

液压缸进、回油均通过旋转阀的油孔，高压、低压液压油交替进出。当旋转阀芯转到一定位置时，阀套上油孔通过油槽与高压油源相通，高压油进入液压缸前腔，转过一定角度后，油孔又与阀芯上回油油槽相通，高压油进入液压缸的后腔。

（2）过流面积 阀套上油孔与芯轴上矩形油槽重合的面积即为过流面积，如图12-7所示。

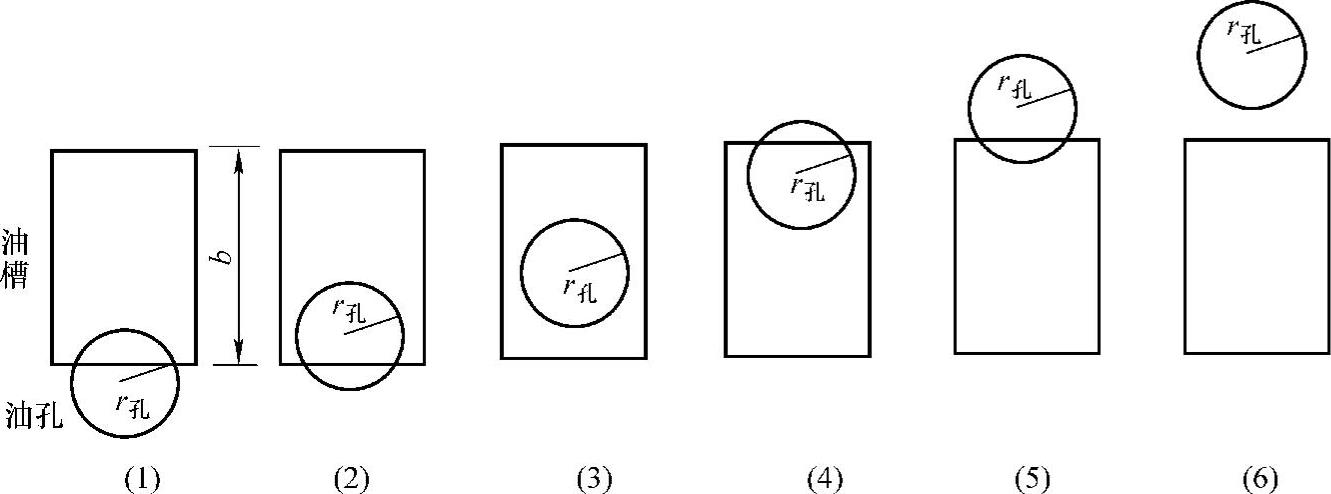
图12-7 过流面积

设芯轴以角速度2πv匀速转动，记θ=2πvt，θ₁为油槽边线偏离套上油孔边缘的角度，θ₁为

其中，INT为取整函数，过流面积A_过可以按油槽边线所处的位置的不同计算。

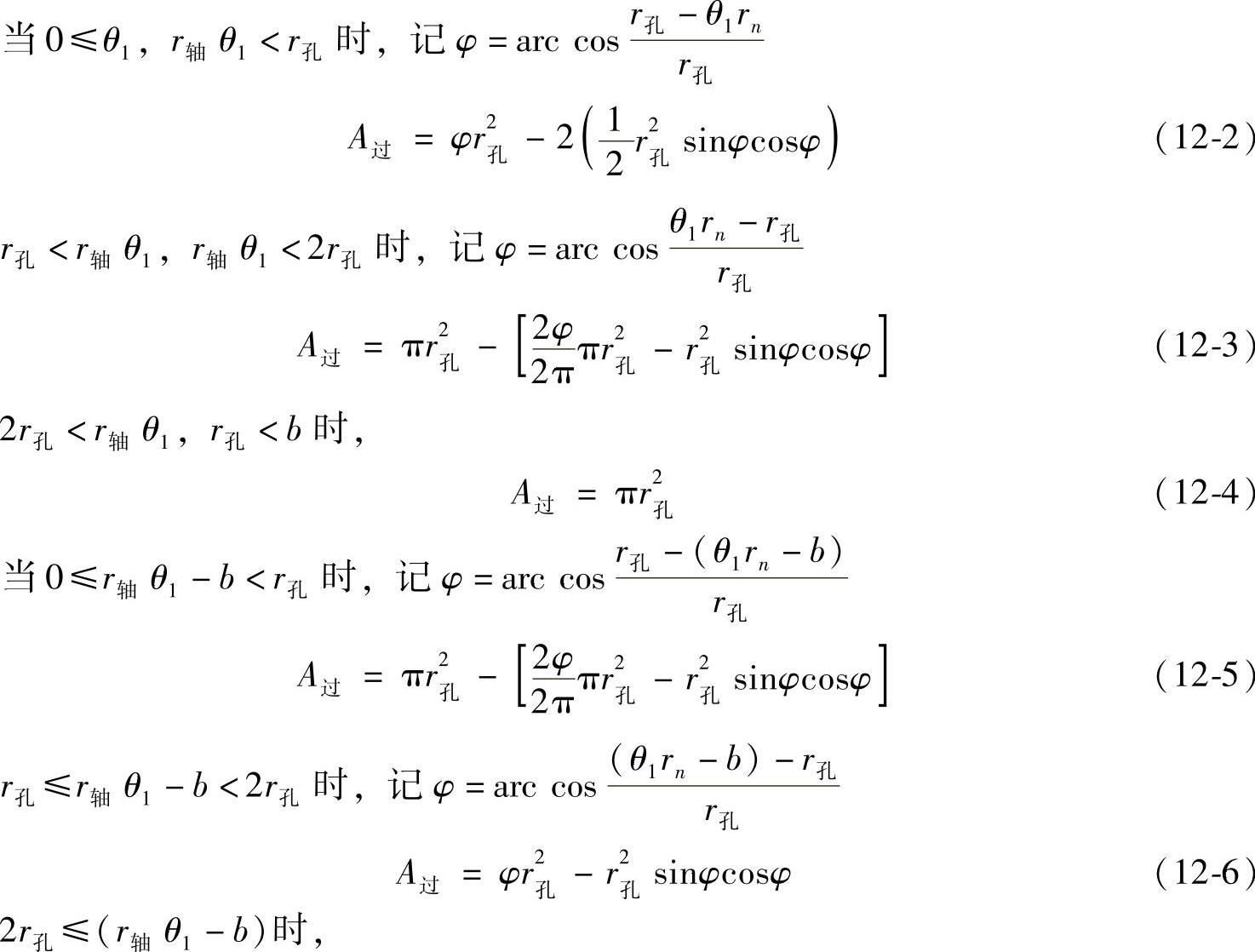
A_过=0 （12-7）

阀芯一个回转周期内，过流面积的变化如图12-8所示。

（3）旋转阀的流量方程 旋转阀芯的油槽与油孔视为可变节流口，故负载流量是过流面积的函数为

Q_L=f（A_过，Δp） （12-8）

Δp为节流口的压降。设负载压力为p_L，由理想零位阀可以导出流量方程：

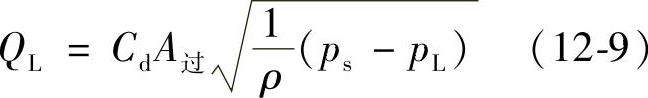
式中C_d——流量系数；

ρ——油液密度；

p_s——油源压力。

为简化分析，用Taylor级数对上式在零位置展开，并取线性化近似。定义流量增益K_q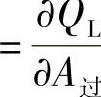，流量压力系数K_L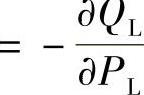和压力系数K_p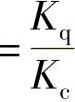，可导出线性化近似流量方程：

Q_L=K_qA_过-K_cP_L （12-10）

从以上公式可以看出旋转阀的流量和压力关系与普通滑阀具有相似的静特性。

（4）旋转阀控液压缸的连续性方程和力平衡方程 略去泄漏影响，液压缸的流量连续性方程为

其中，A_t为活塞杆受液压作用的有效面积。空载情况下，对于活塞杆，有如下力平衡方程：(www.xing528.com)

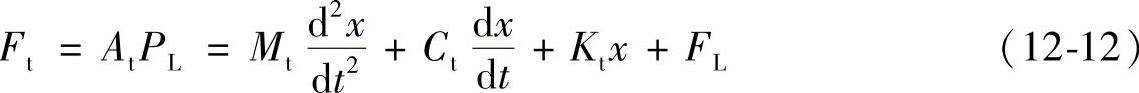
式中 M_t——活塞杆质量；

C_t——粘滞系数；

K_t——液压缸内液压油的弹性刚度；

F_L——活塞杆所受总反力，F_L=εQ_m，εQ_m为沉桩时土的作用力。

在这里可以视为小项，从而可以导出系统的运动方程为

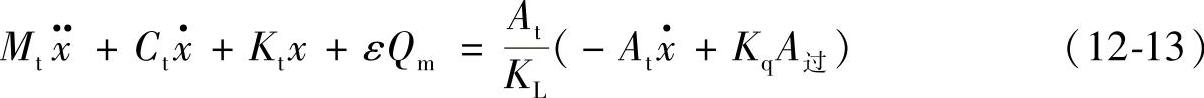
根据上述方程式可以求得其解。

上式可以写成：

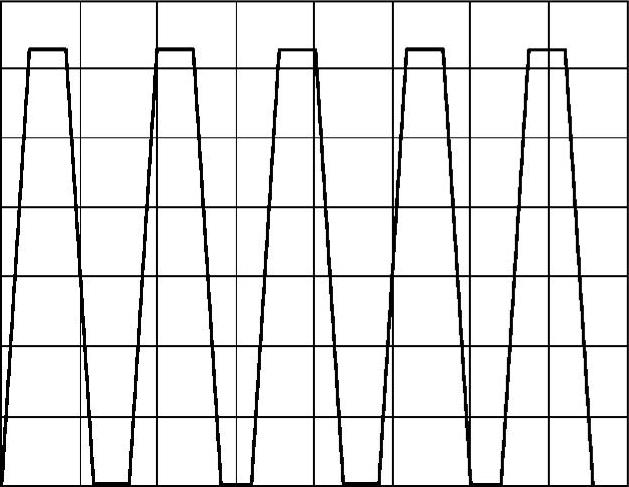
图12-8 一个回转周期内过流面积的变化

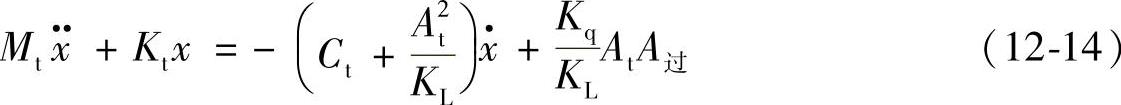
为简化分析，根据过流面积的特点，可设过流面积在0～φ₁～φ₂～φ₃～π各区段内按以下简单规律变化：

式中 φ₁，φ₂，φ₃——过流面积公式计算出；

C_A——过流面积变化速度系数。

设外力F为

由于A_过是周期函数，故F也是周期函数，用Fourier级数可将F展成谐波形式，然后继续进行分析。

将F用Fourier级数展开，前二阶谐波的系数为

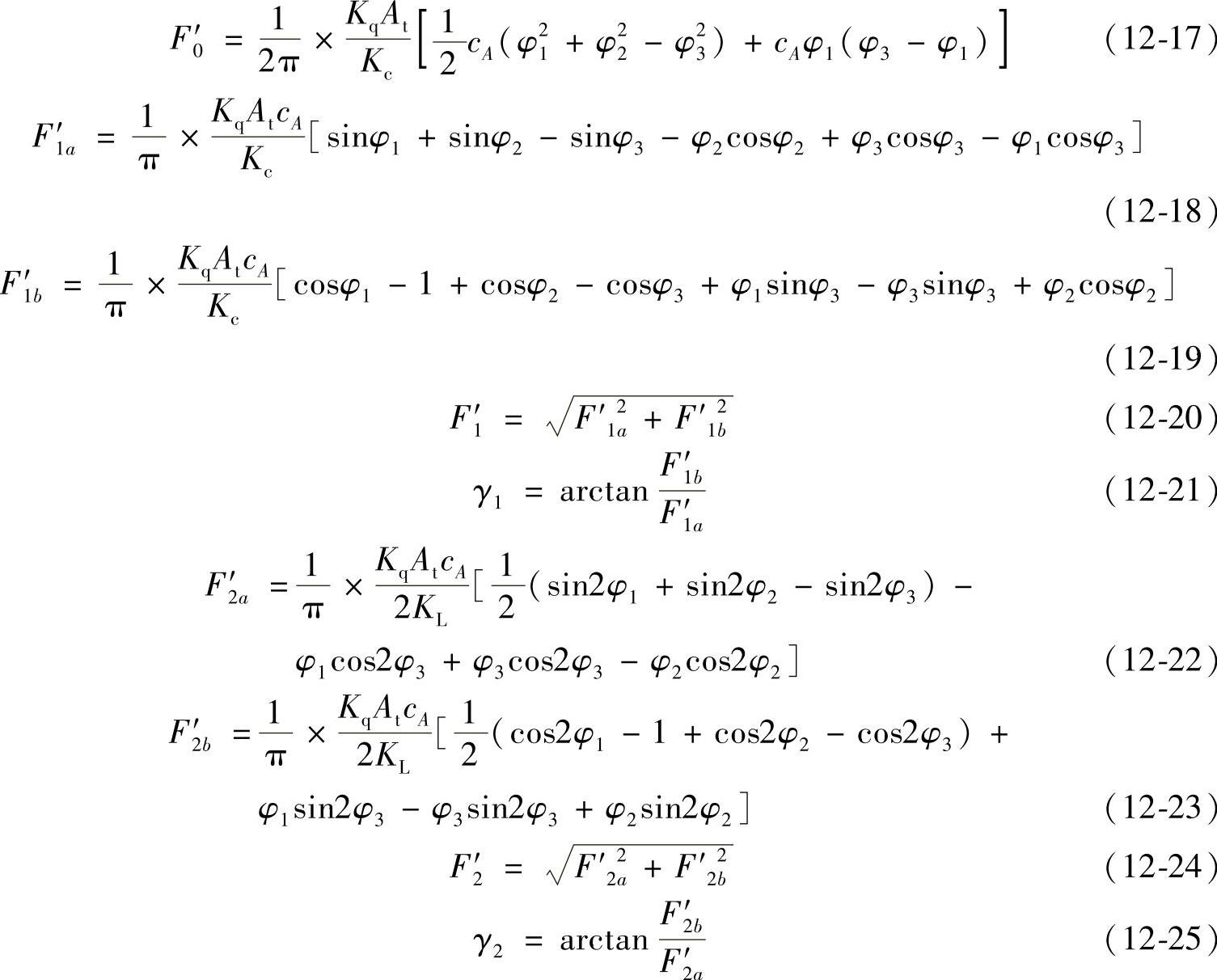
考虑到二次谐波，F近似为

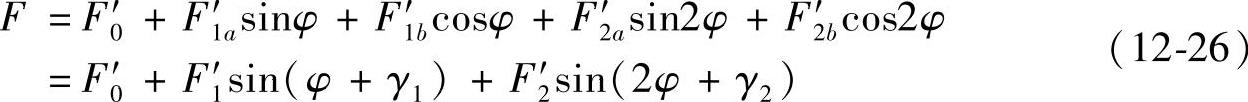
这样，原运动方程有如下形式的解：

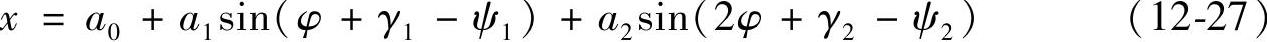
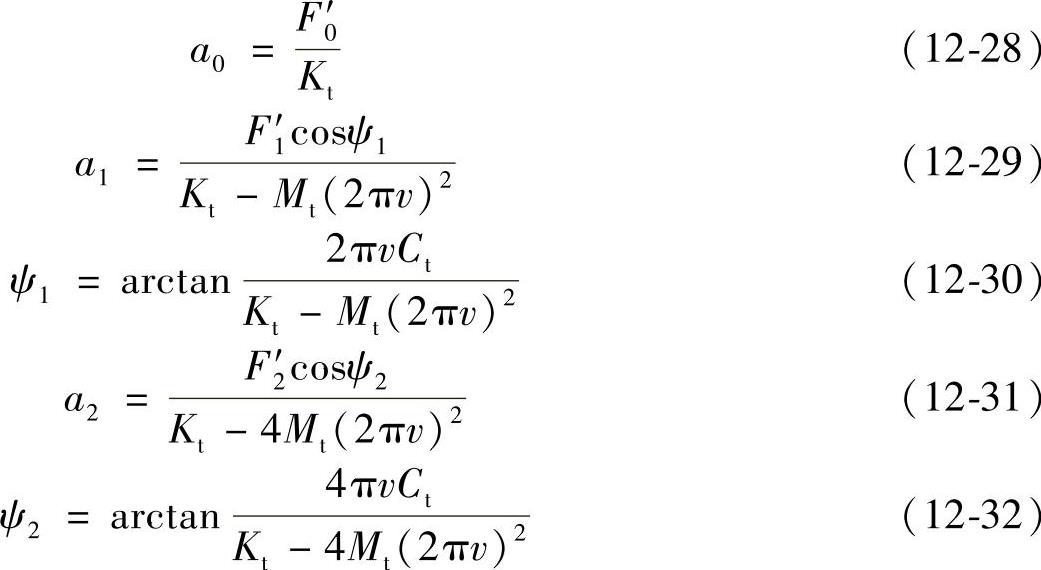
由液压脉冲激励的运动方程式可知，激振机构的运动为含有多个频率成分的周期运动。