多级模糊综合评价模型优化策略

所谓综合评判，就是要对某一对象进行全面的评价。对评价的对象往往要考虑很多因素。重要程度的不同，评级标准和自然状态的模糊等，也就是说，在作出任何一个决策时，都必须对多个相关因素作综合考虑，也就是综合评判。综合评判是系统工程的基本环节。其优点是：数学模型简单，容易掌握，对多因素、多层次的复杂问题评判效果比较好，是别的数学分支和模型难以代替的方法。在实际工程中，为了能够得到较为合理的评判结果，宜采用模糊综合评判法。

模糊综合评价的数学模型是由着眼因素集U，决策评价集V和模糊关系评价矩阵R构成的。

利用模糊综合评价方法对产品质量进行评价时，设着眼因素集合为

U_d={u_d，₁，u_d，₂，…，u_d，_m}，d=1，2，…，n （11-1）

定义因素集合U_d上的模糊子集为

A_d=（a_d，₁，a_d，₂，…，a_d，_m） （11-2）其中，a_d，_i为u_d，_i对A_d的隶属度，即因素u_d，_i在评定因素中起作用大小的度量，且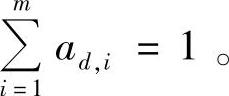

若评价域为

V_d={v_d，₁，v_d，₂，…，v_d，_n} （11-3）

则评价集合V_d上的等级模糊子集为

B_d=（b_d，₁，b_d，₂，…，b_d，_n） （11-4）其中，b_d，_j是等级v_d，_j对模糊子集B_d的隶属度。

于是，着眼因素集U_d到评价集V_d之间的模糊关系可以用模糊关系评价矩阵R_d来表示

其中，r_d，i_j=μ_R（u_d，_i，v_d，_j）表示单独考虑u_d，_i时，评价对象属于等级v_d，_j的隶属度，

且μ_Ai（a_d，_j）⇒[0，1]，μ_Bj（b_d，_j）⇒[0，1]，它们分别表示a_d，_i隶属于A_d和b_d，_j隶属于B_d的程度。

由此，综合评价的结果为

B_d=（b_d，1，bd，2，…，bd，n）=Ad。Rd （11-6）式中，“A_d。R_d”称为A_d与R_d的广义模糊运算，B_d为U_d的单一因素评价。而模糊合成运算模型主要有：M（∧，∨），M（●，∨），M（∧，），M（●，），M（●，+）。

模型1 M（∧，∨），有

式中，“∧”、“∨”分别为取小（min）和取大（max）运算，即

b_d，_j=max<min（a_d，₁，r_d，_1j），min（a_d，₂，r_d，_2j），…，min（a_d，_m，r_d，_mj）> （11-8）

此模型的意义是在决定b_d，_j时，对每个等级v_d，_j而言，只考虑调整后的隶属度r_d，_ij最大的起主要影响作用的那个因素，而忽略了其他因素的影响。由此可见，模型M（∧，∨）是一种“主因素决定型”的综合评判。

模型2 M（●，∨），有

其中，“●”为普通实数乘法，即(www.xing528.com)

b_d，_j=max（a_d，₁r_d，_1j，a_d，₂r_d，_2j，…，a_d，_mr_d，_mj）（11-10）此模型与模型M（∧，∨）的意义很相近，其区别仅在于M（●，∨）以a_d，_ir_d，_ij代替了M（∧，∨）的a_d，_i∧r_d，_ij，也就是说，用对r_d，_ij乘以一个小于1的系数来代替给a_d，_i∧r_d，_ij^{规定一个上限}。这里a_d，_i与在模型M（∧，∨）中一样，也起着调整系数的作用，此模型中也是用∨运算，所以也是一种“主因素突出型”的综合评判。

模型3 M（∧，），有

这里，a=min（1，a+），O为对m个数在运算下求和，即

由上式可以看出，与模型M（∧，∨）中一样，在模型M（∧，）中也是对r_d，_ij的规定上限a_d，_i给以r_d，_ij的调整，即有a_d，_i∧r_d，_ij，其区别在于，该模型是对各r_d，_ij作有上界相加以求b_d，_j。因此，a_d，_i也是在考虑多因素时r_d，_ij的调整系数，形式上这个模型是一种对每一等级v_d，_j都同时考虑各种因素的综合评判。

模型4 M（●，），有

即

此模型是在模型M（●，∨）的基础上改进而成的。模型M（●，）在决定b_d，j时，是用对调整后的a_d，_ir_d，_ij取上界和来代替模型M（●，∨）中对a_d，_ir_d，_ij取最大。

该模型有下列重要特点：

1）在决定各因素的评价对等级v_d，_j的隶属度b_d，_j时，考虑了所有因素u_d，_i的影响，而不是像模型M（●，∨）那样只考虑对b_d，_j影响程度最大的那个因素。

2）由于同时考虑到所有因素的影响，所以各a_d，_i的大小具有刻画各因素u_d，_i重要性程度的权系数的意义，因此，a_d，_i应满足=1要求。

所以模型M（●，）是一种“加权平均型”的综合评判。应指出，由于，_ir_d，_ij≤1，运算“”实际上已蜕化为普通实数加法“+”，因此，模型M（●，

)可改变成为模型M(●，+)。

模型5 M(．，+)，有

这里，“+”为普通实数的加法，权系数ad，i的和满足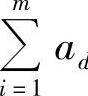，_i=1条件，模型中，式（11-6）右端蜕化为普通矩阵乘法。

由于机械产品总体质量包含的因素众多，为了避免信息丢失和综合考虑所有因素的影响，选用工程模糊综合评价数学模型中的“加权平均型”M（●，+）评价模型。

根据评价结果的b_d，_j中，数值最大者所对应的v_d，_j即可能为产品总体质量的一次评价等级，它是V_d上的一个模糊子集。由得到的一级评价结果B₁，B₂，…，B_n构成产品总体质量模糊评价的二级评价矩阵，即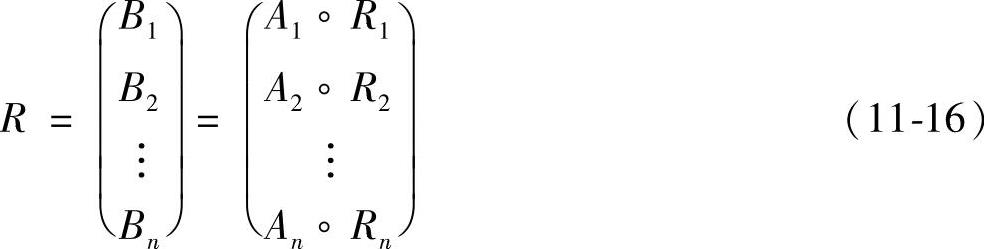

则得出产品总体质量综合评价的最后结果，即

B=A。R （11-17）

这也是着眼因素集U的综合评价结果，即

U={u₁，u₂，…，u_m} （11-18）