设计工作过程控制系统的最佳方案

在机器人进行与环境或操作对象接触的工作过程中，一般都存在从自由空间运动到受限运动的运动转换过程。当机器人以非零速度去接触受限环境时，由于动力学的不连续性，会导致较大的冲击，引起接触点处的振荡。在前面的仿真结果中可见，如果在运动转换过程中应用受限运动中的控制策略，冲击和振荡较大。因此，必须采用另外的控制策略使运动转换过程变得平滑与稳定，避免出现大的力冲击及振荡现象。在整个工作过程中的不同阶段，采用不同的控制策略和调用不同的64控制程序是控制的特点之一。下面就运动转换过程的控制问题做简要讨论。

转换过程中冲击力的大小取决于接触速度的大小、受限表面和机械手的刚度情况。设定机械手接触前后的动能分别为：k-=（1/2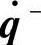）（）T M（q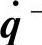）（）和k⁺=（1/2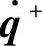）（）^TM（q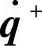）（），M为机械手的惯性量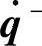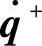，，分别为机械手接触受限表面前后的关节速度。撞击过程能量变化过程为

k^--k⁺=Δk （9-39）

在转换过程中的控制策略应设法吸收冲撞过程中的系统能量Δk。为了在转换过程中能尽快消耗机器人的初始接触能量，在机器人动力学模型中加入力冲击抑制项。转换过程的控制律采用Paqilla提出的非连续转换控制策略，控制律为

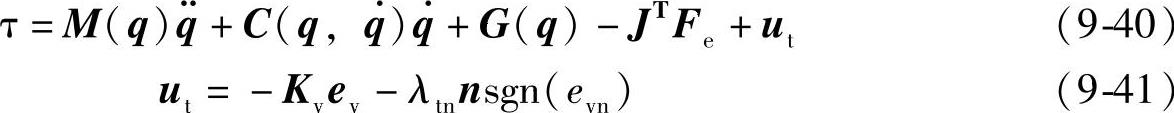
式中 K_v——正定的增益矩阵；

λ_tn——正的比例系数。

式中 n——法线向量：

λ_p——正定的增益矩阵：(www.xing528.com)

q_d——期望的关节速度；

e——关节位置误差。

在转换过程中采用式(9-40)所示的控制律，控制日标是使机械手末端满足一个匀减速的过程，当法向速度接近于零时，实际接触力也达到期望力的设定值。根据这个控制日标可以选定式(9-41)、式(9-42)中期望的关节变量、速度及比例参数。转换过程的结束标志是碰撞后的法向速度在规定的误差限之内。由于在转换过程和随后的受限运动过程采用不同的控制策略，为了使两种不同的控制策略平滑过渡，受限运动中第一个参考轨迹x_ro。采用转换过程后实际接触力第一次达到期望力时的末端实际轨迹。

本节联合非连续转换控制策略和基于位置反馈的预测算法进行了仿真研究，选择跟踪的受限表面仍是正弦曲线。初始速度为v_o。=0.7m/s，仿真初始点为(0.7，0.5)，在接触表面法线方向上期望力为30N，机械手末端沿椭圆表面的滑动摩擦因数为0.1。

在受限运动中，环境刚度的变化为

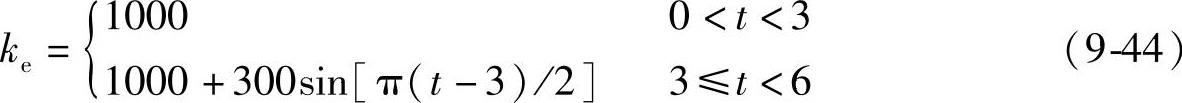
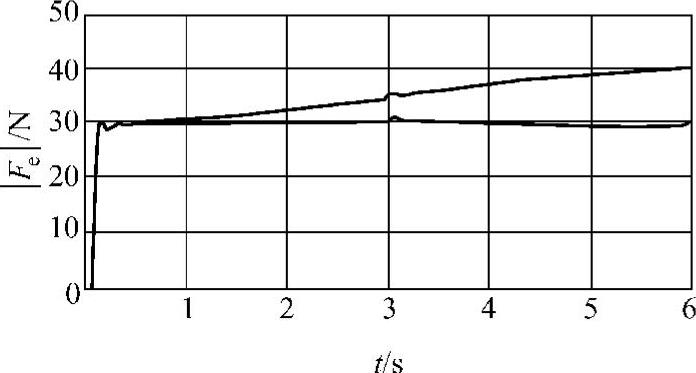
图9-31 应用非连续控制算法的力控制曲线

图9-31为在转换过程中应用非连续控制算法，在受限运动中应用位置反馈预测算法所得到的力控制曲线。由于在转换过程中加入了非连续控制算法，所以实际接触力在达到期望力后基本上没有大的冲击和振荡。