基于力反馈预测的阻抗模型仿真研究优化

为了验证力反馈预测算法的有效性，选择两自由度串联机械手沿正弦曲线表面进行力跟踪仿真。受限表面（正弦曲线）为

y=0.5+0.05sin[2（5x-4.5）]，x∈[0.7，1.1] （9-38）

力反馈预测算法跟踪的受限表面是正弦曲线中的凹凸部分，这样可以进一步验证算法对不同形状受限表面力跟踪的有效性，仿真示意如图9-27所示。机械手在自由空间某点以v₀=0.7m/s垂直向下去接触受限表面。仿真初始点为（0.7，0.46），在接触表面法线方向上期望力为10N，机械手末端沿椭圆表面的滑动摩擦因数为0.1。

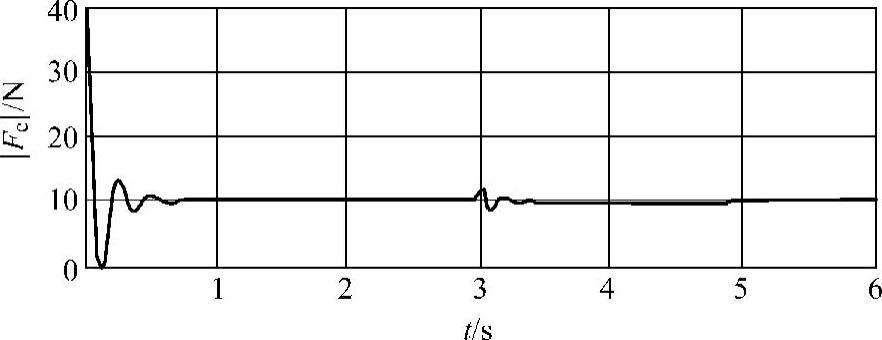
图9-28为应用力反馈预测算法所得到的力控制曲线。由于机械手以较大的初始速度垂直向下去接触受限表面，受到机械手惯性、重力的影响较大，因而在自由空间到约束空间的转换过程中有较大的冲击力，最大的冲击力达到34N。在随后的受限运动中，基于力反馈的预测算法根据力反馈信息对参考轨迹进行预测，可以有效地适应未知受限表面形状和刚度的变化，平稳过程中的力误差可以控制在±0.1N之间。

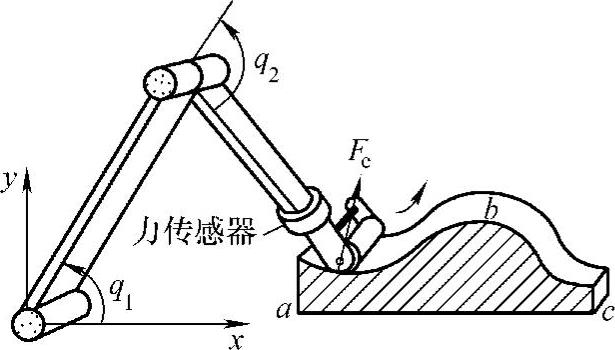
图9-27 机械手与受限环境的仿真示意图（正弦曲线）

图9-29为应用力反馈预测算法得到的机械手末端轨迹与参考轨迹的对比曲线。图中曲线1为受限表面未发生变形的轨迹（环境轨迹），曲线2为力反馈预测算法得到的参考轨迹，曲线3为机械手末端的实际轨迹。由图9-29中实际轨迹可见，在刚度连续变化时（t＞3s），力反馈预测算法可以有效地对参考轨迹进行预测和调整，参考轨迹的变化反映了环境形状和刚度变化的特点，得到的实际轨迹也能跟随参考轨迹的改变而变化，取得了较高的预测精度，受限运动平稳过程中的力误差仍可以控制在±0.1N之内。

(www.xing528.com)

图9-28 受限运动中的力控制曲线

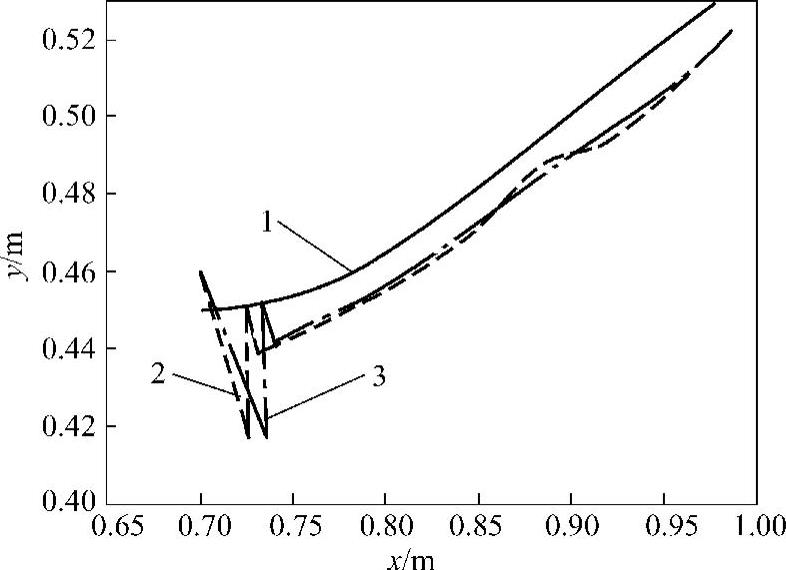
图9-29 机械手末端轨迹与参考轨迹的对比曲线

图9-30为力反馈预测算法得到的各个智能预测因子和预测方向角误差的变化曲线。对比图9-30a和图9-26a中满意度因子的调节曲线可以看出，在受限运动初期，由于受到较大冲击力的影响，在力反馈预测方式下满意度因子比位置反馈方式下（见图9-26a）有更大的调节幅度。在随后的受限运动中，它能够根据环境参数的变化进行调整，并保持在1左右（满意）。对比图9-30c和图9-26c中参考比例因子的调节曲线可以看出，两种反馈方式下的参考比例因子均根据接触力的变化而作出相应的调节，保证了预测精度。对比图9-30e和图9-26e中曲率适应因子的调节曲线可见，在两种反馈方式下选择跟踪的受限表面不同，因此曲率适应因子的调节过程略有不同。图9-30d为受限运动中预测方向角误差的变化曲线，在受限运动初期，力冲击对方向角的预测影响较大，因此预测误差较大。平稳过程中（t=1～6s），预测方向角的误差仍可以控制在[-0.005，+0.005]rad之内。图9-30b为阻抗参数的调节曲线，阻抗参数的在线调节提高了全局的力控制效果。

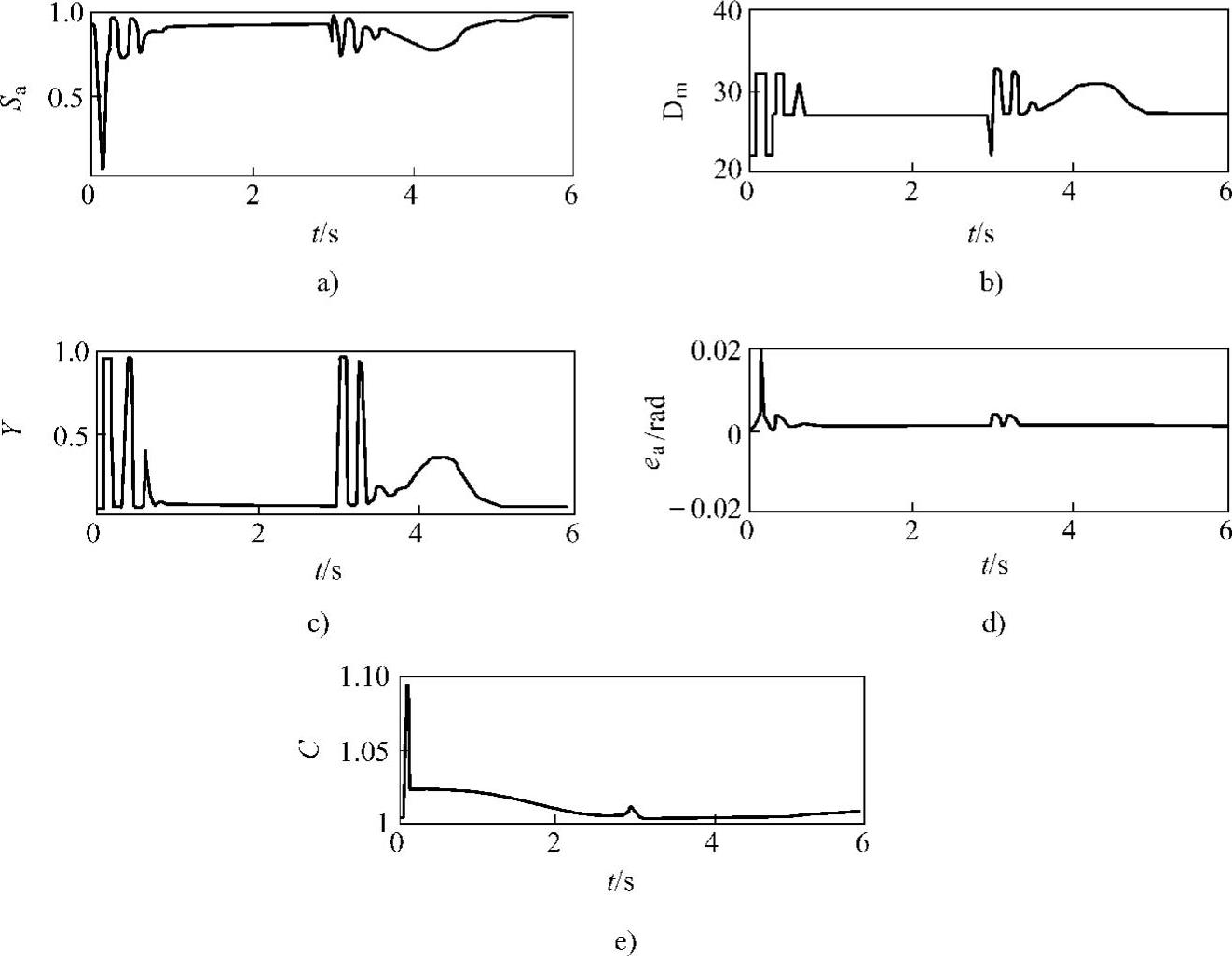
图9-30 智能预测因子和预测方向角误差的变化曲线（二）

a）满意度因子的调节曲线 b）阻抗参数的调节曲线 c）参考比例因子的调节曲线 d）预测方向角的误差变化曲线 e）曲率适应因子的调节曲线