智能预测参考轨迹

用传统的阻抗法进行力控制时，在确定阻抗模型中的参考轨迹时需要已知接触表面的几何信息。采用参考轨迹的模糊调节算法只能对未知接触环境的刚度变化进行补偿，当接触环境的几何形状信息也未知时，此算法不能使用。在实际中，接触环境的表面往往是非结构表面，这些表面的几何信息是不可预知的。因此，有必要在力控制中对这些未知环境的几何参数进行预测，使阻抗模型中参考轨迹对动态的接触过程具有适应性。

在受限运动中，机械手与受限表面的接触轨迹为一空间曲线。在特定的时间内，当机械手沿着受限表面某一固定的方向运动时，这条三维空间的接触轨迹变为二维空间内的平面轨迹。如果这条平面轨迹处处连续可导，则称为平滑轨迹，它所在的曲面称为平滑曲面。在大多数情况下，受限表面的变化较为平缓，例如：被擦拭的大型客机表面，被打磨的火箭发动机绝热层表面等。这里提出的智能预测算法主要是针对这类变化较为平缓的受限表面的。

针对形状变化较平缓的接触表面，利用前两个控制周期采样时刻的接触点位置，及前一控制周期接触力的变化情况，通过智能预测算法对阻抗模型中的参考轨迹x_r（k）进行预测，其离散形式为

值得注意的是，式（9-23）中的x（k-1）为前一采样时刻接触点位置，而并未采用上一控制周期的参考位置x_r（k-1），主要是避免预测误差的积累，保证预测的精度。v为接触点速度，t_m为采样周期，α_p（k）为预测方向角，预测参考轨迹如图9-20所示。预测方向角采用如下算法：

式中，α_p0为初始预测方向角的变化量；α_e（k-1）为通过反馈信息计算得到的真实方向角（见图9-20），真实方向角可以通过两种不同的方式得到。如果机器人系统中有高精度的位置伺服系统作为保障，并且系统传动环节的位置误差较小时，通过高精度的光电编码盘反馈得到关节位置信息后，真实方向角可以由已接触点的位置反馈值计算得到，设定（p_x，p_y）为笛卡尔坐标系下x方向和y方向的位置值，则α_e（k-1）可表示为

图9-20 预测参考轨迹

式中 α_e0——初始真实方向角的变化量。

另外，真实的方向角也可以通过力传感器的三维力信息（f_x，f_y，f_z）得到。设接触点环境的法向力为f_n，摩擦力为f_t。设摩擦因数为μ，两者的关系为

|f_t|=μ|f_n| （9-26）设接触点的合力为F（针对平面机器人，仅考虑二维空间），可以得到

F=f_n+f_t=f_x+f_y （9-27）它们的模满足

由式（9-28），推得(www.xing528.com)

由图9-20 所示方向角的关系可推得

由式（9-31）得

在实际的受限运动中，各个受限表面的摩擦因数不同，也较难确定，如果力跟踪速度较小时可忽略摩擦力的影响（f_t=0），以免引入不必要的误差。真实方向角可由式（9-32）变换得到：

α_e（k-1）=arctan[f_x（k-1）/f_y（k-1）] （9-33）

式中，f_x（k-1）、f_y（k-1）分别为当前采样时刻在笛卡儿坐标系中x、y方向的力分量，在实际系统中可由三维力传感器得到。定义n为当前时刻受限表面法线向量，n={cosα_n，sinα_n}，α_n为接触点的法线角，通过计算预测方向角的余角得到。

式（9-24）中s_a（k）为引入的满意度因子，s_a（k）∈[0，1]。满意度因子的引入是为了对以前的预测误差进行评估，借助前面的经验用于后面的控制，使系统具有学习的功能。δ（k）为每次预测方向角变化量，这里δ（k）=α_e（k-1）-α_e（k-2）。c（k）为引入的曲率适应因子，它的大小按预测方向角变化量的绝对值进行调节，曲率适应因子的引入是为了适应接触表面曲率的变化。

式（9-23）中，δx_r（k）=γ（k）φ_k，用来补偿包括环境刚度未知、力误差等因素所引起的预测误差。其中φ_k为参考轨迹增量的变化范围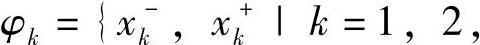，分别为每个采样周期内xr（k）调节的上下限，它的大小取决于受限运动中环境变形量的范围。m=t/t_m，t为受限运动的时间，这里引入参考比例因子y（k），y（k）∈[0，1]，它的大小可根据力误差在力控制环中调节。参考比例冈子的作用是间接调整参考轨迹的变化范围，适应环境刚度的变化，同时保证预测的精度。

方向角预测误差为

e_a（k）=d_e（k-l）一a_p（k-l） (9-34)