多机传动机械系统的运动控制优化

本节针对多机传动机械系统结构复杂，各电动机之间具有较强的动力学耦合性这一特点，以双电动机跟踪控制为例，提出一种基于模糊集合理论，通过在线识别电动机的机械特性，设计双电动机跟踪控制器控制方法。电网供电的电动机特性是转速与外负载的关系；变频器供电电动机特性是由变频器控制电压、外负载转矩与转速的关系。应用这种智能方法可实现在线自组织与自学习模糊控制器的设计。如通过电动机转速的变化预测电动机外负载的变化，进一步预测到各电动机之间的动力学耦合关系、能量的传递关系等，进而采取相应的控制策略，生成针对这一特性机械系统的模糊控制器。

（1）双电动机速度跟踪同步自组织模糊控制系统设计

1）系统的组成。自组织模糊控制系统的特点是能够自动获得系统的模糊控制器规则。模糊控制系统的关键问题就是模糊控制规则的获取。图9-10为双电动机跟踪自组织模糊控制系统的组成图。自组织模糊控制规则库分如下三个基本步骤：

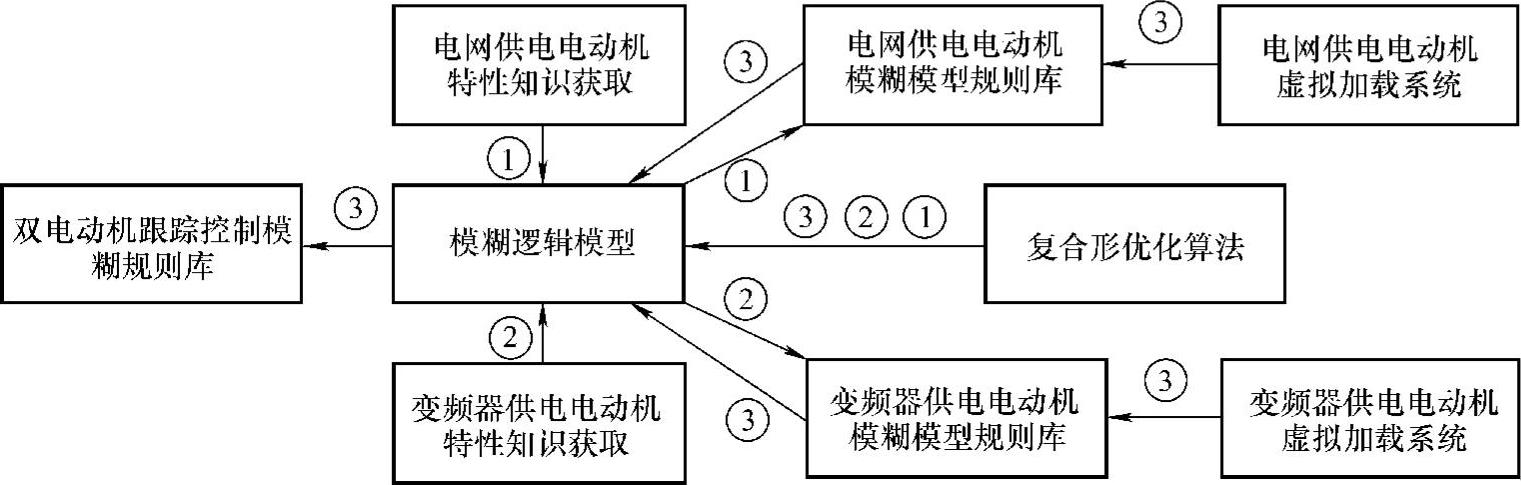
图9-10 双电动机跟踪自组织模糊控制系统的组成

① 电网供电电动机机械特性的获取。通过电动机加载和速度检测获得电网供电电动机的负载与转速的关系实测数据，利用复合形优化算法，对模糊逻辑模型进行优化处理，获取描述电网供电电动机机械特性描述的模糊规则。

② 变频器供电电动机机械特性的获取。通过改变变频器输入控制电压、电动机的外负载和检测速度，获得电动机转速与变频器控制电压及电机外负载的关系实测数据，再利用复合形优化算法，对模糊逻辑模型进行优化，进而得到描述变频器供电电动机机械特性的模糊规则。

③ 同步跟踪模糊控制规则的获取。通过对两个电动机模糊模型的虚拟加载，利用优化算法优化模糊控制逻辑，获得模糊控制规则，建立模糊规则库。

2）系统试验装置。为了用控制方法研究多机传动机械系统的同步控制，首先，需要掌握电动机在电源供电和变频器供电时的电磁转矩与转速的关系，即电动机机械特性。图9-11为在电源供电和变频器供电时电动机的自组织自学习模糊控制的试验系统框图。其中计算机部分由一台PC机和一块采样过程控制板组成。电动机转速由8098单片机测试，测试结果通过采样过程控制板上的Intel 8255A并行口传给PC机。本试验目的在于：建立电动机在电网供电时的转速和电磁转矩的关系，即电动机的机械特性的研究；建立变频器供电时电动机的转速和电磁转矩的关系，为实现下一节的速度跟踪控制打下基础。试验过程为：把直流电动机接成发电机工作，作为交流电动机的外负载，通过直流电动机串联不同阻值的电阻，研究交流电动机的速度变化情况。由8098单片机的HSI高速输入口通过光电编码盘检测电动机的转速，通过8255并行口传给IBM486。由电压传感器和电流传感器检测发电机的输出功率，将其转化为交流电动机的外负载。

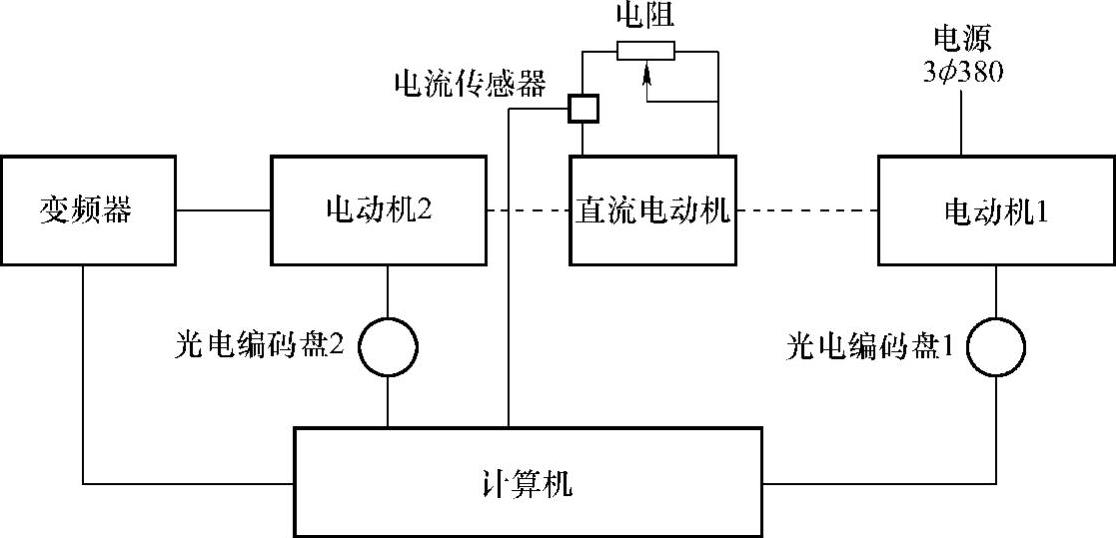
图9-11 自组织自学习模糊控制的试验系统

对于直流发电机，当励磁绕组的供电电压一定时，发电机的感应电动势与转子绕组的切割磁力线的速度直接相关。为此，本试验将直流发电机由交流电动机带动，交流电动机由变频器供电，而直流发电机的输出端串接一电阻。通过改变变频器的输入控制量，测得在不同转速下，发电机所串接电阻两端的电压值，即可求得发电机的感应电动势。若直流发电机的电枢回路内阻为R_s，外接电阻为R_w，测得外接电阻R_w两端的电压为U，电枢回路的电流为I_s，则根据电路克氏定律可得电势与电压的关系式为

E_s=U+I_sR_s （9-1）

发电机的输入功率P_I就是每秒钟内作用转矩对转子所做的功，其大小等于作用转矩与转子角速度的积，即P_I=Mω。而电磁转矩所做的机械功为M_dcω，它被转换为电枢电路中的电功率，此功称为电磁功率，用P_dc表示，于是有

P_dc=M_dcω （9-2）

从电路方面看，在电枢绕组和负载所构成的回路中，存在电枢电势E_s和电枢电流I_s，并且方向相同，则电枢电势E_s和电枢电流I_s的积就是电磁功率，即

那么，可以由式（9-2）、式（9-3）求得电磁转矩为

在直流发电机工作过程中，输入的机械功除了转换为电能外，还有铁耗、铜耗、机械损耗，附加损耗项，由于难于计算，这里将每一项给予4%的值，则输入转矩为

M_I=1.04M_dc （9-5）

（2）交流电动机在电源供电时的模糊模型实现速度跟踪的模糊控制，关键在于制定正确的模糊控制规则，所以必须掌握使用电动机的机械特性。在此，用直流电动机作交流电动机的外负载，通过将直流电动机的电枢绕组串接不同阻值的电阻，改变加在交流电动机上的外负载转矩。图9-12为电动机在电源供电时起动过程的转速、电压和电流的变化曲线。转速是由8098的HSI高速输入口测得的，8个脉冲宽度的电动机转速由起动—平稳运行—停机过程的速度变化规律。由图9-12可以观察到电动机在起动过程中，其转速超过了它的同步转速（1000r/min），图中的最大速度为1029.8r/min。许多计算机模拟的结果已经发现这一现象，这里的试验证明了这一点。由图9-12a的停机部分转速下降为直线可知，运行过程的机械阻力矩为常数，取其中的两个值：t₁=1.094543s时，n₁=960.00000r/min；t₂=3.910797s时，n₂=59.620820r/min。计算得其角加速度为ε=33.5542rad/s²，可以进一步计算得到传动系统的转动惯量J₀=0.0124kg·m²，系统的静摩擦转矩M₀=0.416N·m。将直流电动机的输出接不同的外负载电阻，可测得交流电动机稳态运行时的电磁转矩与转速的关系。交流电动机在稳态运行时电磁转矩与转速的关系为T_e=f（n），由电动机学可知这个函数是一个典型的非线性函数。由于模糊算子是一非线性万能逼近算子，所以在此通过试验测得实测数据，用模糊逻辑来逼近这一非线性关系。在试验中测得的实际转速转矩数据对（n_i，T_ei）作为输入输出的描述，为增加试验数据的可靠性，对于同一电阻检测K次，取其均值，作为系统特性的输入输出描述数据对。若一个工况试验M次，则

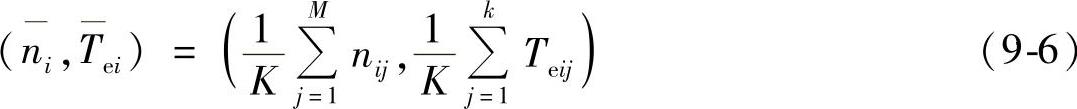
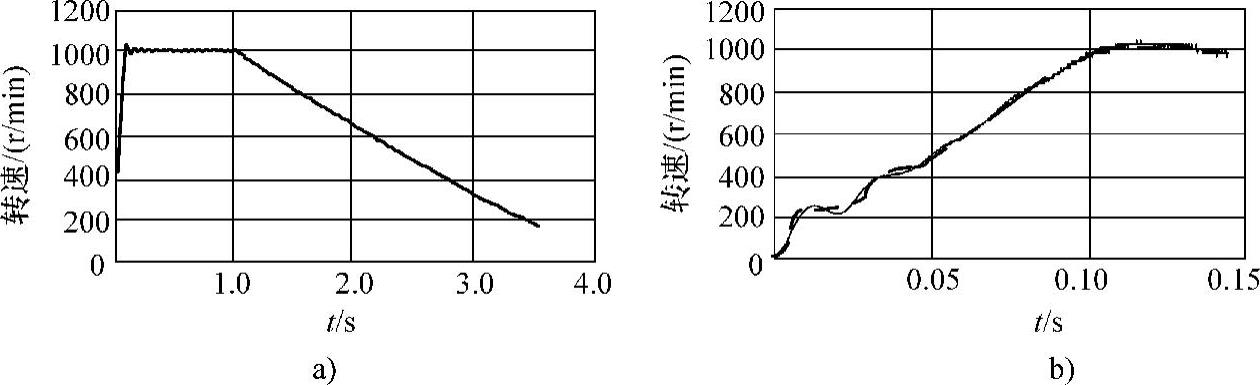
图9-12 电动机在电源起动过程的转速与电压及电流的关系曲线

a）转速与电压关系曲线 b）转速与电流关系曲线

这样，可获得描述电动机在电网供电下的转速—转矩描述数据对如下：

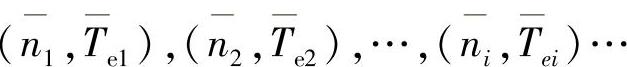
但交流电动机低速运行时，转速—转矩特性无法用上述方法获得，因为在低速时交流电动机工作时间超过一定的限度会被烧毁。所以将低速时电动机的转速—转矩特性用电动机起动过程的转速力矩关系近似代替，对图9-12的电动机起动过程采样，根据转矩、角加速度和转动惯量的关系获得转速—转矩数据对

（n₀₁，T₀₁），（n₀₂，T₀₂），…，（n_0i，T_0i）…

以模糊逻辑控制器映射电动机的转矩与转速的关系，模糊控制器的输入变量为电动机转速x，输出为电动机的电磁转矩，则对于稳态过程的模糊推理规则为

R_i∶if x isn_i，thenT_eisT_ei，i=1，2，…，N₀ （9-7）对于电动机的起动过程的模糊推理规则为

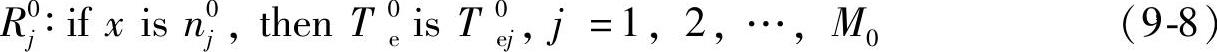
其中，n₁，n₂，…，n_N和n⁰₁，n⁰1，…，n⁰_M分别对应于电动机在电网供电时平稳运行和起动过程的模糊区间；N₀和M₀分别为稳态和起动过程的模糊模型中的规则数量。

选择三角形隶属度函数和面积重心非模糊化方法，则对于平稳工作过程的转矩转速关系为

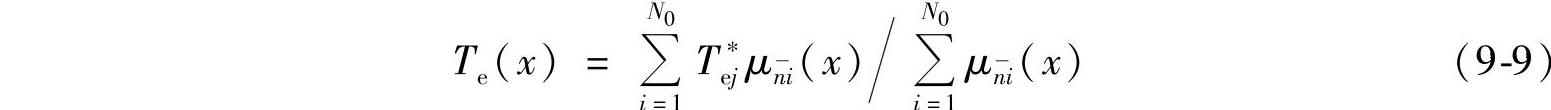
对于起动过程有

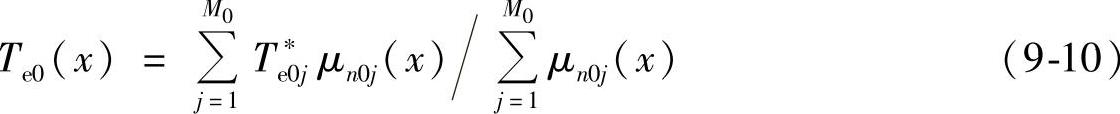
建立电网供电电动机模糊数学模型的关键是确定模糊区间n₁，n₂，…，n_N和n⁰₁，n⁰₁，…，n⁰_M以及对应支撑集的输出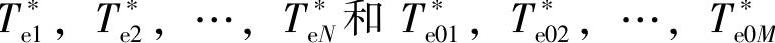利用复合形优化法进行优化，建立目标函数如下：

对于平稳过程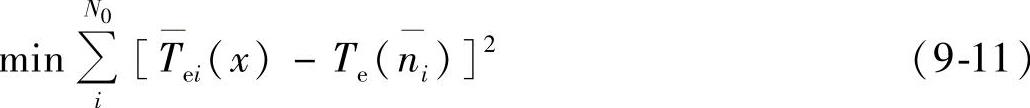

对于起动过程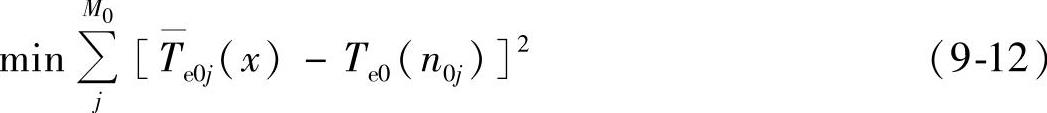

其中，N₀、M₀分别为平稳运行和启动过程采样数据的点数。从模糊逼近过程来看，模糊区间分得越细，则上述目标函数的值越小。而当区间分点与采样点相同时，误差为0。为了加快系统运行速度，逼近过程只要满足一定的精度即可。在此，将上述两目标函数的精度ε设定为0.01，对其进行优化计算。对式（9-11）通过采样获得30个点的稳态转矩值，根据交流电动机的机械特性推算获得10个点，共40个样本，对式（9-12）通过采样获取图9-12b的314个样本点，优化结果获40条规则，如图9-12b中的虚线。图9-13为交流电动机在电网供时的实测与模糊估计结果，优化结果获6条模糊规则，如表9-2所示。

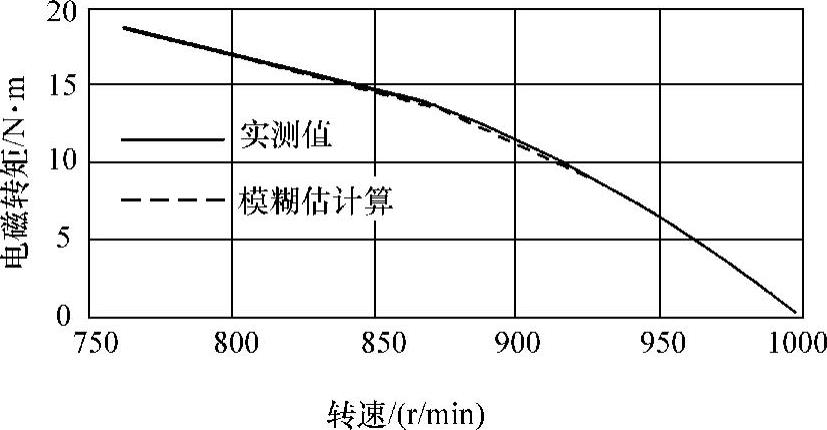
图9-13 交流电动机在电网供电时的实测与模糊估计结果

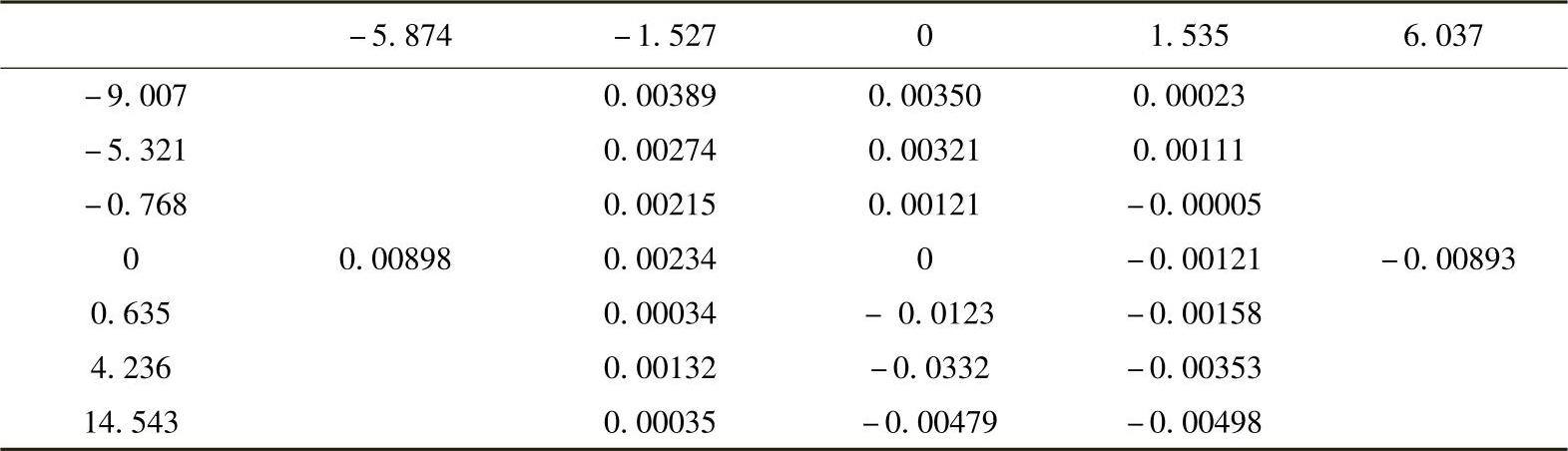
表9-2 交流电动机电磁转矩的模糊估计参数

∗表示推算段的结果。

（3）变频器供电时电动机的模糊模型 电动机2由变频器供电，将直流电动机接电阻作为交流电动机的外负载，变频器由计算机直接控制，其输入为0～5V的电压值。计算机控制变频器以不同的输入电压，检测出不同电动机转速的真实的

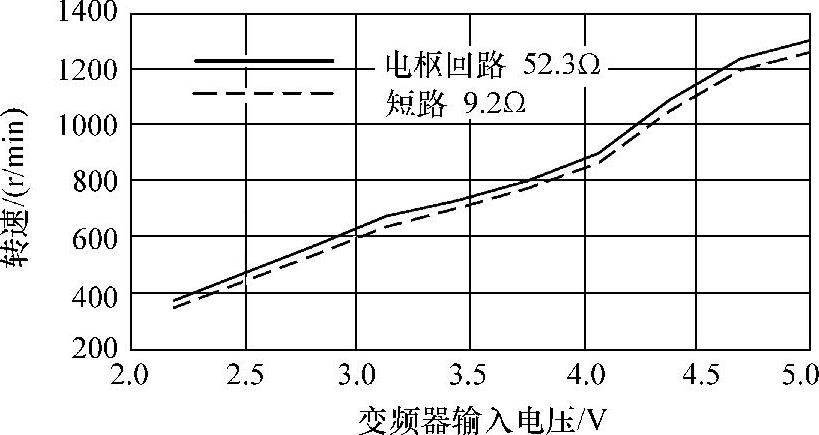
图9-14 直流电动机串接9.2Ω和52.3Ω电阻变频器以不同输入控制电压时的试验结果(www.xing528.com)

外负载值。图9-14为直流电动机串接9.2Ω和52.3Ω时，变频器输入从2.2V到5V时的试验结果。从图9-14可以看出，交流电动机的同步转速附近的机械特性曲线近似为一条直线，所以将交流电动机的变频供电时的同一输入控制电压下的机械特性近似地用直线表示。如控制电压输入为V_i时，在图9-13中对应两种外接电阻时测得的转速分别为n₁、n₂，电磁转矩分别为T_e1、T_e2，则机械特性近似直线段的斜率为

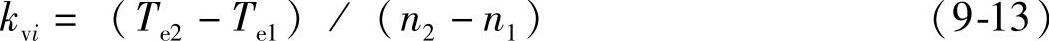
同步转速即为T_e=0时转速的值n_si，变频器在不同输入电压时的机械特性均以n_si、k_vi来描述。对于控制过程计算通过模糊插值获得。通过试验可测得如下描述变频器和电动机组合系统动力学特性的数据对

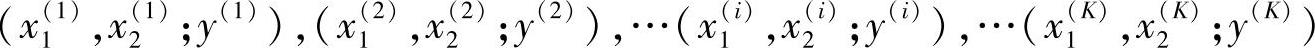
式中 x₁，x₂——变频器的输入电压和电动机的输出转速；

y——电动机的输出电磁转矩；

K——样本总数。

建立变频电动机数学模型描述的是当控制输入电压和转速一定时，估计输出电磁转矩。在同步控制过程中，将解决在当前外负载条件下电机转速如何变化，应采取什么样的调节措施。在此仍以模糊逻辑描述变频器电动机系统的力学特性。其模糊规则形式如下：

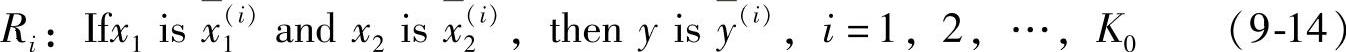
式中 [x₁^（i），x₂^（i），y^（i）]——模糊支撑集；

K₀——模糊规则数。

选取三角函数的隶属度函数，则对于变频器输入控制电压为x₁，电动机当前转速为x₂时，其电磁转矩为

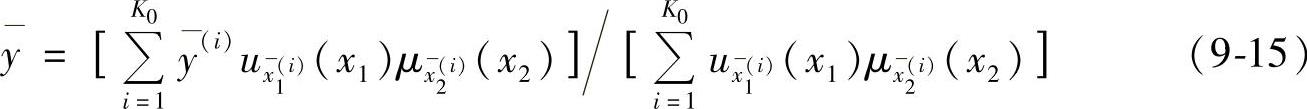
这时我们将以复合形优化法根据样本优化选取模糊集合。其目标函数为

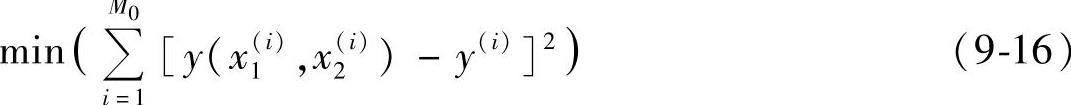
约束函数为

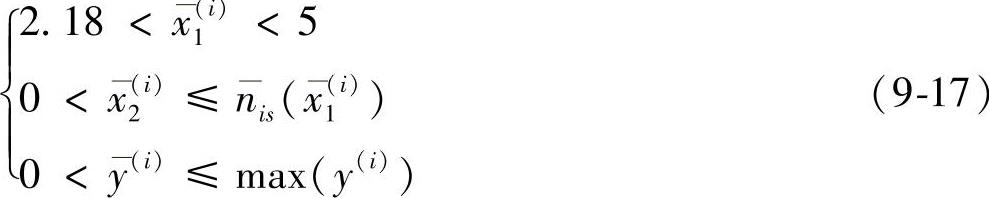
由于试验过程中，变频器的最低输入电压为9.18V，所以输入电压限制在试验范围内。将优化精度设为0.1，则优化获得168条模糊规则。

（4）双电动机跟踪模糊控制器的设计 式（9-9）和式（9-15）分别表示了电网供电和变频器供电时的电动机机械特性，根据这两式可以列出电动机1和电动机2转子的运动方程，即

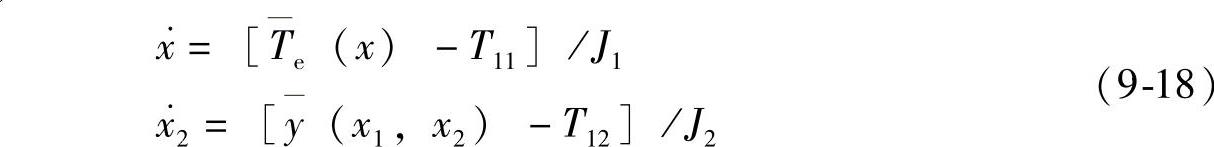
式中 J₁，J₂——电动机1和电动机2转子系统的转动惯量；

T_e（x）——电动机1的转矩，在起动过程中由式（9-10）计算，在平稳运行时，由式（9-11）计算；

T₁₁，T₁₂——电动机1和电动机2的外负载转矩。

设计电动机2跟踪电动机1的模糊控制器，以两个电动机的角速度差z₁=x₂-x和角加速度差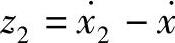为输入量，变频器的控制电动机调节量w=Δu为输出量。设z₁、z₂和w的作用域分别为[z₁^-，z₁⁺]，[z₂^-，z₂⁺]和[w^-，w⁺]。在控制过程中处于作用域以外的点用梯形规则来处理，在作用域内则采用三角形隶属函数。将z₁，z₂的域空间分别分成7份，标识为S3（Small 3），S2（Small 2），S1（Small1），CE（Center），B1（Big 1），B2（Big 2），B3（Big 3）。如前所述，对于每一区间给予相应的隶属度函数。则对双机同步跟踪控制器可建立如下的49条模糊控制规则：

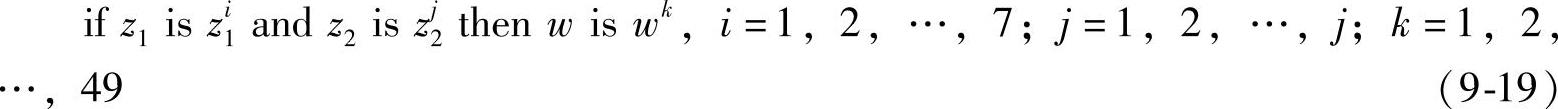
同步跟踪模糊控制器选择三角函数隶属度函数，模糊蕴涵选择乘积规则，模糊消除器选择中心平均形模糊消除器，即

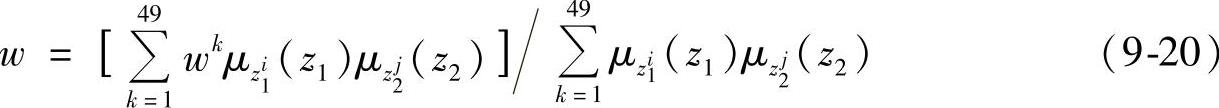
问题的关键是在当前电动机工作外负载的工况下确定z₁、z₂最优的模糊分区和相应的输出w，建立如下的目标函数：

根据系统运行的试验条件，建立如下的系统约束函数

使用复合形优化法对其进行优化。为了增加优化结果的可靠性，在优化过程中两个电动机分别施加不同的外负载，其模拟时间为t₀=6s，在0～0.5s，主电动机和从电动机同时受摩擦转矩T₁₁=T₁₂=M₀=0.416 N·m；在0.5～9.5s，主电动机外负载为T₁₁=9.5+4sin 2πt（N·m），从电动机所受外负载为平稳外负载T₁₂=4N·m；在9.5～4.5s，主电动机外负载T₁₁=12N·m，从电动机所受外负载为平稳外负载T₁₂=12+8sin 2πt（N·m）；在4.5～6s，主电动机外负载T₁₁=5N·m，从电动机所受外负载为平稳外负载T₁₂=10N·m。转速差和角加速度差的初始值分别在[-20r/min，20r/min]和[-20rad/s²，20rad/s²]，以0为中心两侧各随机地插入3个分点，即：x₁₁、x₁₂、x₁₃、x₁₄=0、x₁₅、x₁₆、x₁₇和x₂₁、x₂₂、x₂₃、x₂₄=0、x₂₅、x₂₆、x₂₇。模糊控制器的输出在[-0.1V，0.1V]内随机地选则点。优化结果如表9-3所示，表9-4为规则合并后的优化结果。图9-15为模糊控制优化的仿真结果。由表9-3第一轮的优化结果可见，在速度跟踪控制过程中，远离指令性速度时，控制指标的确定主要以速度差为主，仅当电动机转速趋近于指令性转速时才考虑角加速度的因素响应。这种结果也近似于人类控制的调节过程，反映出机器学习过程的复合形调优过程与人类经验的积累过程具有同样的特点。

表9-3 第一轮的优化结果

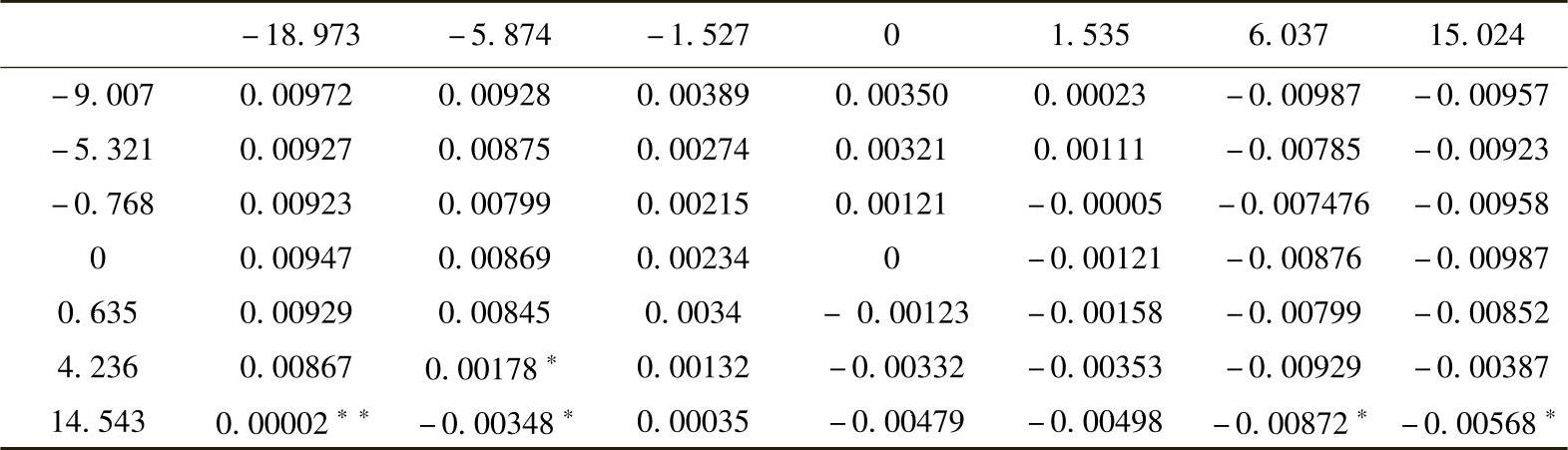
∗∗表示未使用过程的规则，∗表示使用少的规则。

表9-4 规则合并后的优化结果

（5）同步跟踪模糊控制试验 根据前面的优化结果，设计模糊控制器，对其优化结果的有效性进行验证。试验验证过程中分别对两个电动机空载运行、运行过程中对主电动机突然施加短路的直流电动机干扰、对从电动机突然施加短路的直流电动机干扰进行了同步控制试验，并作了主电动机突然施加短路的直流电动机干扰时的2∶1的恒速比跟踪试验。图9-16～图9-19为试验的结果。

将图9-15的计算机模拟结果和图9-16～图9-19的试验结果进行比较，图9-15的试验仿真结果主电动机超过同步转速24 r/min，从电动机转速起动阶段达1050r/min，有微量的超调。但实际试验的结果表明同步跟踪时从电动机超调达100r/min。仿真过程起动时从电动机可以较好地跟踪主电动机的转速，但试验结果表明从电动机的转速落后于主电动机。其原因在于系统建模是基于变频器供电时的稳态特性，而没有考虑变频器的响应滞后和瞬态特性所致，图9-16起动过程的转速比较可以看出主从电动机的转速比远大于2∶1，但当两个电动机的起动过程完成之后，稳态跟踪性能确实很好。从主从电动机受扰的情况看，当系统受外干扰以后，在极短的时间内稳定于同步转速。由此可见本节的优化模糊控制器具有较好的稳态跟踪性能。

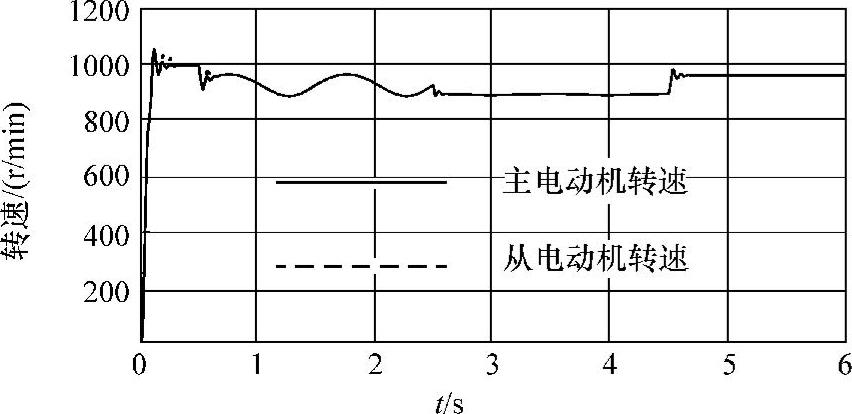
图9-15 模糊控制优化的仿真结果

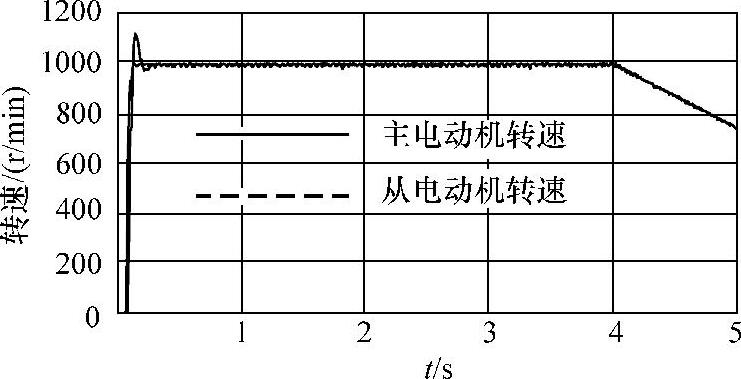
图9-16 双电动机空载速度跟踪同步控制的试验结果

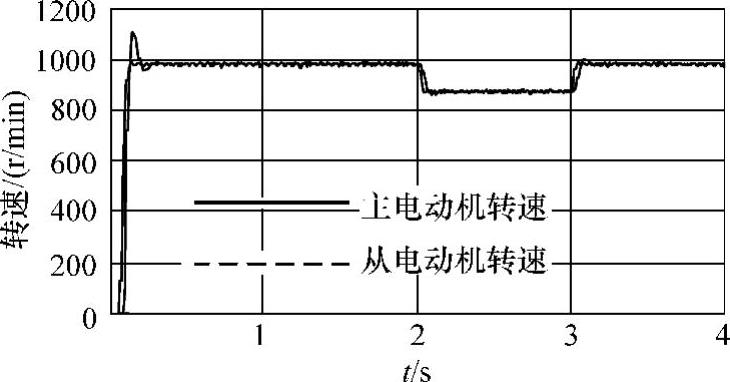
图9-17 主电动机2～3s受扰速度跟踪同步控制的试验结果

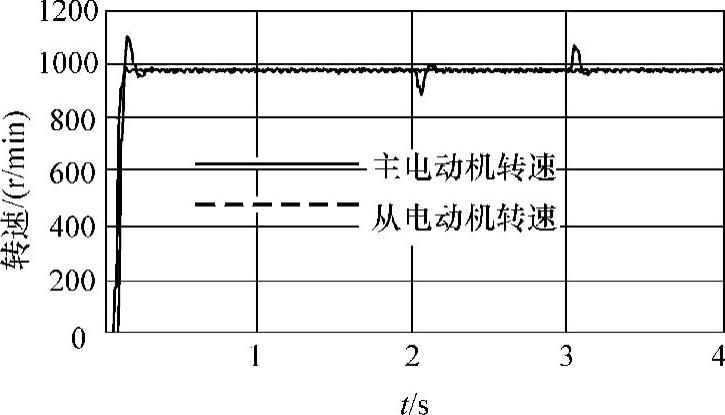
图9-18 从电动机2～3s受扰速度跟踪同步控制的试验结果

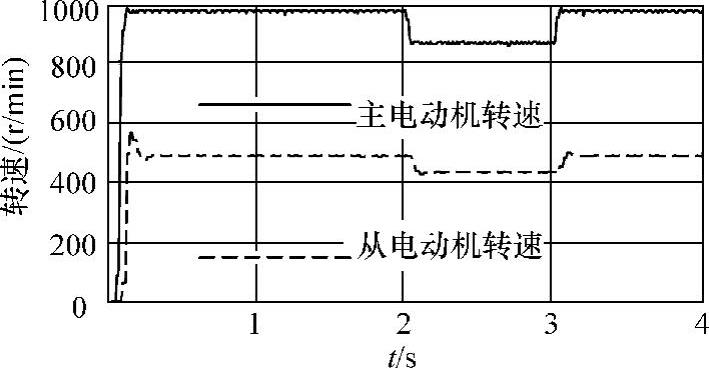
图9-19 主电动机2～3s受扰以2∶1速度跟踪同步控制的试验结果