如何计算弯曲振动系数

（1）弯曲振动对物料输送的影响 为了建立弯曲振动系数的概念，首先分析一下弯曲振动对物料输送的影响。

改变振动输送机实验样机的长度和工作频率，可以使之产生各种不同程度的弯曲振动。实验表明，在振动输送机发生弯曲振动的时候，槽体上每一点的振动都是刚体平移振动和弯曲振动的组合。在某些点上，这两种振动相位相同，而在另一些点上则相位相反。为了强调这种相位关系所产生的差别，特把弯曲振动曲线上刚体平移振动和弯曲振动相位相同的区域，定义为波峰，而把相位相反的区域定义为波谷。在波峰区域，刚体平移振动和弯曲振动的相位相同，因此合成振幅变大，

|S₂|＞|S₁|，振动方向角也变大，φ₂＞φ₁，如图8-25a所示。实验表明在波峰区域物料运动速度将加快。

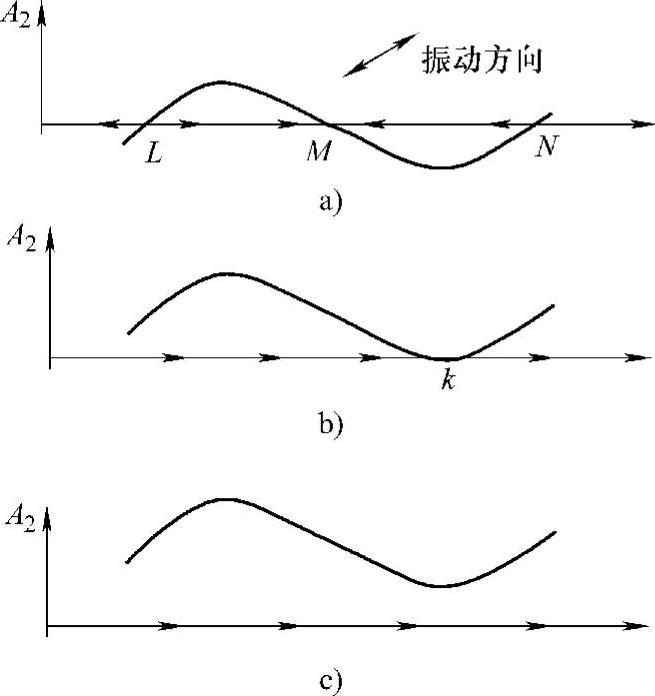
图8-24 振动方向角对物料输送的影响

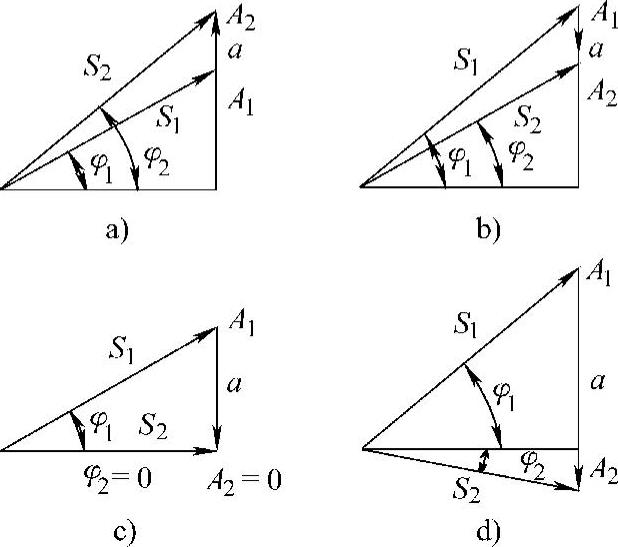
图8-25 各部位振幅和振动方向角的变化

S₁、φ₁、A₁分别为平移振动的振幅、振动方向角和平移振动的垂直分量，S₂、φ₂、A₂分别为合成振动的振幅、振动方向角和合成振幅的垂直分量，a为弯曲振动的振幅。

对于波谷区域可以分三种情况加以讨论：

1）在某点处|A₁|＞|a|。由于刚体平移振动和弯曲振动相位相反，合成振幅变小，|S₂|＜|S₁|，振动方向角变小，φ₂＜φ₁，如图8-25b所示。实验指出，在该点处，物料运动速度将减慢。

2）在某点处|A₁|=|a|。这种情况如图8-25c所示，此时振动方向角为零。实验指出，在该点处，物料不动或往复滑动，成为物料堆集点。

3）在某点处|A₁|＜|a|。此时振动方向角呈现负值，φ₂＜0，合成振幅的垂直分量与刚体平移振幅的垂直分量相位相反，如图8-25d所示，物料会出现反向滑动（也可能由于摩擦力很大而不动）。

这里所提出的结论，同德国的魏曼埃尔所得出的结论是不同的。魏曼埃尔认为，振动输送机在出现高频弯曲振动曲线时，有许许多多的拱段和节点。在振动曲线的拱段上输送速度有所提高，而在节点处则相反，将显著降低，所以在这些节点上，会发生物料堵塞现象。

（2）弯曲振动系数 严格说来，振动输送机的弯曲振动是普遍存在的，只是弯曲振动的程度不同而已。实际上，在槽体整个长度上出现微小的弯曲振动是无关紧要的，原因是它对槽体振动方向角及物料运动速度均没有明显的影响。但是当槽体出现较大的弯曲振动时，就会使其振动方向角发生明显变化，物料的运动速度在输送机的不同部位就会显著不同，从而使输送机的工作性能变坏，甚至不能正常工作。实践表明，振动输送机弯曲振动对工作性能的影响大小，同弯曲振幅与刚体平移振幅的比值有关。为了表征一台振动输送机弯曲振动的程度，本书在此引入弯曲振动系数的概念，并把它定义为

式中 a^∗——弯曲振动波峰或波谷处的最大振幅；

A——垂直于槽体方向的刚体平移振幅。

弯曲振动系数C同槽体各部位振动方向角及物料运动速度有着密切的关系：

1）当弯曲振动系数C＞1时，在波谷区域将有部分点的振动方向角变为负值，物料将出现反向滑动。对于二阶弯曲振型，在合成弯曲振动曲线上，将出现三个振动方向角为零的点L、M、N。如图8-24a所示。为清楚起见，把刚体平移振动与弯曲振动相位相同时的方向作为正方向（以后不再加以说明），图中箭头表示物料的运动趋势。在这种情况下，物料是不可能从槽体一端运动到另一端的。(www.xing528.com)

2）当弯曲振动系数C=1时，合成弯曲振动曲线上波谷区域的最低点k振动方向角变为零，物料将堆集在k点，如图8-24b所示。

3）当弯曲振动系数C＜1时，各部位振动方向角均为正，物料的运动趋势均朝着一个方向，如图8-24c所示。所以当弯曲振动系数C小于某一个接近1的数值时，物料将能够从槽体一端运动到另一端的。

使振动输送机试验样机产生各种不同程度的弯曲振动，观察物料的输送情况，观察结果与上面所作的分析完全一致。例如，长5.8m、频率2830次/min的自同步振动输送机试验样机，在激振电动机组位于一端2.15m及位于中间时，振幅曲线分别如图8-26所示，图中分别用箭头标出了实际观察的物料运动方向。在这两种情况下，弯曲振动系数大于1，所以物料都出现了反滑现象。

理论分析和试验均指出，弯曲振动系数C小于某一个接近于1的数时，物料即能够从槽体一端运动到另一端。但这绝不意味着振动输送机可以在这种状态下工作，因为在波峰处，振动方向角增大，合成振幅增大，物料以较快的速度向前运动；而在波谷处，振动方向角减小，合成振幅减小，物料以较慢的速度运动。这一方面会降低输送机的产量，另一方面仍有可能出现物料严重堆集以至堵料现象。因此弯曲振动系数C必须小于某一个特定数值时，物料才能实现正常输送。实践表明振动系数最好小于1/5～1/4，一般不应大于1/3～1/2。

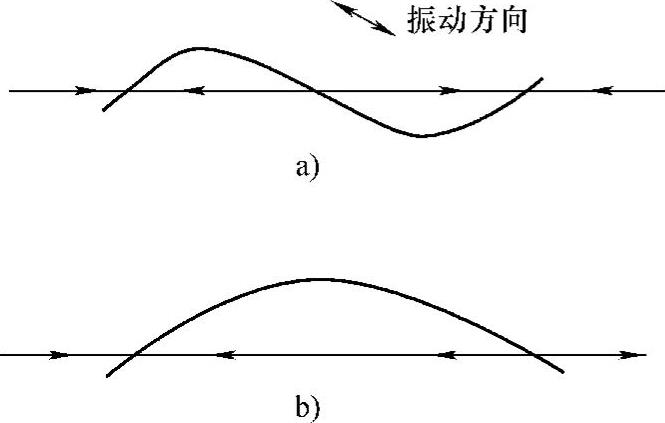
图8-26 实际观察的物料运动方向

总之，弯曲振动系数是一个表示弯曲振动程度的无因次量，也是衡量一台振动输送机工作性能好坏的重要标志之一。

（3）弯曲振动系数的计算 对于单质体振动输送机，可以采用前面所述的传递矩阵方法，求得槽体各部位的弯曲振幅a；对于双质体及多质体振动输送机，则可以用有限元法求得槽体各部位的弯曲振幅a，由计算结果容易找出弯曲振动的最大振幅a∗。而在设计振动输送机时，工作振幅是预先给定的参数。根据弯曲振动系数的定义，把a∗和A代入式（8-72），即可求出弯曲振动系数C。

（4）弯曲振动系数的实测 为了确定弯曲振动的许用值范围，先后对十几台振动输送机进行了实际观察与测量。实测结果表明，弯曲振动系数最好小于1/5～1/4，一般不应大于1/3～1/2，现举例说明如下：

某双管振动输送机用机械式万能测振仪，测得的数据列于表8-5和表8-6。根据上表可求得弯曲振动系数C（表中各参数的意义及数据整理方法可参阅文献[71]）：

表8-5 双管振动输送机1的实测参数

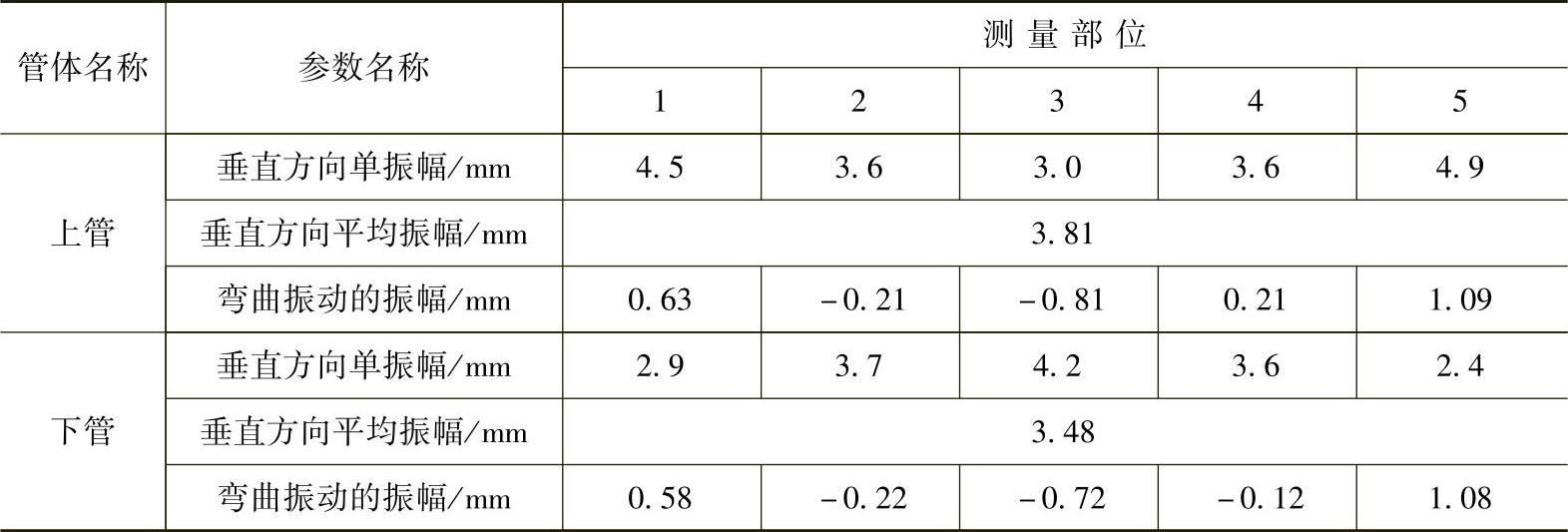
表8-6 双管振动输送机2的实测参数

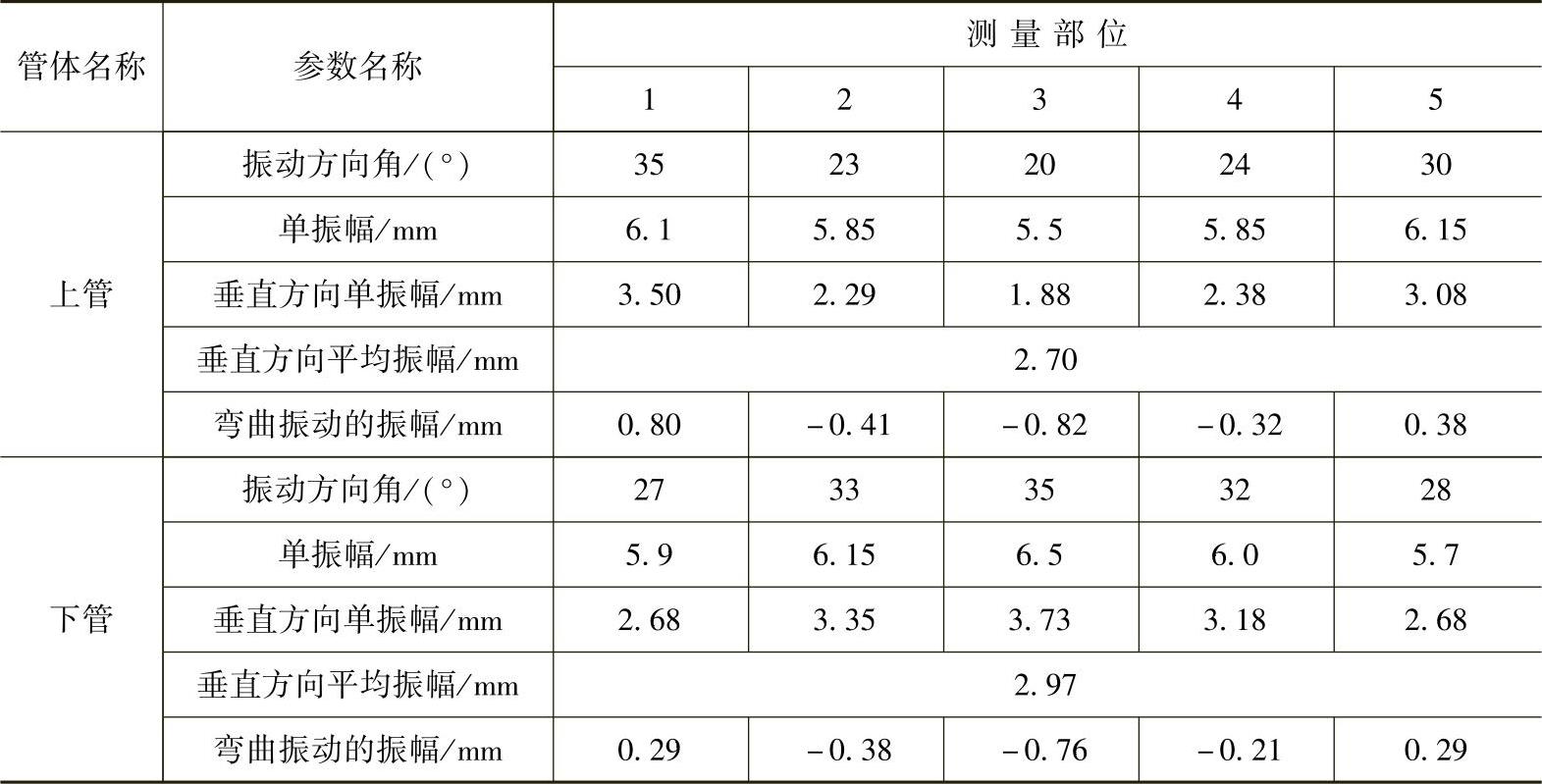
上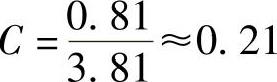管体 下管体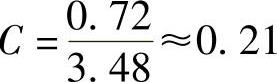

将另一双管振动输送机用振幅和振动方向角测得的数据列于表8-7。根据表8-5可求得弯曲振动系数C：

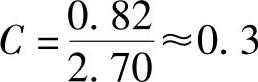上管体 下管体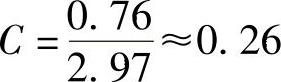

该振动输送机仍能完成物料输送任务，但槽体弯曲振动较为明显，对该机工作性能已有较大影响。