简谐激振力下的稳定响应分析

用上面的方法已经求得了前k阶固有频率和前k阶固有振型，由前k阶固有振型组成模态矩阵，就不难求出在简谐激振力作用下的前k阶稳态响应。

图8-24b所示系统的无阻尼受迫振动微分方程，显然具有如下形式：

式中 Y——各站的位移矢量；

M——质量矩阵，它是一个对角矩阵；

S——刚度矩阵；

Fτ——激振力幅值矢量；

θ——激振力的角频率。

设前k阶固有振型组成的模态矩阵为Y_M，它是n×k阶矩阵，把Y_M对质量矩阵归一化得到Y_N，它也是n×k阶矩阵，根据诸特征矢量对质量矩阵M和刚度矩阵S的正交关系，可以得到：

式中 S_P——上面求得的前k个特征值（即前k阶固有频率）组成的k×k阶对角矩

阵，S_P=diag[ω₁，ω₂，…，ω_k]；(www.xing528.com)

Y_P——正规坐标，Y_P=Y_N^TY；

F_τP——正规化了的激振力幅值列矢量，F_τP=Y^T_NF_τ=[q_P1，q_P2，…，q_Pk]^T。

由方程式（8-64）易于求得正规坐标下的稳态响应，再经过坐标变换，即可求在原坐标下的响应。

以上叙述了用传递矩阵方法计算振动输送机弯曲振动的固有频率、振型及在简谐激振力作用下的响应的基本原理。在编写计算程序时，应考虑如何防止计算结果溢出。

为了实现上述计算过程，我们用FORTRAN语言编制了EBVA程序，由于篇幅所限，这里不作引述。

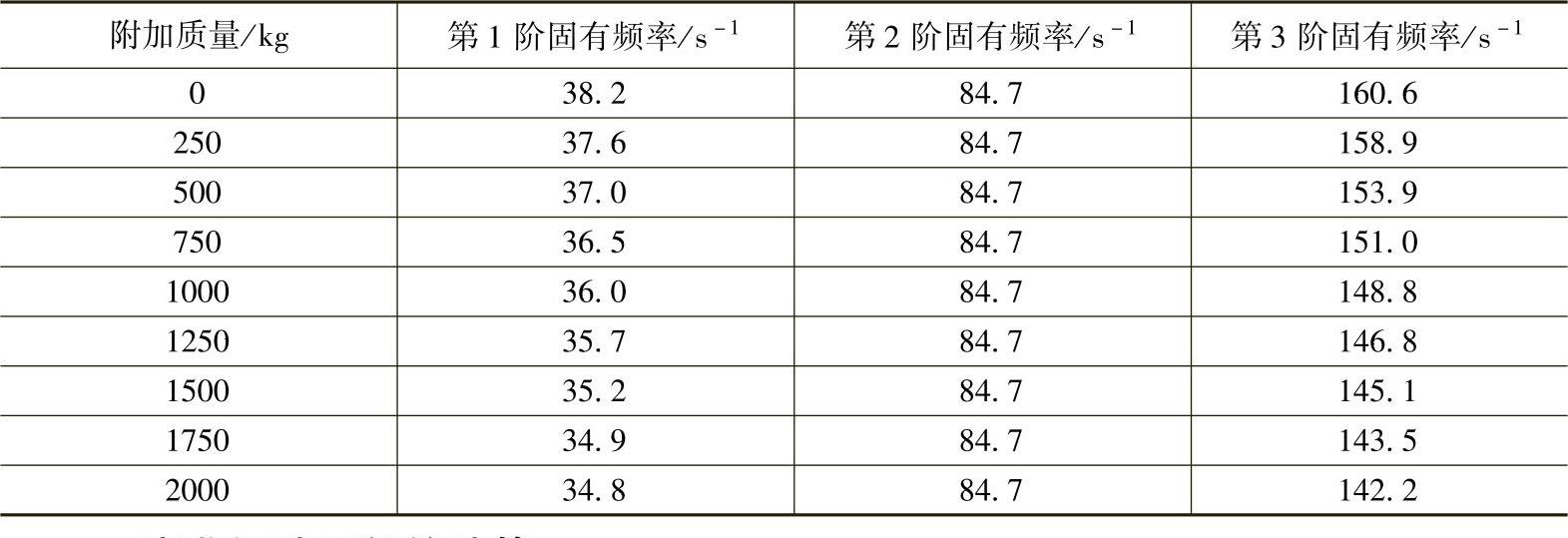
在某振动输送机的中间位置，每增加250kg的质量，即应用EBVA程序重复计算弯曲振动的固有频率，连续8次计算结果列于表8-4。由表可以看到，随着附加质量的增加，第1、第3阶固有频率逐渐减小，而第2阶固有频率则几乎不变。同时还可以看出，当附加质量为500kg时（占总质量的1/20），第1阶固有频率下降3.1%，第3阶固有频率下降8.2%。当附加质量为1000kg时（占总质量的1/10），第1阶固有频率下降5.8%，第3阶固有频率下降8.3%。可见附加质量不超过槽体质量的1/10时，把单质体振动输送机作为质量均匀分布的连续体，按文献中的公式，即

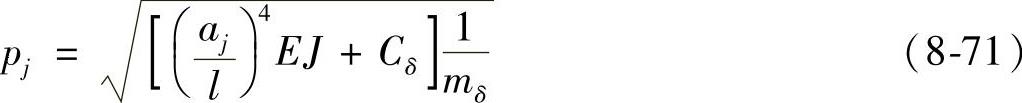
计算固有频率，一般不会造成很大的误差。

表8-4 弯曲振动固有频率的计算结果