求解弯曲振动固有频率的方法

弹簧隔振单质体振动输送机的机构简图如图8-20a所示，图8-20b为计算弯曲振动的力学模型。振动输送机经离散化后，可得到仅有质量而不占几何空间的站（质点）和仅有刚度而无质量的场（梁段）。这里把站的左边点记为L，右边点记为R（见图8-20b），各点的状态向量包括两个位移和两个与之相应的内力，即由挠度y和转角ψ，剪切力Fτ和弯矩M所组成，将其记作

令站的下标由1开始一直到n，而场的下标由2开始一直到n，同时把建立场两端状态矢量之间关系的矩阵叫做场矩阵，把建立站两端状态矢量之间关系的矩阵叫做点矩阵。

取第i个场进行研究（2≤i≤n），该场的受力状态如图8-21所示，图中各量的正、负号的规定与通常材料力学中的规定相同。槽体做自由振动时，该梁段所受的力应满足下列平衡条件：

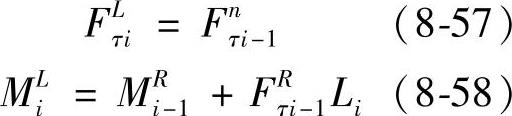
式中 L_i——第i段的长度。

为了求出两个位移，写出任一点x的弯矩公式为

对上式积分，便可得到转角与位移的公式

图8-20 弹簧隔振单质体振动输送机的机构简图

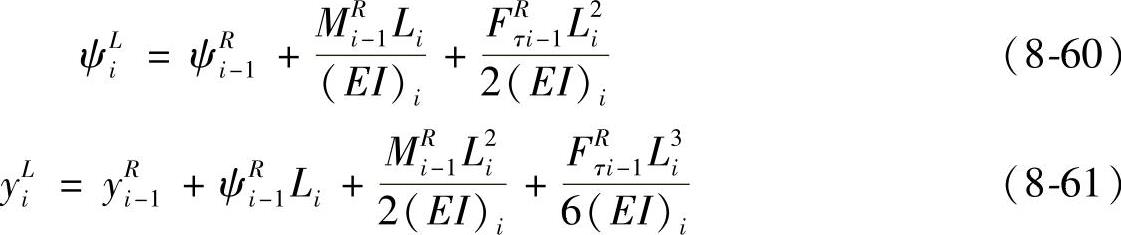
式中 （EI）i——场i的抗弯刚度。

把式（8-57）、式（8-58）、式（8-60）、式（8-61）写成矩阵形式，便有

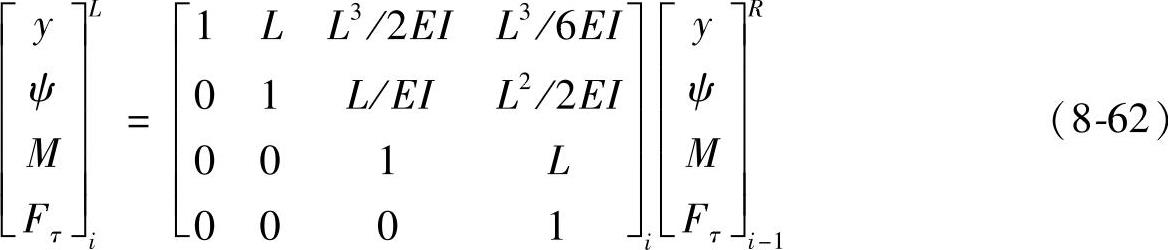
上式可简写为

式中 F_i——场矩阵。

图8-22表示第i站的受力状态，这是一个由无重弹簧支撑的站，站的质量为m_i，支撑弹簧刚度为k_i。当槽体做自由振动时，m_i以角频率ω和振幅y_i做简谐运动。根据达朗贝尔原理则有如下关系式：

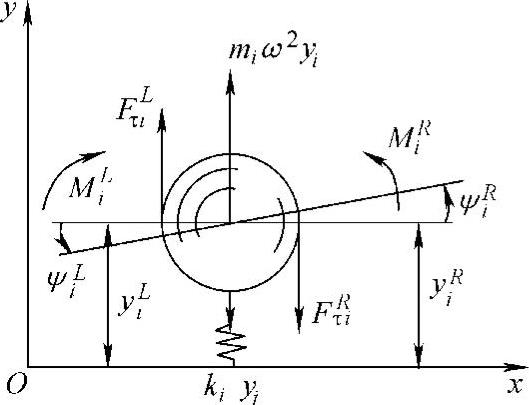
图8-21 场的受力状态图

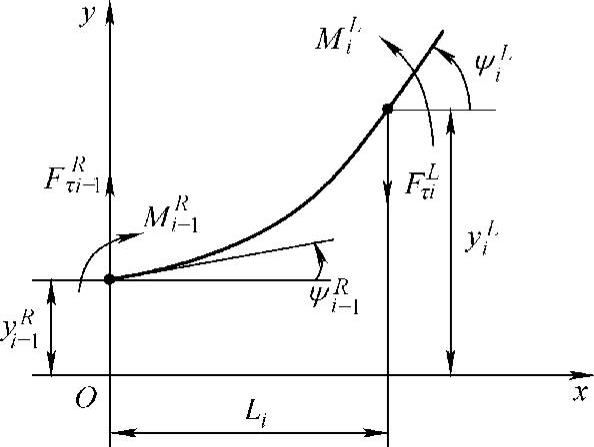
图8-22 第i站的受力状态图(www.xing528.com)

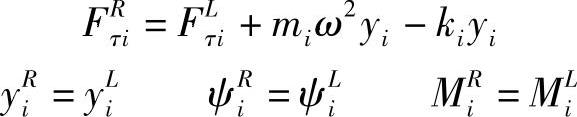
将上述关系式写成矩阵形式，便有

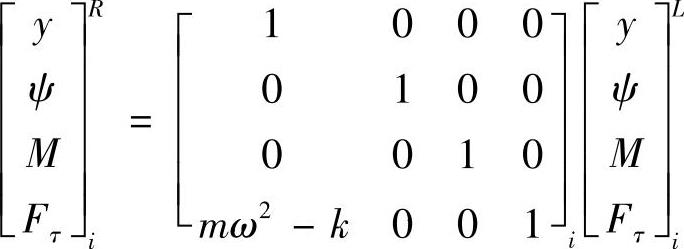
简写为

式中 P_i——第i站的点矩阵。

若该站不受外部约束，则应有k_i=0。根据场矩阵和点矩阵的定义，式（8-63）及式（8-64）可直接写出：

Z^R_n=P_nF_nP_n-1F_n-1…P₂F₂P₁Z^L₁=AZ^L₁ （8-65）

式中A——4×4阶方阵，称为传递矩阵，A=P_nF_nP_n-1F_n-1…P₂F₂P₁。

根据振动输送机的边界条件，两端为自由端或弹性支撑端，由式（8-60）可知：

式中，a₃₁、a₃₂、a₄₁、a₄₂为矩阵A的元素。由于y₁、ψ₁取任何值上式都应成立，所以必然有

这是一个终端判据，R是角频率ω的多项式，显然能够满足式（8-67）的ω值，就是振动输送机弯曲振动的固有频率。因此求弯曲振动固有频率的问题，就归结为求方程（8-67）的根。为了求解方程（8-67），本节采用了半步长自动觅根方法。由于振动输送机弯曲振动的固有频率，较一般轴的固有频率低得多（振动输送机的抗弯刚度与其长度之比EI/L较普通轴为小），并且通常只需求最低的几阶固有频率，因此弯曲振动固有频率的求解适合采用这种方法。求解方程（8-67），即R（ω）=0的根，可以分下面两个步骤进行。

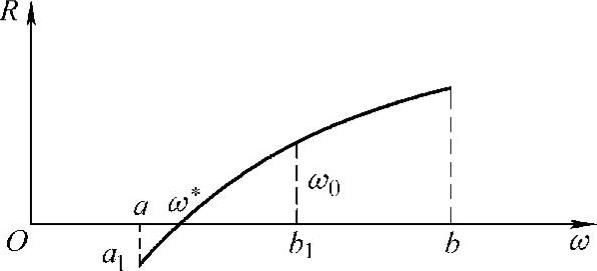
图8-23 半步长自动觅根法

（1）求根的初始近似值 首先选定一个初始值，例如ω=d（d≥0），然后由此初值出发，按某个预选的步长h一步一步地递增（向右移动），并检查每一步的起点ω_a和终点ω_a+h对应的函数R（ω）值是否同号，如果发现R（ω_a）和R（ω_a+h）为异号，即

R（ω_a）R（ω_a+h）<0则所求的根必在ω_a与ω_a+h之间，于是便可转入自动觅根过程。

（2）求误差小于允许值的根的近似值 设方程R（ω）=0在有根区间内仅有一个根ω∗，取区间中点ω₀，并检查R（a）和R（ω₀）是否同号。若同号，则ω^∗在ω₀和b之间；若异号，则ω^∗在a和ω₀之间。于是便得到新的区间（a₁，b₁），如图8-23所示，如此继续下去便得到ω₀、ω₁、ω₂……序列，其极限即为ω∗，若取ω_k为根的近似值，则

ε=b_k+1-a_k+1

求得第一个根之后，在此根的基础上继续按预定步长向右搜索，重复上述两个

过程，即可求得其余诸根。