根据工艺要求，物料沿振动离心机（见图8-7）锥体的内壁作间歇的正向滑动，实现离心脱水并自动排料，在这种机器中不会出现反向滑动或跳动。物料在一个运动周期内的运动状态和力学模型如图8-8、图8-9所示[1]。在滑动区间内，物料作用在锥体上的力为正向滑动摩擦力和惯性力分量之和，在间歇区间内，物料与锥体之间相对静止，只有惯性力分量。
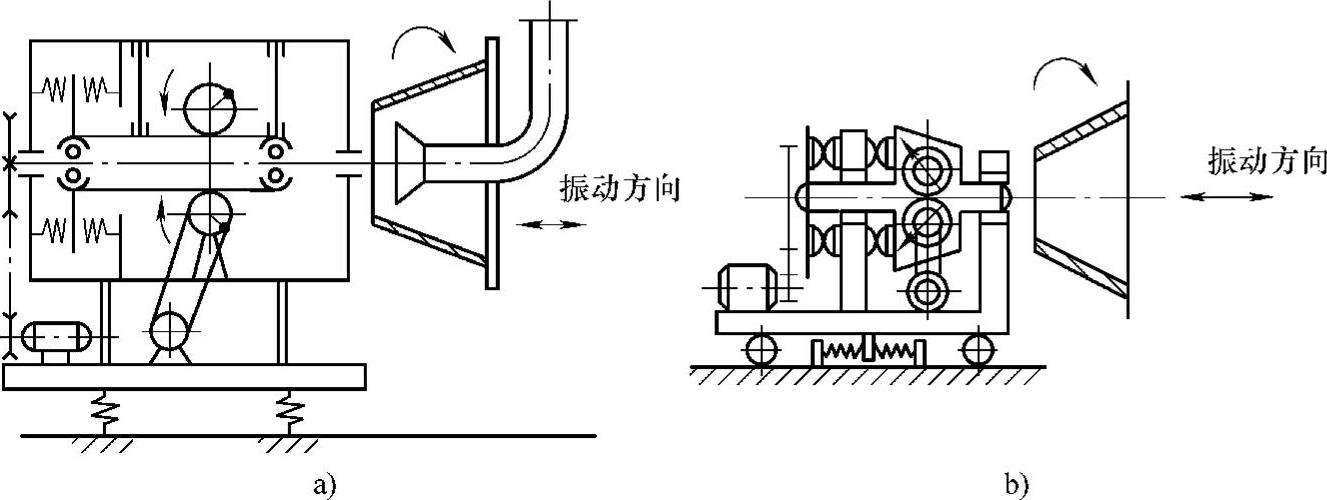
图8-7 振动离心脱水机的工作机构示意图
a）对称式 b）不对称式
设φk为物料的滑始角，φm为物料的滑止角，可以推出，在一个周期内物料的非线性惯性力可写成如下分段线性方程：
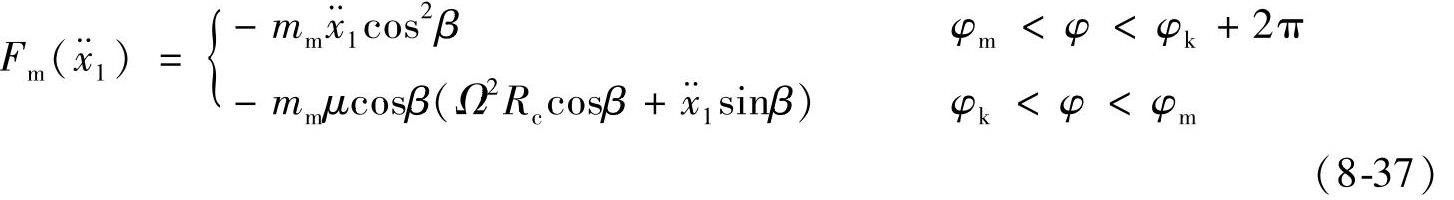
式中 mm——锥体中物料的质量（kg）；
β——锥体锥角的一半（°）；
Rc——物料在锥体中的当量半径（m）；
Ω——锥体回转角速度（rad/s）；
μ——物料滑动摩擦系数。
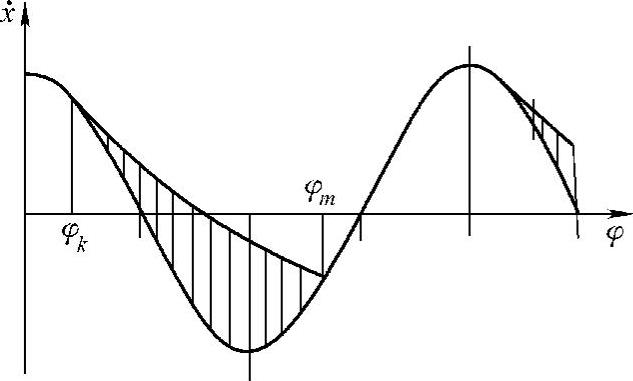
图8-8 一个运动周期内物料的单向滑动运动
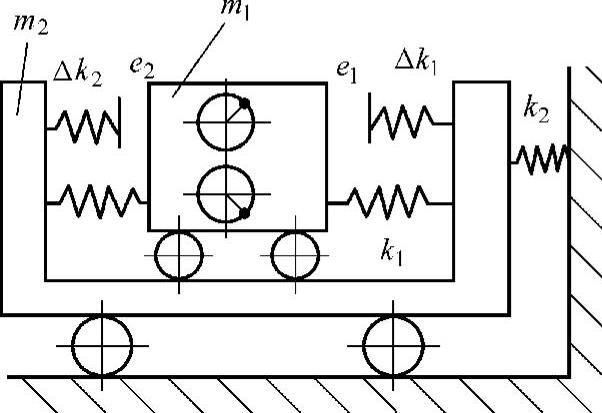
图8-9 不对称振动离心机的力学模型
以不对称分段线性刚度的振动离心机为研究对象进行分析，其简化力学模型如图8-9所示。
考虑物料的非线性惯性力，并以小参数标记，其运动方程可以写成如下两自由度形式：
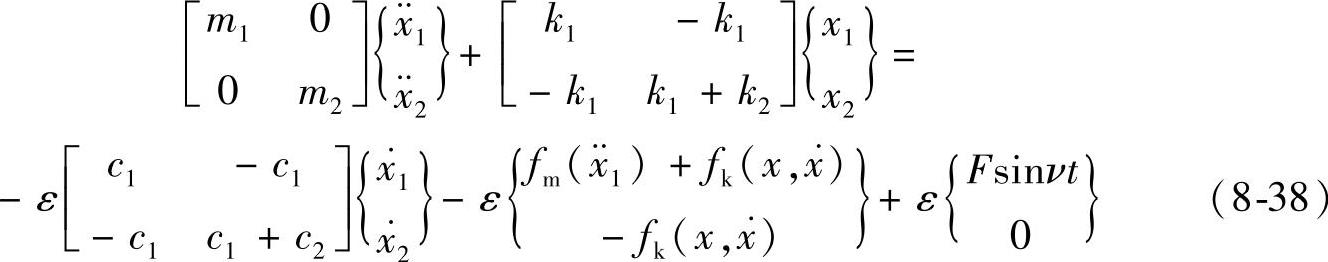
式中 x1，x2，x——质体1和质体2的位移、两者的相对位移，x=x1-x2；
m1，m2——质量1和质量2，质量1中还包含物料等效质量：m1=m1′+mmsin2β（m1′为质体1的质量）；
k1，k2，c1，c2———质体1与质体2之间的弹簧在水平方向的刚度、质体2与基座之间的弹簧刚度以及相应的粘性阻尼系数；
F——偏心块产生的激振力，F=m0ν2r，其中m0为偏心块质量，r为偏心距；
ν——偏心块回转角速度；
fk（x，ẋ）——质体1和质体2之间的不对称非线性弹性恢复力：
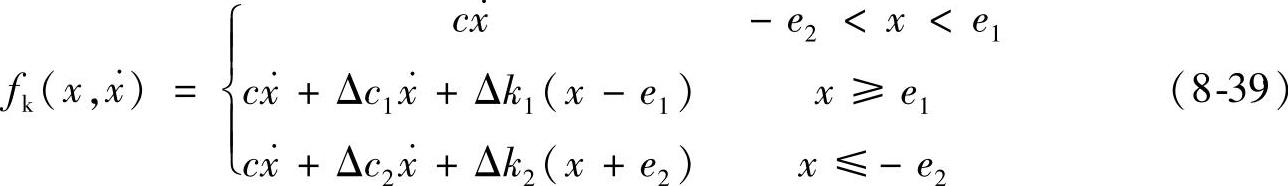
c——与线性弹簧k1有关的阻尼系数；
Δk1、Δk2——左右间隙弹簧刚度；
Δc1、Δc2——与间隙弹簧有关的阻尼系数；
e1、e2——左右间隙。
2.振动离心脱水机的非线性振动响应
振动离心脱水机通常在第二固有频率ω2的邻近工作。设系统不存在内共振，只分析以ω2为基频的振动，高频成分视为小项，这与工程实际需要相吻合。
根据系统的派生方程，可求得固有频率ω1、ω2以及相应的振型矩阵Φk：
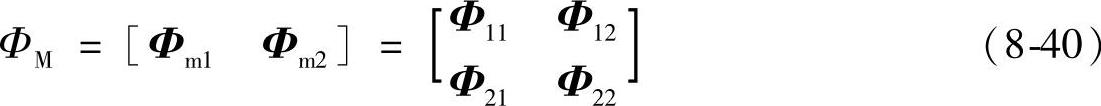
其中
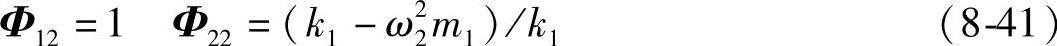
第二主质量和主刚度分别为(www.xing528.com)
M2=ΦTm2MΦm2K2=ΦTm2KΦm2（8-42）
下面对第二主振动的单频振动进行分析，即
这样，在第二主坐标上的运动方程为
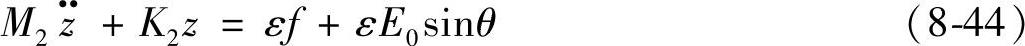
其中，非线性项可以整理为
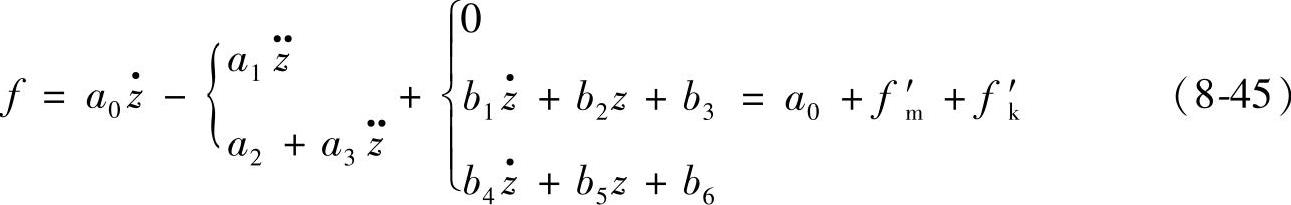
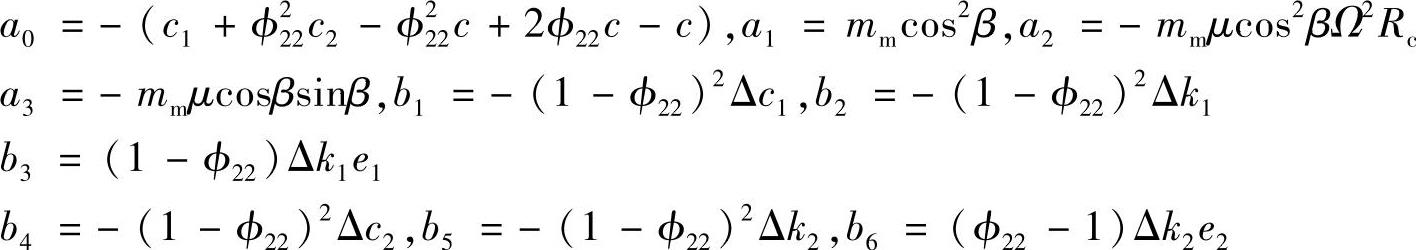
并设z的一次近似解为
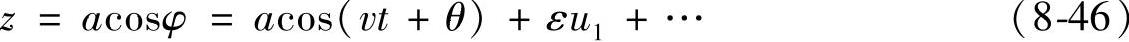
在一次近似情况下，设φ1=arccos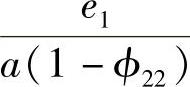
，为第一象限角；φ1=
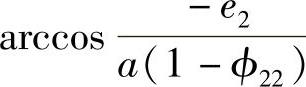，为第二象限角。等效阻尼系数和等效刚度分别是
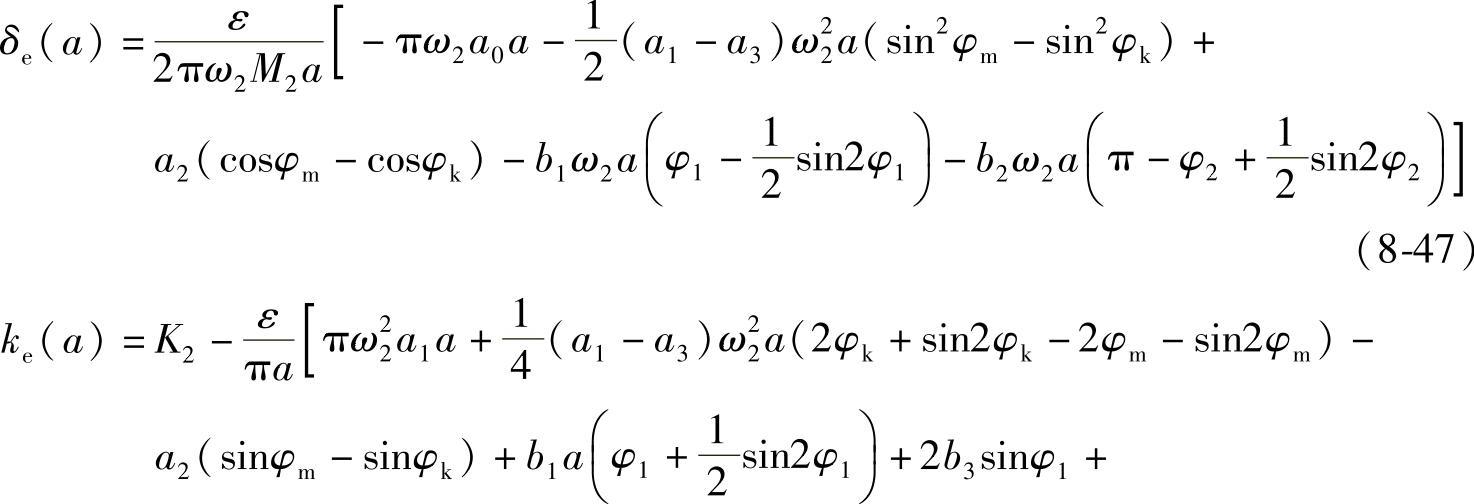
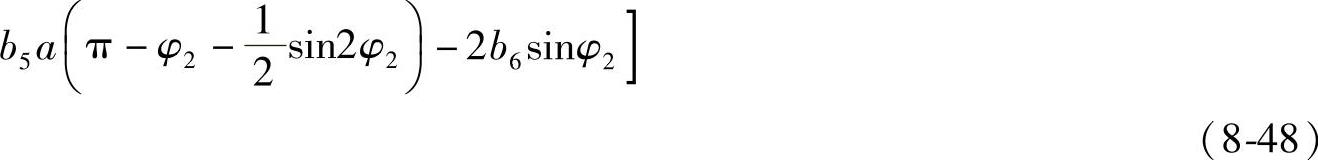
等效固有频率为
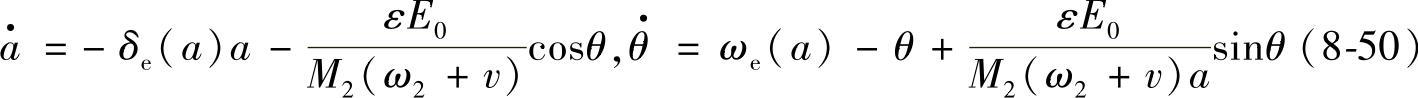
对于工程上关心的定常状态，由a·=0，θ·=0得到频率响应方程为
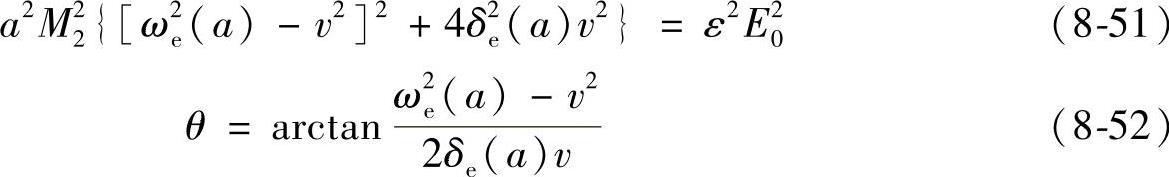
做进一步推导，可以求得包含二、三次谐波成分的修正项如下：
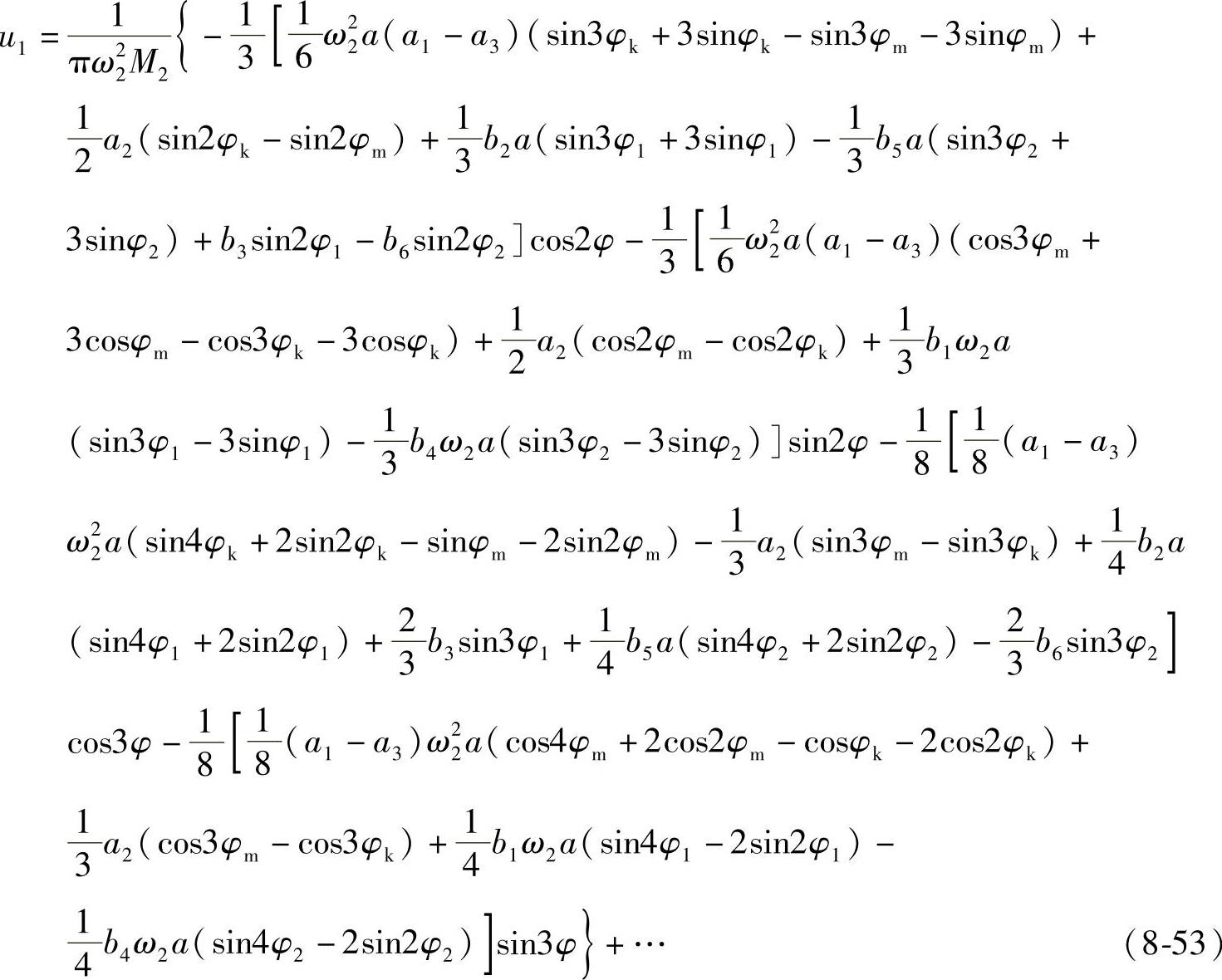
3.振动离心脱水机的幅频特性
从以上结果可以看出，非线性弹簧和物料对系统的等效刚度和等效阻尼系数均有直接影响，从而影响系统的振幅和相位差角。图8-10为振动离心脱水机的振动系统频率响应曲线和高次谐波频率响应曲线。图8-10a中是取不同物料质量时（mm，2mm）的主共振曲线（a0为名义幅）；图8-10b是不同锥体回转角速度（Ω，5Ω，8Ω）的主共振曲线；图8-10c和图8-10d是物料质量不同和锥体回转角速度不同时，二次和三次谐波共振曲线，其中A2，A3是相应的二次和三次谐波项的正弦与余弦项的合成。
4.振动离心脱水机的试验振动响应
利用加速度传感器直接测得振动离心脱水机的筛篮沿轴向的振动加速度，所得加速度曲线如图8-11所示。由图可以看出，不对称振动离心脱水机加速度曲线有明显的不对称特征，而对称振动离心脱水机的加速度曲线是对称的。两条曲线都有明显的非线性特征。
由上述分析可得到如下结论：
1）物料非线性惯性力对主共振曲线有影响，物料质量增大，曲线将向左侧偏移，呈现硬式特征。锥体回转角速度Ω对系统的主共振曲线也有影响，随着Ω的增加，曲线向右侧产生偏移。
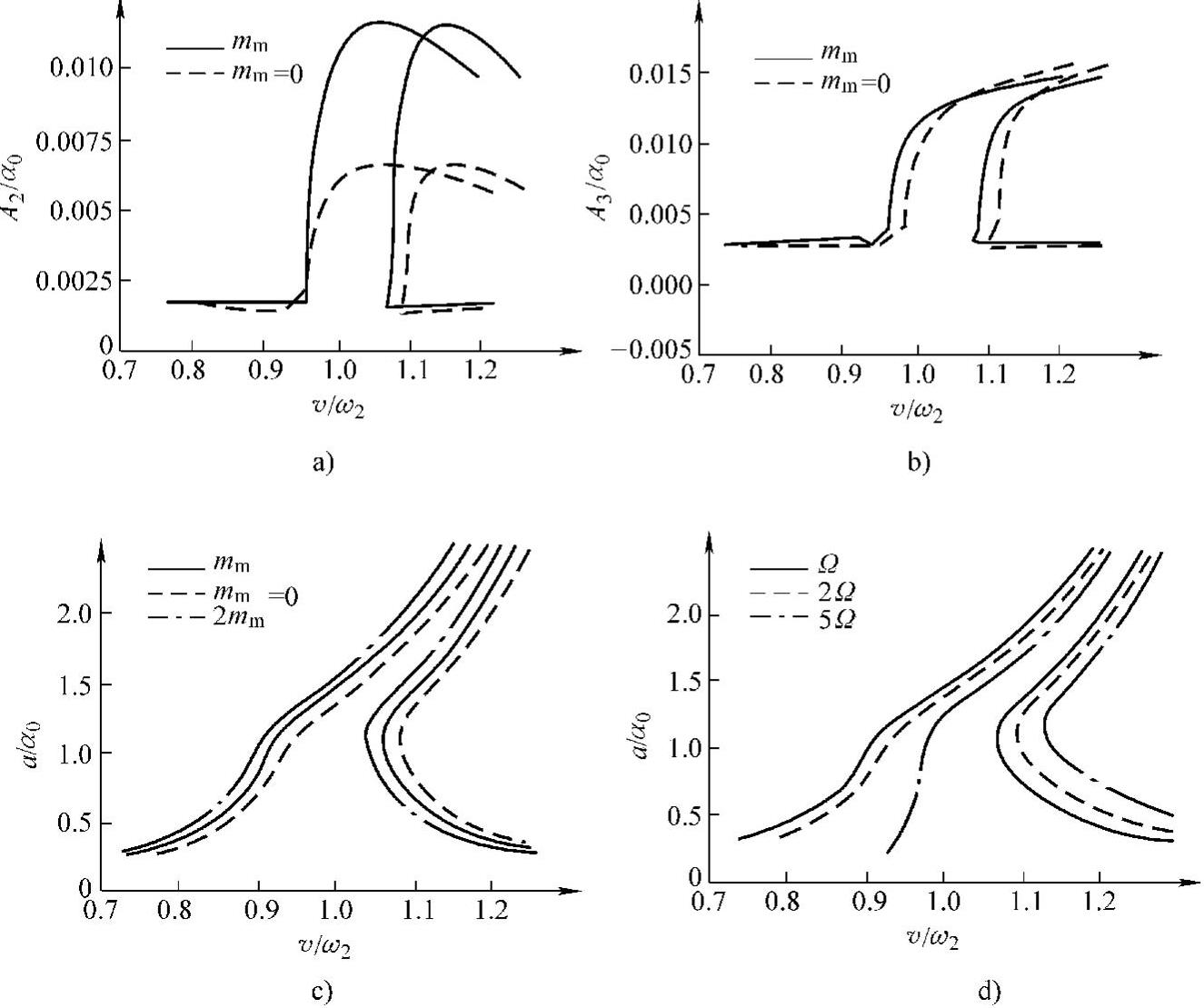
图8-10 振动离心脱水机的幅频特性曲线
a）物料质量不同时的基波 b）锥体转速不同时的基波 c）有无非线性惯性力的二次谐波 d）有无非线性惯性力的三次谐波
2）物料非线性惯性力同时还影响振动系统的二、三次等高次谐波成分（见图8-10c和图8-10d）。由于高次谐波的存在，会导致较大的振动加速度，应给予足够的重视。例如，当某些零部件的固有频率与这些高次谐波成分的频率接近时，可能会产生共振，使其动应力增大。在设计时，最好使它们的固有频率为工作频率的5倍以上。
上述结果亦可对其他具有类似的非线性弹性力和非线性惯性力的振动机械（如近共振筛等）的设计提供理论依据和分析方法。
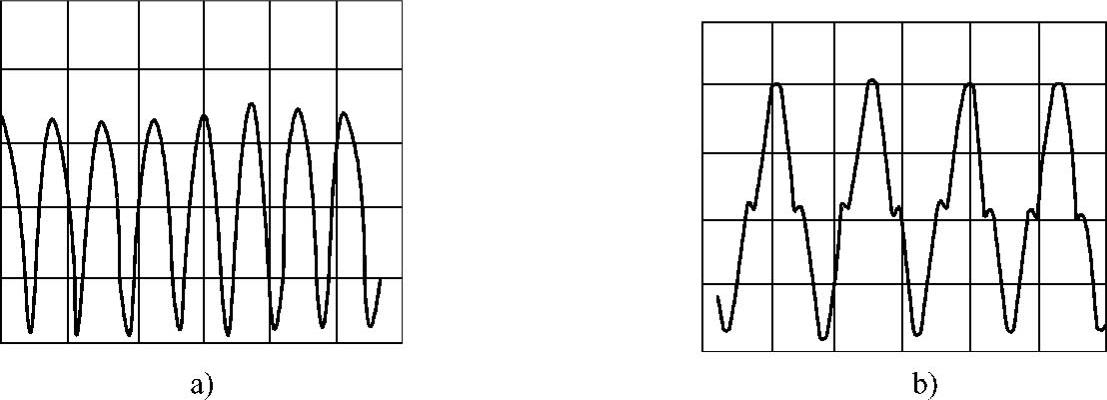
图8-11 振动离心脱水机的试验加速度曲线
a）不对称式 b）对称式
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
