机械系统线性或非线性动力学建模优化

各类振动系统的建模可以采用不同的方法，也可以采用相似的方法。

（1）建立一般线性或非线性振动系统动力学方程的方法

1）按牛顿定律建立方程。取任何一分离体，该分离体的惯性力等于其他作用力之和，即

∑m_ii=∑F_n （8-1）

式中 m_i——分离体中的第i个质量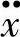；_i——分离体第i个质量的加速度；

F_n——作用于该分离体上的第n个外力。

在前面介绍的各章中，广泛采用了这一方法。

2）按达伦培尔原理建立方程。按照这一原理，作用于某一独立系统的所有作用力F_i之和等于零，包括系统中的惯性力，即

∑F_i=0 （8-2）

3）按拉格朗日方程建立动力学方程。依据机器的力学模型图，写出系统的动能T、势能V及能量耗散函数D，再按照拉格朗日方程进行运算，即可求出各个广义坐标上的运动微分方程式

式中 q_i、——广义坐标和广义速度；

F_qi——广义力。(www.xing528.com)

由上述方程第一项，可求出系统的惯性力，第三项为弹性力，第四项为阻尼力。本章第8.5节将介绍按照拉格朗日方程建立动力学方程的方法。

（2）轴类零件或大长度槽体按传递矩阵法建立动力学方程 本章第8.8节将对传递矩阵法做较详细的说明，并用此法计算长距离振动输送机弯曲振动的固有频率和在简谐激振力作用下的稳态响应。

传递矩阵法可用来计算长距离振动输送槽体的弯曲振动的固有频率与响应，以及轴类零件弯曲振动的固有频率与响应等。

（3）机器结构或框架用线性或非线性弹性力学有限元法建立动力学方程 用弹性力学有限元法建立方程，主要是基于弹性力学的变分原理，如虚位移原理、瞬时最小势能原理等。用有限元法建立动力学方程的步骤如下：

1）将系统划分若干有限单元，选取单元坐标系。计算在总坐标系中单元的惯性矩阵、阻尼矩阵、刚度矩阵和节点力列阵，即

m_s，c_s，k_s及f_s（s=1，2，…，r）

单元的动力学方程为

2）确定系统位移坐标向量U及各单元的变换矩阵A_s，进而计算系统的惯性矩阵M、阻尼矩阵C、刚度矩阵K和节点力列阵F，即

3）建立结构总体坐标系下的运动微分方程式：

然后按照方程求系统的固有频率、振型和动力响应。