计算装配尺寸链的方法和原理

在确定了装配尺寸链的组成之后，就可以进行具体的分析计算工作。装配尺寸链的计算方法与装配方法密切相关，同一项装配精度，采用不同的装配方法时，其装配尺寸链的计算方法也不相同。

装配尺寸链的计算是在产品设计过程中进行的，多采用反计算法，而正计算法仅用于验算。反计算即已知装配精度（封闭环）的公称尺寸及其偏差，求解与该项装配精度有关的各零部件（组成环）的公称尺寸及其偏差。

计算装配尺寸链的公式可分为极值法和概率法。概率法仅适用于大批量生产的装配尺寸链计算；而极值法可用于各种生产类型的装配尺寸链计算。

1．装配尺寸链的极值解法

在装配尺寸链中，一般各组成环的公称尺寸是已知的，在计算时仅对其进行验算。所以，计算装配尺寸链主要是如何将封闭环的公差合理地分配成各组成环的公差。

按极值法解算装配尺寸链的公式与工艺尺寸链的计算公式相同，这里不再赘述。

采用极值法解算装配尺寸链时，为保证装配精度要求，应确保各组成环公差之和小于或等于封闭环公差，但为了使各组成环公差尽可能大，在计算时取等号，即

对于线性尺寸链，则

式中　T0—封闭环公差；

Ti—第i 个组成环的公差；

ξi—第i 个组成环的传递系数；

m—组成环的环数。

在按极值法计算装配尺寸链时，可按以下步骤进行。

1）首先校核封闭环尺寸是否正确：

2）按等公差原则，计算各组成环平均公差：

当装配尺寸链中有q 个组成环的公差已经确定时（组成环是标准件或已在别的装配尺寸链中先行确定），其余组成环的平均公差计算公式为

3）根据各组成环公称尺寸的大小和加工时的难易程度，对各组成环的公差进行适当的调整。在调整过程中应遵循以下原则：

① 组成环是标准件尺寸时（如轴承环的宽度或弹性挡圈的厚度等），其公差值及其分布在相应标准中已有规定，为已定值。

② 当组成环是几个尺寸链的公共环时，其公差值及其分布由对其要求最严的尺寸链先行确定，对其余尺寸链则也为已定值。

③ 尺寸相近、加工方法相同的组成环，其公差值相等。

④ 难加工或难测量的组成环，其公差可适当加大；易加工、易测量的组成环，其公差可取较小值。各组成环的公差值尽量取成标准值，各组成环的公差等级尽量相近。

⑤ 选一组成环作为协调环，按尺寸链公式最后确定。协调环应选择易于加工、易于测量的组成环，但不能选择标准件或已经在其他尺寸链中确定了公差及其偏差的组成环作为协调环。

⑥ 确定各组成环的极限偏差，对于属于外尺寸的组成环（如轴的直径）按基轴制（h）确定其极限偏差；对于属于内尺寸的组成环（如孔的直径）按基孔制（H）确定其极限偏差，协调环的极限偏差按公式计算确定。

2．装配尺寸链的概率解法

用极值解法时，封闭环的极限尺寸是按组成环的极限尺寸来计算的，而封闭环公差与组成环公差之间的关系是式（7-1）来计算的。显然，此时各零件具有完全的互换性，机器的使用要求能得到充分的保证。但是，当封闭环精度要求较高，而组成环数目又较多时，由于各环公差大小的分配必须满足式（7-1）的要求，故各组成环的公差值Ti必将取得很小，从而导致加工困难，制造成本增加。生产实践表明，一批零件加工时其尺寸处于公差带范围的中间部分的零件占多数，接近两端极限尺寸的零件占极少数。至于一批部件在装配时（特别是对于多环尺寸链的装配），同一部件的各组成环，恰好都是接近极值尺寸的，这种情况就更为罕见。这时，如按极值解法求算零件尺寸公差，则显然是不经济的。但如按概率法来进行计算，就能扩大零件公差，且便于加工。

装配尺寸链的组成环是有关零件的加工尺寸或相对位置精度，显然，各零件加工尺寸的数值是彼此独立的随机变量，因此作为各组成环合成量的封闭环的数值也是一个随机变量。由概率理论可知，在分析随机变量时，必须了解其误差分布曲线的性质和分散范围的大小，同时还应了解尺寸聚集中心（即算术平均值）的分布位置。

（1）各环公差值的计算

由概率论可知，各独立随机变量（装配尺寸链的组成环）的均方根偏差σi与这些随机变量之和（尺寸链的封闭环）的均方根偏差σ0之间的关系为

但由于解算尺寸链时是以误差量或公差量之间的关系来计算的，因此上述公式还需要转化成所需要的形式。(www.xing528.com)

正如在加工误差的统计分析中已介绍过的那样，当零件加工尺寸服从正态分布时，其尺寸误差分散范围 ωi与均方根偏差 σi之间的关系为

当零件尺寸分布不为正态分布时，需引入一个相对分布系数 ki，因此有

相对分布系数 ki表明了所研究的尺寸分布曲线的不同分散性质（即曲线的不同形状），并取正态分布曲线作为比较的根据（正态分布曲线的 ki值为1）。各种 ki值可参见第4章表4-5。

尺寸链中如果不存在公差数值比其余各组成环公差大得很多，且尺寸分布又偏离于正态分布很大的组成环的情况，则不论各组成环的尺寸为何种分布曲线，只要组成环的数目足够多，则封闭环的分布曲线通常总是趋近于正态分布的，即 k0≈ 1。一般来说，组成环环数不少于5 个时，封闭环的尺寸分布都趋近于正态分布。

此外，在尺寸分散范围 ωi恰好等于公差 Ti的条件下，就得到尺寸链计算的一个常用公式：

只有在各组成环都是正态分布的情况下，才有

又若各组成环公差相等，即令时，则可得各环平均公差 Tav为

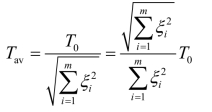
当装配尺寸链为直线尺寸链时，有

与用极值法求得的组成环平均公差比较，概率解法可将组成环平均公差扩大倍。但实际上，由于各组成环的尺寸分布曲线不一定是按正态分布的，即 ki大于1，所以实际扩大的倍数小于

用概率解法之所以能够扩大公差，是因为在确定封闭环正态分布曲线的尺寸分散范围时假定 ω0=6σ0，而这时部件装配后在 T0=6σ0范围内的数量可占总数的99.73%，只有0.27%的部件装配后不合格。这样做在生产上仍是经济的。因此，这个不合格率常常可忽略不计，只有在必要时才通过调换个别组件或零件来解决废品问题。

（2）各环公称尺寸和中间偏差的计算

根据概率论，封闭环的算术平均值等于各组成环算术平均值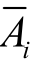的代数和，即

当各组成环的尺寸分布曲线均属于对称分布，而且分布中心与公差带中心重合时，算术平均值即算术平均值等于公称尺寸与中间偏差之和。因此，上式可以分为以下两式：

此时的计算公式与极值解法时所用相应计算公式完全一致。

当组成环的尺寸分布属于非对称分布时，算术平均值相对于公差带中心的尺寸即平均尺寸就有一偏移量，此偏移量可用表示（图7-4）。这时：

显然，在T 为定值的条件下，偏移量越大，α 也越大，可见α 可用来说明尺寸分布的不对称程度。因而α 即称为相对不对称系数，一些尺寸分布曲线的α 值可参见第4章表4-5。

由于多数情况下封闭环为正态分布，所以当某些组成环为偏态分布时，其公称尺寸计算公式不变，而中间偏差计算公式为

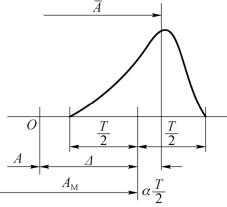
图7-4　不对称分布时的尺寸计算关系

（3）概率解法时的近似估算法

对概率解法进行准确计算时，需要知道各组成环的误差分布情况（ Ti、ki及 αi值）。如有现场统计资料或成熟的经验统计数据，便可据之进行准确计算。而在通常缺乏这种资料或不能预先确定零件的加工条件时，便只能假定一些 ki及 αi值进行近似估算。

这一方法是以假定各环的尺寸分布曲线均对称分布于公差带的全部范围内，即αi= 0，并取平均相对分布系数kav来作近似估算的。至于kav的具体数值，有的资料建议在1.2～1.7范围内选取；有的资料则在一定的统计试验基础上，建议采用kav=1.5的经验数据。

这样，对直线尺寸链整个计算只用到两个简化公式：

但必须指出，在采用概率近似算法时，要求尺寸链中组成环的数目不能太少。