移相键控技术及其在相干解调中的应用

移相键控(Phase Shift Keying,PSK)利用载波信号的不同相位去传输数字信号的1码和0码,是数字调制方式常用的一种。

1.二相绝对移相键控

绝对移相键控是移相键控的一种,二相绝对移相键控通常记作2PSK。

(1)移相只改变载波信号的相位,即不同的基带码对应的载波起始相位不同。在图6.25中,载波起始相位与基带码的关系如下:载波0相位对应基带信号的1码即1→0*;载波π相位对应基带信号的0码,即0→180*(π)。或反之,1→180*(π),0→0*。

(2)2PSK调制的原理框图如图6.25(a)所示,而2PSK信号工作过程波形如图6.25(b)所示。

图6.25 2PSK产生过程

图6.25(b)所示的波形相乘结果验证了载波起始相位与基带码所定义的规则。其中相乘器的具体典型电路(又称倒接开关调制器)如图6.26所示。

图6.26 2PSK信号的调制电路

倒接开关调制器的工作过程是,1码发正脉冲,A点电位高于B点电位,使上、下一对二极管导通,载波cosωc t正向输出,已调波相位为0*。如果0码发负脉冲,A点电位低于B点电位,使交叉的一对二极管导通,输出e(t)=-cosωc t=cos(ωc t+180°),即载波反向输出,则实现了“1→0*”和“0→180*(π)”的规则,而如果B点是1码正脉冲,B点电位高于A点电位,则实现“1→180*(π)”和“0→0*”的规则。

(3)2PSK信号的相干解调框图和解调工作波形分别如图6.27(a)和如图6.27(b)所示。

(4)2PSK信号是以一个同定初相的未调载波为参数的,因此,解调时必须有与此同频同相的同步载波。如果同步不完善,是存在相位误差,造成误判,这种现象称为相干载波的相位模糊。例如,本地载波反相180*即为cos(ωc t+180*),称为倒π现象。解调后经判决得到的1码、0码,它们与图6.27示出的结果将完全相反,造成严重的错码,其产生过程如图6-28所示。

图6.27 相干解调法框图与工作波形

图6.28 倒π现象的产生过程

为克服由于相干载波的相位模糊现象而造成的严重误码,目前在调制方式中,不采用2PSK信号,而采用差分(相对)移相键控(Differential Phase Shift Keying,DPSK)信号。根据差分(相对)移相信号本身的特点,相干载波即使发生倒π现象也不会使解调输出的基带信号发生误码。

2.二相差分移相键控

差分移相键控或称为相对移相键控,是为了克服相位模糊现象,利用调制信号前后码元之间的载波相位的相对变化来传递信息。通常二相数字绝对移相键控通常记作2DPSK。

①差分码(相对码)若相对于前一码元电平有变化(即不同),则用1表示;如果无变化(即相同),则用0表示。由绝对码变成相对码的例子如图6.29所示。由于初始参数电平有两种可能,因此有图6.29所示的两种波形。

图6.29 绝对码变成相对码的例子

绝对码与相对码(或称为差分码)的互相转换电路实现方法就是使用模2加法器和延迟器(延迟一个码元宽度Tb)。绝对码变成相对码的过程称为差分编码,相对码变成绝对码的过程称为差分译码,如图6.30所示。

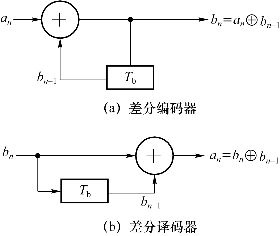
图6.30 绝对码与相对码的互相转换

图6.30(a)所示的差分编码的逻辑关系:本时刻的差分码bn(相对码)等于本时刻的绝对码an模2加本时刻经延迟1 bit的bn-1。若设发送端的绝对码序列为{ai},信道传输的相对码序列为{bi},则有

差分解码的逻辑为

二相相对移相键控规则及波形实现方法如下:每一码元发出的载波相位取决于前一码元的载波相位,发1码时,发出的载波相位比前一码元的载波相位改变180°,发0码时,发出的载波相位与前一码元的载波相位相同,不估改变。即

2DPSK的波形如图6.31所示。

图6.31 2DPSK波形图

2DPSK调制框图及工作过程如图6.32所示。

图6.32 2DPSK产生过程

①2DPSK解调框图及工作过程如图6.33所示。

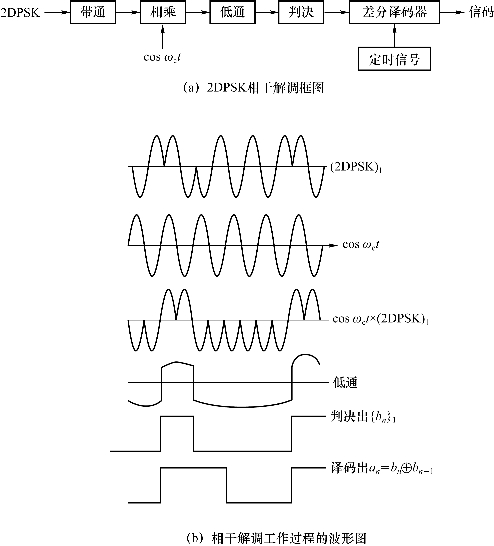
图6.33 2DPSK相干解调

②2DPSK相位比较法解调框图及工作过程如图6.34所示。

图6.34 2DPSK相位比较法解调

这种方法不需要码变换器(差分译码器),也不需要相干载波发生器,使用设备简单。其中,Tb延迟电路的输出起着参数载波的作用,乘法器起着相位比较(鉴相)作用。

判决器的判决准则:若抽样值x＞0,则判为0;若抽样值x＜0,则判为1。这种解调电路的前提条件是在接收2DPSK信号时不存在相位模糊问题。

下面介绍2DPSK解调如何解决相位模糊问题。在相干解调时,当接收的相干载波与本地载波不一致而产生倒相时,最终输出由bn变成但利用差分译码器的功能bn⊕bn-1=an,在bn反向后,仍然能使等式an成立,因此即使相干载波倒相,2DPSK解调器仍可正常工作,2DPSK解调器的工作过程如图6.35所示。

图6.35 2DPSK解决相位倒相问题的过程

3.2PSK和2DPSK的频谱

2PSK(或2DPSK)的一个信号C分解为两个振幅的通断键链控信号,如图6.36所示。A是1码发出的载波,为OOK信号A,B是0码发出的载波,为OOK信号B,显然C=A+B。

图6.36 2PSK或2DPSK信号分解

由此可见,2PSK(或2DPSK)信号是由两个2ASK信号叠加而成的,故2PSK(或2DPSK)频带宽带和2ASK信号频带一样,主要有两个边带。但是2PSK(或2DPSK)不像2ASK那样属于线性调制,它属于非线性调制,即由于两个分解信号的相位频谱不同,合成的2PSK(或2DPSK)信号的频谱形状与单独分解信号的频谱形状不同,也与基带信号频谱形状不同。

若信号C加上一个相位0°的连续载波信号D,将使2ASK信号幅度加倍,从而成为E,而使2ASK信号B得以抵消,即C+D=E,如图6.37所示。

图6.37 信号C和信号D的叠加

如图6.37所示,E频谱就是C频谱和D频谱的叠加结果(即C+D=E),其中D只是一条谱线,可以直接叠加在C频谱上。信号C和信号D叠加后得到的频谱图如图6.38所示,所以C频谱与E频谱的带宽一致。

图6.38 信号E的频谱图

综合分析以上两种情况,故得2PSK或2DPSK的频带为

【例6.1】 已知数字信息{an}=1011010,分别画出在以下两种情况下的2PSK和2DPSK波形。

(1)码元速率为1 200 baud,载波频率为1 200 Hz。

(2)码元速率为1 200 baud,载波频率为2 400 Hz。

解:(1)

Tc=

此时2PSK和2DPSK的波形如图6.39所示。

图6.39 波形图1

(2)Tb=

Tc=s

Tb=2Tc

此时,2PSK和2DPSK的波形如图6.40所示。

图6.40 波形图2

4.四相绝对移相键控(4PSK或QPSK)

(1)正交调制的概念

用向量表示正弦波,如u1=12sin(ωc t+),u1=12sin(ωc t-135°),由这二个式子画出的矢量表示如图6.41所示。

图6.41 向量图

在图6.22所示的基带信号中,若S(t)为周期方波,则S(t)即可展成式(6.6),其中Ω=2πfb=2π,Tb为一个码元时间,Ω≪ωc。

正交调制和解调电路如图6.42所示。调制器可用倒接开关调制器。

图6.42 调制和解调框图

S(t)中直流分量不能通过倒接开关调制器,故S(t)写成

现在我们以S(t)中的项作为输入,如图6.43所示。

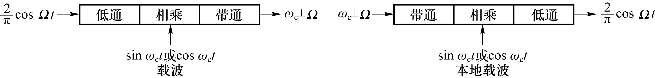
图6.43 cosΩt通过调制和解调电路

为简化起见项看成cosΩt,载波用cosωc t。发送端的表达式为

接收端的表达式分为以下两种情况。

①若本地载波用cosωc t,则得(为计算简便起见,略去发送端幅度1/2)

低通滤波器滤出cosΩt,即恢复cosΩt项。

②若本地载波用sinωc t,则得(为计算简便起见,略去发送端幅度

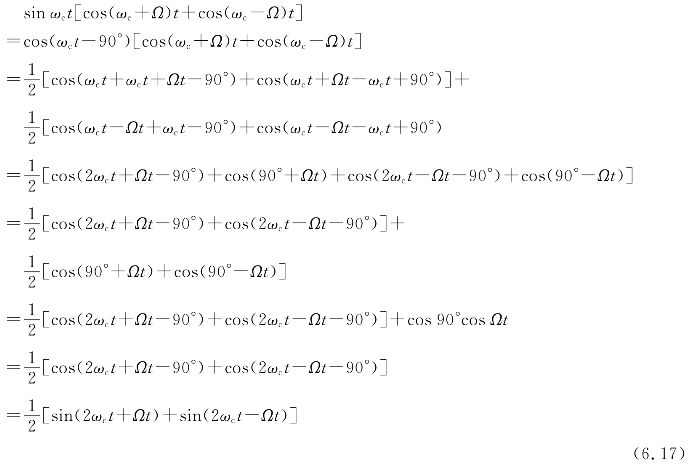
由式(6.17)可见,没有低频项,故低通滤波器输出为零。

由此得出结论:发送端用载波cosωc t时,接收端要对应本地载波为cosωc t才能有输出,若接收端对应的本地载波为sinωc t,则无输出。

同理,若发送端为sinωc t,接收端也分为以下两种情况。

①由(cosΩt sinωc t)sinωc t可推得,低通滤波器滤出cosΩt项,即恢复cosΩt项。

②由(cosΩt sinωc t)cosωc t可推得,低通滤波器无输出。

由此得出结论:发送端用载波sinωc t时,接收端要对应用载波sinωc t才能有输出,若用本地载波cosωc t,则无输出。

另外,同理,若再以S(t)信号的等其他项作为输入分析,也可得到一样的结果。

由此可见,两路信号合成(相加)传送与接收的过程如图6.44所示。

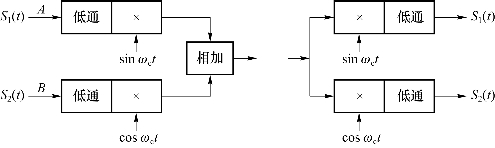
图6.44 两路信号合成(相加)传送与接收

可见A路发时只有A路收到,B路发时只有B路收到,在同一信道上传送,互不干扰。因为这种调制采用两种载波(即cosωc t和sinωc t),这两种载波是相互正交的,所以它又称为正交调制(OAM)。

(2)4PSK的产生

这种数字正交调制用于数据传输时,让一个数据序列分成两路,两路同时传送,从而加快传输速度。具体方法是在发端加一串/并转换,收端则应是并/串转换,如A路是①,③,⑤,…位码元组成,B路是②,④,⑥,…位码元组成,如图6.45所示。

图6.45 发端和收端的串/并转换

4PSK的产生电路如图6.45所示。考虑发端的乘法器(倒接开关调制器)和用双极性码作控制。倒接开关调制器的工作原理已在前文分析过,即1码发正脉冲,使输出的是正载波(sinωc t和cosωc t),0码发负脉冲,使输出的是负载波(-sinωc t和-cosωc t)。A、B两路相加后产生的四种结果如下。

①若A、B两路都发1码,即AB=11,则两路合成为

②若A、B两路都发0码,即AB=00,则两路合成为

③若A路发0码,B路发1码,即AB=01时,则合成为

④若A路发1码,B路发0码,即AB=10时,则两路合成为

据此画出矢量图,如图6.46所示,虚线箭头表示参考相位(基准相位),对绝对相移而言,参考相位为载波的初相。

图6.46 矢量图(体系)

图6.46中的双极性码与相角对应关系如表6.1所示。

表6.1 双极性码与相角对应关系

由图6.45所示的4PSK所产生的正交调制的四种不同状态(即四种不同相位的信号),属于四进制。根据四进制码与二进制码的关系可知,每一相位的信号包含2 bit信息。(www.xing528.com)

可见,为提高传信率Rb=RB log2 N,利用载波的一种相位去携带一组二进制信息码。

图6.46是按sin(ωc t+φ)来定的,其中φ=45°+n×90°(n=0,1,2,3)。我们把这个矢量图6.46称为是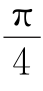体系的。

注意,一般画波形是根据sin(ωc t+φ)来画的,但在说明原理时常使用cos(ωc t+φ)来表示相移信号。

【例6.2】 画出数字序列101100100100的4PSK的体系波形图。

解:4PSK波形图如图6.47所示。

图6.47 4PSK波形图

注意:S(t)的一个四进码元时间Tb对应二位二进制码。

(3)4PSK的鉴相解调法(极性比较法)

4PSK的鉴相解调法如图6.48所示。

图6.48 4PSK的鉴相解调法

一个四相调相信号可以表示为sin(ωc t+φ),φ为已调波起始相位,有四种取值。

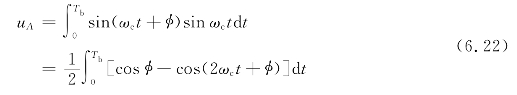
Tb为双比特码元周期(如图6.47所示),故在t=Tb时有

假设在t=Tb时刻进行抽样判决,那么式(6.22)的-cos(2ωc t+φ)d t项等于零。这是由于在持续时间Tb内有整数个余弦载波周期,所以其积分结果必为零。同理有

由上可见,A路积分输出与cosφ成正比,B路积分输出与sinφ成正比。sinφ和cosφ或为正(“+”)或为负(“-”)值,最终值经判决器后输出。判决准则:“+”值判为1,“-”值判为0,如表6.2所示。

表6.2 相角对应判决值

得到AB后,再恢复成原二位二进制码串行序列。

【例6.3】 数字消息分别为11,00,01,10时,试分析图6.49所示的4PSK输出相位矢量图。

图6.49 4PSK产生框图

解:AB=11时,合成输出为

AB=00时,合成输出为

AB=01时,合成输出为

AB=10时,合成输出为

据此画出的4PSK输出相位矢量图如图6.50所示,是按sin(ωc t+φ)来定的,其中φ=n×90°(n=0,1,2,3)。我们把这个矢量图称为是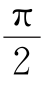体系的。

图6.50 矢量图(体系)

5.四相差分移相键控(4DPSK)

(1)规则

每一个四进制码元(二位二进制码元)载波与前一个四进制码元(二位二进制码元)载波有四种不同的相位差,即Δφ=φn-φn-1可得到四种不同的移相信号。四进制码元(二位二进制码元)的相对相移信号相位是将前一个四进制码元(二位二进制码元)的相位φn-1与Δφ相加。

(2)体系的4DPSK

①4DPSK产生框图如图6.51所示。

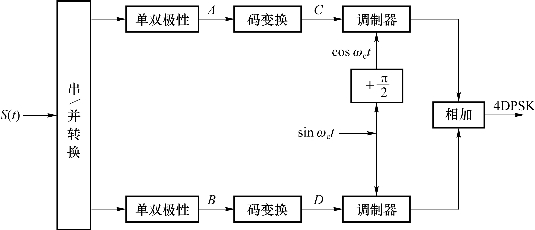
图6.51 4DPSK产生框图(体系)

它产生的矢量图如图6.52所示,是体系的。对差分相移而言,参考相位为前一个已调载波码元的末相(当载波频率是码元速率的整数倍时,也可认为是初相)。

图6.52的矢量图表示一种差分四相键控的信号组。坐标右模轴表示前一个四进码元的信号相位。例如,二位二进制码元“11”这一四进码元的差分移相信号的相位,将为前一四进码元的信号相位加Δφ=45°,其他类推,见表6.3所示。

表6.3 四进码元对应相位

②4PPSK相干解调框图如图6.53所示。

图6.53 4DPSK相干解调框图(体系)

收端不需要本地振荡器,而采用延迟线,使接收信号延迟一个四进制码元时间,成为前一个四进制码元的移相信号,接收信号与前一码元信号进入A路鉴相器。

同理

得到输出与cos(φn-φn-1)=cosΔφ成比例。接收信号经90°相移得到后,再进入B路鉴相器,于是输出与sin(φn-φn-1)=sinΔφ成比例。两路取样判决得到“+”“-”,经取样判决后得到表6.4所示的结果,再经过码变换及并/串变换后恢复为S(t)。

表6.4 相角对应判决值

4DSK与4PSK相干解调法不同之处在于,它是利用前一个载波相位作为参考相位进行解调的。延迟时间Tb为双比特码元(四进制码元)周期。这种电路结构比较简单,但误码性能较差。

③下面介绍体系的4DPSK调制波形图。体系的码元“11”对应的φn=45°+φn-1,其他四进制码元与体系载波相位的对应关系如表6.5所示。

表6.5 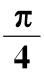体系载波相位与四进制码元的对应关系

根据规则,画出4DPSK的体系波形图,如图6.54所示。

图6.54 4DPSK的系波形图

(3)体系的4DPSK

①体系的4DPSK产生框图如图6.55所示。它产生的矢量图如图6.56所示,是体系的。

图6.55 4DPSK产生框图

图6.56 4DPSK矢量图

②4DPSK解调框图如图6.57所示。

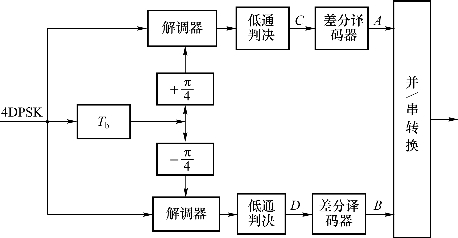
图6.57 4DPSK解调框图

C路接收为

D路接收为

接收信号sin(ωc t+φn)经过延迟线得到前一码元信号后,分别经过-45°和45°相移,成为sin(ωc t+φn-1-45°)和sin(ωc t+φn-1+45°),两者分别加至A路和B路的解调器(鉴相器)中,它们的输出分别与cos(Δφ-45°)和cos(Δφ+45°)成比例,如表6.6所示。

表6.6 相角对应判决值

【例6.4】 四相调制系统输入的二进制码元速率为4 800 baud,载波频率为2 400 Hz,已知数字与相位的对应关系为“00”↔0°,“01”↔90°,“11”↔180°,“10”↔270°。当输入码序列为011001110100时,试画出4PSK、4DPSK的信号波形图。

解:

画出的4PSK、4DPSK的信号波形图如图6.58所示。

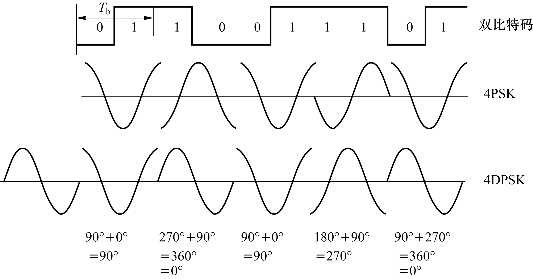
图6.58 4PSK、4DPSK的信号波形图

6.多相调制的星座图

多相调制也称多元调相,有二相、四相、八相、十六相、三十二相、六十四相等调制,它以载波的M种相位代表M种不同的数字信息。图6.59画出了二相、四相、八相调制的相位矢量图。

图6.59 多相调制的相位矢量图

例如,四相调制用载波的四种相位(起始相位)与两位二进制信息码(AB)的组合(00,01,11,10)对应,括号内的AB码组称为双比特码。若在载波的一个周期(2π)内均匀地分配四种相位,可有两种方式,即(0,π/2,π,3π/2)和(π/4,3π/4,5π/4,7π/4)。因此,四相调制的电路与这两种方式对应,就有π/2调制系统和π/4调制系统之分。

用矢量表示各相移信号时,其相位偏移有两种形式。图6.60所示的就是相位配置的两种形式。图中注明了各相位状态所代表的k比特码元,虚线为基准位(参考相位)。各相位值都是对参考相位而言的,正为超前,负为滞后。两种相位配置形式都采用等间隔的相位差来区分相位状态。

图6.60 相位配置矢量图

信号矢量端点的分布图称为星座图。例如,四相、八相信号矢量端点的分布图如图6.61所示。

图6.61 4相、8相的星座图

采用16PSK时,其星座图如图6.62(a)所示。若采用振幅与相位相结合的16个信号点的调制,两种可能的星座分别如图6.62(b)、图6.62(c)所示。其中,图6.62(b)为正交振幅调制,记作16QAM;图6.60(c)是话路频带(300～3 400 Hz)内传送9 600 bit/s的一种国际标准星座图,常记作16APK。

图6.62 16PSK、16QAM和16APK的星座图

7.交错正交相移键控(QPSK)

QPSK信号相位每相隔2Tb,相位跳变量可能为±90°或±180°,如图6.63中的箭头所示。

图6.63 QPSK相位跳变图

当码组从“00”↔“11”,“01”↔“10”对角移动时,会产生180°的载波相位跳变,而这种相位跳变会引起包络起伏,如图6.64所示。

图6.64 QPSK的相位跳变情况

滤波后其包络的最大值与最小值之比为无穷大,当通过非线性器件后,会使已滤波的频带外分量又被恢复出来,导致频谱扩展,增加对邻道的干扰。为消除载波180°的相位跳变,在QPSK基础上提出了OQPSK方式,OQPSK方式又称为一种恒包络数字调制方式。

OQPSK与QPSK不同点在于OQPSK将两支路上的码流在时间上错开一个Tb时间,不会发生两支路码元同时翻转的现象,每次只有一路可能发生极性翻转。这样相位只能是跳变0°或±90°,即只能沿正方形的四个边移动,如图6.65所示。

图6.65 OQPSK相位跳变图示意图

OQPSK的产生与解调分别解释如下。

①OQPSK产生框图如图6.66所示。

图6.66 OQPSK产生框图

延时电路Tb保证I、Q两路码元能偏移Tb。LPF是低通滤波器,BPF是带通滤波器。I、Q两路信号经过低通滤波器调制、合成,再通过带通滤波器后形成OQPSK信号,这个信号保持包络恒定。OQPSK信号的调制示意图如图6.67所示。

图6.67 OQPSK信号的调制示意图

②OQPSK解调电路如图6.68所示。

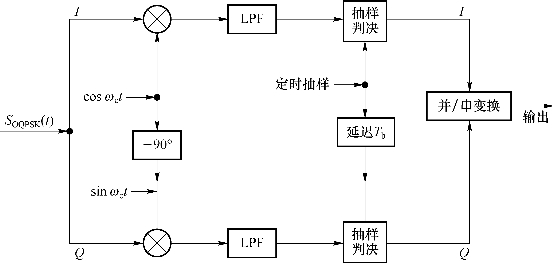
图6.68 OQPSK解调电路

8.QPSK

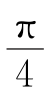QPSK的相位变化限于±45°、±135°,而QPSK是±180°、±90°,OQPSK是±90°,因此,QPSK保持恒定的性能比QPSK好,比OQPSK差。QPSK是对QPSK方式进行改进的另一种四进制调制方式:改进之一,将QPSK的±180°降为±135°;改进之二,QPSK只能相干解调,而QPSK即可相干解调,又可非相干解调,这将大大简化接收机的设计。在多径扩展和衰落的情况下,QPSK工作性能也要优于OQPSK。通常载波恢复存在一定相位模糊,QPSK会发生四相模糊性,从而造成大的误码率。为消除这一相位模糊性,QPSK在调制器内加差分编码器,在解调中加差分译码器,其电路如图6.69所示。

图6.69 QPSK产生框图

QPSK相位均匀等分为8个相位点,分成“”和“”两组,相位只能在两组之间交替选择,相位跳变必定在它们之间跳变,这样就使得码元转换时刻的相位突跳只可能出现±45°和±135°的情形,如图6.70所示。

图6.70 QPSK相位跳变图

QPSK已用于美国的IS-136数字蜂窝通信系统和个人接入通信系统(PCS)中。