数字基带信号传输的基本准则

数字信号(二进制)只有离散的两个幅度,其中低电平用0表示,而高电平用1表示,因此对数字信号传输的检测只需识别所传输数字信号的离散幅度值而不需要识别是何种波形。对于数字信号传输可采用在规定时刻抽样判决的方法对传输信号进行检测判决。通过适当地选择信号传输速率与传输频带,并采用抽样判决的方式,就可以实现符号间干扰为最小的数字信号传输。

图5.7(b)很重要,它表示窄脉冲传输经过矩形的信道时,接收端出现形的波形,每隔一定时间出现零点。这个波形图的重要性在于它表明,如果每隔时间(常称奈氏时段)发送数据脉冲,不管发0码或者1码,只要准确地按照这种间隔时间发送脉冲。就不会发生码间干扰(即符号间干扰),因为这一位码(符号)的接收波形峰值正是前后码(符号)的零点。

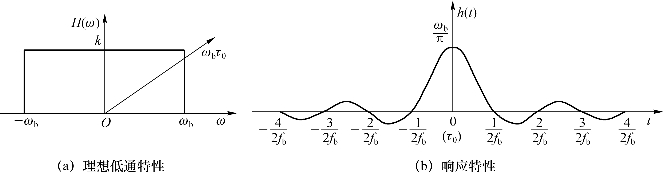
图5.7 基带传输系统的理想低通特性和响应特性

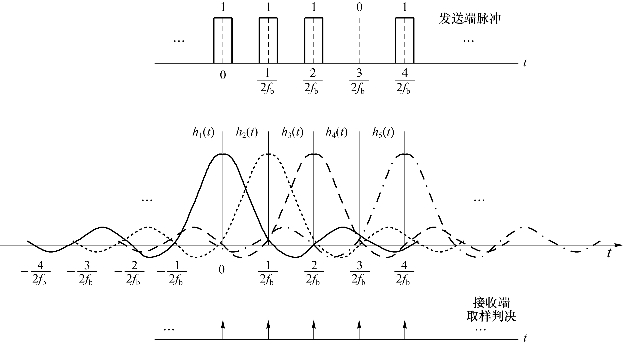
不过,应该注意图5.8所示的波形频谱,在这种矩形频谱所产生的形时间响应中第一个零点以后的尾巴振荡较为剧烈,振荡幅度较大,这意味着,发送端发出脉冲的间隔时间必须很准确,接收端取样判决时间也必须很准确,低通滤波特性载止频率fH必须很稳定。就是说,对三个条件的要求都很严格,稍差一点就可能引起码间干扰,这就是矩形频谱的缺点。

(www.xing528.com)

图5.8 最大值点处抽样判决示意图

同时,从图5.8可以看出,邻近脉冲的间隔时间为也就是,每秒传送2fb个码元,即码速等于2fb,而fb为低通滤波器的截止频率,这意味着,信道如果有理想的矩形频谱,则频带每赫兹传送信息的速率可以达到2 bit/s/Hz,这是频谱的优点。

例如,低通滤波器的截止频率fb=4 k Hz,发送脉冲的间隔时间为如为二进制脉冲,每个脉冲有1 bit信息,每秒就传送信息8 kbit。在4 k Hz带宽内传送信息8 kbit,就是每赫兹传送信息2 bit/s/Hz。

从图5.8可以看出,当传输的脉冲序列满足的条件,或者说以2fb(fb是等效理想低通滤波器的截止频率)的速率发送脉冲序列时,在输出响应的最大点处的数值仅由发射端脉冲所决定,因此,在最大值点处进行抽样判决就可以消除符号间干扰了。图5.8所示的就是以2fb的速率发送脉冲序列11101…时的情况。

由此可见,当满足传输速率是2fb,而信道带宽是fb时,就可以做到没有符号间干扰的传输,这一关系就是数字信号传输的一个重要准则——奈奎斯特第一准则。其含义是当数字信号序列通过某一信道传输时,码元响应的最大值处不产生符号间干扰的极限速率是2fb,这时的传输效率是2 bit/s/Hz。根据奈奎斯特第一准则,在理想情况下传输数字信号所要求的带宽是所传数字信号速率的一半。例如,传输速率为2.048 Mbit/s的数字信号在理想情况下要求最小的通路带宽是1.024 MHz。