均匀量化有一个很大的缺点,即量化信噪比随信号电平的减小显著下降,也就是说,当信号很大时,其信噪比比平均信噪比大,这是有利的,而当信号很小时,其信噪比比平均信噪比小很多。音量小的信号本来听起来就费劲,再在加上信噪比低,信号问题将更严重。
例如,Vm=128 m V,n=7,则![]() 。
。
那么量化平均信噪比为
![]()
当为大信号128 m V时,信噪比为

而当为小信号1 m V时,信噪比为
![]()
以上u噪声均取![]() m V,由此可见,小信号的信噪比远小于平均信噪比。改善措施是增加分层数,例如,把n由7改为9,Vm=128 m V,那么
m V,由此可见,小信号的信噪比远小于平均信噪比。改善措施是增加分层数,例如,把n由7改为9,Vm=128 m V,那么

这时
![]()
可见,当小信号为1 V时,信噪比为20lg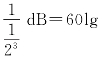 2 dB≈18 dB,这样信噪比就大大提高了。
2 dB≈18 dB,这样信噪比就大大提高了。
但是,不能无限增加码元数n,因为总的码元速率(系统)提高,小信号编码精度不易保证,设备制造烦琐,需更宽的信道频带。解决思路是采取相应弥补措施,即降低大信号的信噪比来换取小信号信噪比的提高,具体做法有两种。
第一种方法是先用压缩器对信号进行非线性压缩,非线性压缩指对大、小信号分别进行不同程度的放大,改变大小信号间的差异。线性压缩是指对大、小信号放大程度一致。

第一种方法的特点是在发送端对输入量化器前的信号进行压缩处理,在接收端再进行相应的扩张处理,如图3.13(a)所示,信号压缩和扩张的结果示意图如图3.13(b)所示。

图3.13 非均匀量化压扩特性原理
由图3.13可见,输入信号中幅值小的信号在压缩后幅值变大,而幅值大的信号经压缩后变小,这种输入和输出信号之间的关系是非线性的,它改变了大信号与小信号之间的比例关系,使得对大信号的增益基本不变或改变很小,而对小信号相应地按比例放大。这种经过压缩处理后的信号再进行均匀量化,最后的等效效果就是对原信号进行非线性量化。
在图3.13中,均匀量化电平为8级。一个输入信号样值脉冲在压缩前均匀量化时量化为1 m V,而在压缩特性处理后量化为5 m V,可见小信号电平明显增大,从而使信噪比增加。原来小信号1 m V的信噪比为![]() dB≈6 dB,经压缩特性处理后小信号变为5 m V,此时的信噪比为20lg
dB≈6 dB,经压缩特性处理后小信号变为5 m V,此时的信噪比为20lg![]() dB=20lg 10 dB=20 dB。而大信号在脉冲压缩前后电平变化很小,信噪比也基本没变化。
dB=20lg 10 dB=20 dB。而大信号在脉冲压缩前后电平变化很小,信噪比也基本没变化。
第二种方法是在总分层数不变情况下,对小信号分层加密,对大信号分层相对扩疏。这样量阶值Δk是个变值,小信号分层多,Δk小,于是![]() 相应减小,从而提高信噪比,而大信号分层多,误差相对大。这种方法称为非均匀量化法。
相应减小,从而提高信噪比,而大信号分层多,误差相对大。这种方法称为非均匀量化法。
第一种方法的应用实例是A律压缩曲线,即
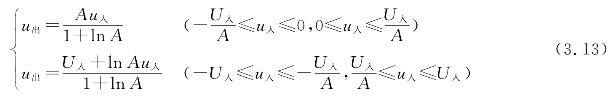
其中,A是一常数,称为压缩参数;U入为u入的最大值。根据式(3.14)得图3.14所示的A律压缩曲线。

图3.14 A律压缩曲线
如果设u出最大输出电压为U出,且设![]() 式(3.14)两边及其定义域同乘
式(3.14)两边及其定义域同乘![]() 可得
可得

其中![]() 项修正后为
项修正后为![]() 项。故得
项。故得

令![]() 则得
则得
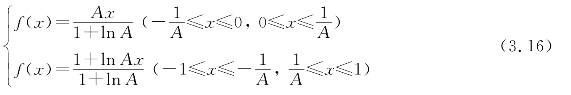 (https://www.xing528.com)
(https://www.xing528.com)
根据式(3.17)作出归一化A律压缩曲线(如图3.15所示)。

图3.15 归一化A律压缩曲线
在接收端对应扩展特性如图3.16所示。

图3.16 归一化扩展特性
在归一化A律压缩曲线中,在0~1/A和-1/A~0范围内为低电平压,并且f(x)对应是一段直线,即线性函数。在1/A~1和-1~-1/A范围内为高电平压,并f(x)对应是一段曲线,即一对数函数。
取A=87.6,A=1,A=2,仅画出此时曲线的正特性部分,如图3.17所示。
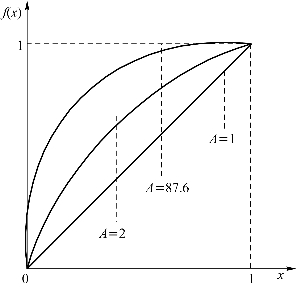
图3.17 A=1,A=2,A=87.6的各自正特性
实际证明A=87.6是最佳语音压缩(扩张)特性。由于我们要进行的是绝对值编码,所以只画正特性即可。
第二种方法的应用实例是A律压缩特性的13折线近似法,这是在使用第一种方法的基础上再应用叠加第二种方法,如图3.18所示。
A律压缩特性的13折线近似法的分段具体过程:x轴按 等比级数,把0~1划分成8个不均匀段并编号①~⑧,如图3.18(a)所示。对应y轴也划分为8个均匀段,如图3.18(b)所示,各曲线段(①~⑧)的斜率如下。
等比级数,把0~1划分成8个不均匀段并编号①~⑧,如图3.18(a)所示。对应y轴也划分为8个均匀段,如图3.18(b)所示,各曲线段(①~⑧)的斜率如下。

其中,①、②线段的斜率相同,两者同为一直线,负特性对称同样为8段曲线,若用上述①~⑧的斜率代替原有曲线,这样整条曲线(即正负特性)中有4条线段为同一直线。将所有线段合为一条直线的话,应用13条直线(斜率不同)段来近似代替原曲线,故称为13折线近似法。
再把①~⑧段各自再均匀划分成16个小段。例如,③段分成均匀16小段,如图3.19所示。这样x轴上共有8×16=128个不均匀分层,即有128个非均匀量化级数。可见,仍然是小信号量阶值小,大信号量阶值大,Δk是个变值。将①~⑧个大段划分为如下小段。
①段划分为16个均匀小段,每个小段长度为![]()

图3.18 A律压缩特性的13折线近似法示意图
②段划分为16个均匀小段,每个小段长度为![]() =Δ。
=Δ。
③段划分为16个均匀小段,每个小段长度为![]() =2Δ。
=2Δ。
④段划分为16个均匀小段,每个小段长度为![]() =4Δ。
=4Δ。
⑤段划分为16个均匀小段,每个小段长度为![]() =8Δ。
=8Δ。
⑥段划分为16个均匀小段,每个小段长度为![]() =16Δ。
=16Δ。
⑦段划分为16个均匀小段,每个小段长度为![]() =32Δ。
=32Δ。
⑧段划分为16个均匀小段,每个小段长度为![]() =64Δ。
=64Δ。

图3.19 ③段分成均匀16小段
如果把x轴做均匀量化处理,则均匀量化是以Δ作为一个小段,第①~②段就要划分成为16小段,第③段就要划分成32个小段〔如图3.20(a)所示〕,第④段就要划分成64个小段,…,第⑧段就要划分成1 024个小段。均匀量化时,8个段分成了2 048个Δ小段,如图3.20(b)所示。

图3.20 均匀量化时示意图
这样的话x轴共有(16+16+32+64+128+256+512+1 024)Δ=2048Δ小段。量化级数Q与二进制码位数关系为Q=2n,若令Δ=1,则2048=211。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




