均匀量化特性及其影响分析

1.量化

模拟信号x(t)经抽样后得到样值序列{x(n Ts)},虽在时间上离散了,但在幅度上取值却是连续的,即{x(n Ts)}可以有无限多种取值,这种样值无法用有限数值来表示,因此要把样值序列{x(n Ts)}做进一步处理,变成有限的幅度值,这个变成有限值的过程就是量化,如图3.6所示。

图3.6 样值序列{x(n Ts)}示意图

模拟抽样值{x(n Ts)}:

1.61 V -1.53 V 1.72 V 1.5 V 1.9 V 0.73 V

量化值(近似值):

1.5 V-1.5 V 1.5 V 1.5 V 2 V 1 V

量化值二进制码表示:

00 01 00 00 10 11

上例取的是-2～2 V间的任意值,而不是有限值,所以这还不能完全称为数字信号。

问题是,在实际通信系统中是不是一定要传输这个样点值的精确值呢?事实证明并不需要,只传输它的近似值就行,这就提出了量化的概念。

所谓量化,就是把抽样信号取得的任意值,用一个有限数值来近似代替的过程。

图3.6中的{x(n Ts)}={1.6 V,-1.5 V,1.7 V,1.5 V,1.9 V,0.7 V}是精确值,而{1.5 V,-1.5 V,1.5 V,1.5 V,2 V,1 V}是量化值。

均匀量化过程的例子如图3.7所示。

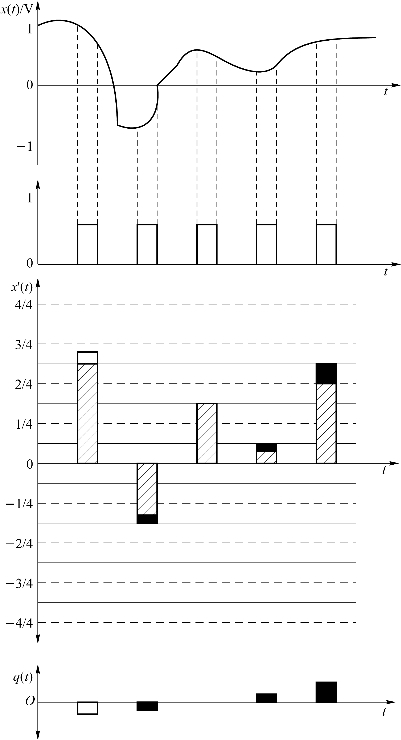
图3.7 均匀量化过程的例子

均匀量化步骤如下。

①把-1～1 V区间划成若干均匀等分,例如,将-1～1 V区间划分为8个均匀等分,即-1～-3/4 V,-3/4～-2/4,…,3/4～1。

②步骤①的目的是不精确传递任一x′(t)精确值,采用类似“四舍五入”的方法,把落入任一等分中的样点值都以这个等分中的中间值来代替。例如,当时,把x′(t)当作5/8;若把x′(t)当作-3/8。

③当信号绝对值大于一级中间值时,舍弃“零头”;当信号绝对值小于中间值时,就补足“零头”,这样可取-7/8,-5/8,-3/8,-1/8,1/8,3/8,5/8,7/8八个数值之一,这个过程称为量化。

量化过程如图3.8所示,用量化后的信号xq替代取样信号x′(t)。

图3.8 量化过程

上例的8个量化数值可用一位十进制数字代表,也可化为三位二进制(23=8)数。

2.均匀量化特性分析

在图3.7中的8个等级量化是等间隔量化,称作均匀量化,上例均匀量化过程也可用图3.9(a)表示,此图称为均匀量化特性曲线,而图3.9(b)称为均匀量化误差曲线。

图3.9 均匀量化特性曲线与误差曲线图

均匀量化间隔称为阶梯值Δk,阶梯值也称为级差。在上例中,信号在-1～1 V之间的阶梯值,那么级差就是1/4 V。xq与x的关系形成等距阶梯,两者之间存在的误差就是量化误差,用q=xq-x表示,两级交界点误差最大为在之间。误差曲线对应的函数式如式(3.4)所示。(www.xing528.com)

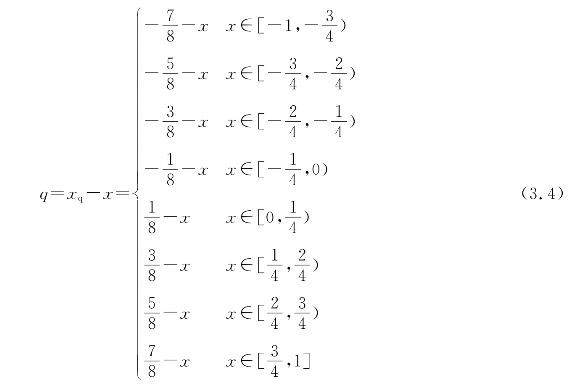
如图3.10所示,一般地说,设量化级数为Q(Q=1,2,…,K),共有2n个级量化值。K=1为第1级量化值(从-V算起),K=Q为第Q级量化值。

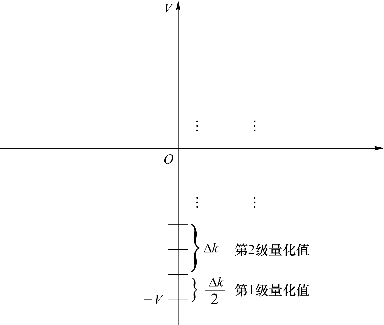
图3.10 量化级数示意图

上述例中可有如下量化级数(量化电平数):第1量化级-1≤x′(t)＜-第2量化级第3量化级;第4量化级;第5量化级0≤x′(t)＜;第6量化级;第7量化级;第8量化级≤x′(t)≤1。

上述例子的8个等级量化有8个量化值,如果用二进制码表示,则每个量化值需用三位代码构成三元码组,因为23=8。

以上分层规律可一般化,即每个量化值相应的二进制码元位数为n,则量化级数Q=2n。

若设取样信号x′(t)的电平变化范围在-V～+V之间,则阶梯值,Q=2n。最大量化误差为例如,n=3,23=8,V=1 V,则。再例如,n=7,27=128,V=64 V,则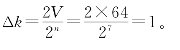

若设取样值x′(t)的电平变化范围在0～Vm之间,则阶梯值最大量化误差为例如,Vm=8,n=3,则

【例3.1】 对频率为0～300 Hz的模拟信号,求最低抽样频率fs,若量化电平数Q=64,求信息传输速率Rb。

解:该信号的低通型信号由抽样定理得

fs=2fH=2×300=600 Hz

量化的电平编成二进制码元,则Q=2n。

由64=26可知,每个抽样值将被编成6位二进制码。

RB2=nfs=6×600=3 600 baud

Rb2=RB2

Rb2=3 600 bit/s

【例3.2】 已知正弦信号为3.25sin(2πft)V,将它输入一个均匀量化器中,其量化特性如图3.11所示,画出输入为正弦波时的输出波形。(假设抽样频率fs=8 k Hz,正弦信号频率f=800 Hz)。

图3.11 量化特性

解:正弦信号为x(t)=3.25sin(2π×800×t)V=3.25sin(1 600πt)V,抽样周期为则

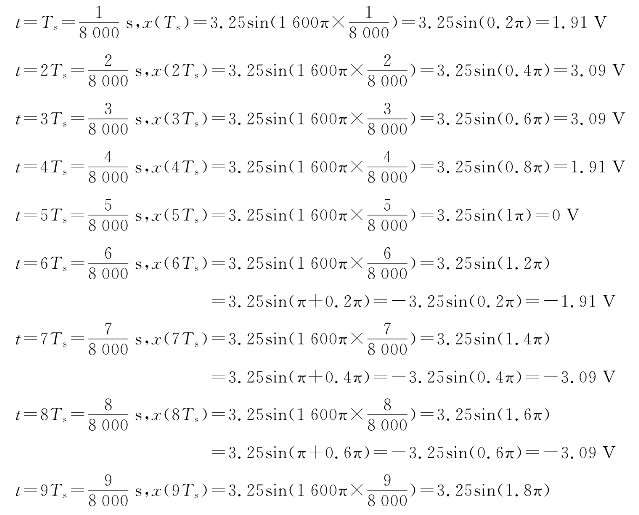
画出的输出波形如图3.12所示。

图3.12 例3.2的输出波形

3.均匀量化的量化信噪比

量化信噪比是衡量量化性能的指标,量化误差大,对重建信号有很坏的影响。量化信噪比为

均匀量化时其量化信噪比随信号电平的减小而下降,产生这一现象的原因是均匀量化时的量化级间隔Δ为固定值,而量化误差不管输入信号的大小均在(-Δ/2,Δ/2)内变化。故大信号时量化信噪比大,小信号时量化信噪比小。对于语音信号来说,小信号出现的概率要大于大信号出现的概率,这就使平均量化信噪比下降。同时,为了满足一定的量化信噪比输出要求,要改善小信号量化信噪比,可以采用量化间隔非均匀的方法,即非均匀量化。